双连续n次积分C余弦函数的概率逼近

岳田，雷国梁

（湖北汽车工业学院理学院，湖北十堰442002）

双连续n次积分C余弦函数的概率逼近

岳田，雷国梁

（湖北汽车工业学院理学院，湖北十堰442002）

利用双连续n次积分C余弦函数与双连续n次积分C半群之间的关系，借助于双连续n次积分C半群的Taylor公式，得到了双连续n次积分C余弦函数的Taylor展式，然后借助于概率论的方法及算子值数学期望等工具，给出了双连续n次积分C余弦函数概率型逼近表达式。

双连续n次积分C余弦函数；Taylor展开式；率型逼近

随着算子半群相关理论的发展，余弦算子函数的研究也一直为人们所关注，产生了许多重要的研究结果［1-8］。如文献［1］中引入了指数有界的C余弦算子函数的生成元，讨论了其相关性质，并建立了相应的生成、逼近及扰动定理；文献［2］利用生成元的预解式来刻画了m次积分余弦函数的逼近性质；文献［3］利用指数有界C余弦算子函数的性质并借助概率相关理论，给出了指数有界C余弦算子函数的概率逼近公式及Vonorovskaya型渐近公式；文献［4］中作者引入一致双连续半群的概念，借助Laplace变换和Trotter-Kato定理，得到了双连续n次积分C余弦函数的逼近定理；文献［6-7］分别利用与C余弦函数及α次积分C余弦函数相关的抽象Cauchy问题对其生成元的性质进行了细致的讨论。文献［9］在Banach空间上附加了一个比范数拓扑粗的局部凸拓扑，使得半群在该局部凸拓扑下强连续，由此提出了双连续半群概念，为半群理论开辟了新的研究领域。文献［10］中分析了局部凸拓扑下的Riemann-Stieltjes积分，给出了双连续半群的逼近定理及其应用。借助概率论这一重要工具，将半群理论与逼近理论相结合，来解决算子半群的逼近问题，并在很大程度上为其提供了收敛速度的精确估计式。如文献［11-12］给出了双连续C半群概率逼近的Chernoff乘积公式、指数公式、Vo⁃norovskaya型渐近公式等若干渐近公式。

文中以双连续n次积分C余弦函数与双连续n次积分C半群之间关系为基础，借助于双连续n次积分C半群的Taylor公式，给出了双连续n次积分C余弦函数的Taylor公式，从而得到了双连续n次积分C余弦函数的概率型逼近式。

1　相关定义及引理

对双连续n次积分C余弦函数所在的空间作如下约定：设（X，‖∙‖）是Banach空间，其共轭空间为X′，τ是X上的一个局部凸拓扑并具有如下性质：

1）空间（X，τ）在‖∙‖-有界集上序列完备；

2）拓扑 τ比拓扑‖∙‖-粗且 τ是Hausdorff拓扑；

3）空间（X，‖∙‖）中的范数可由空间（X，τ）′定义，即对每个x∈X，有

为方便起见，记

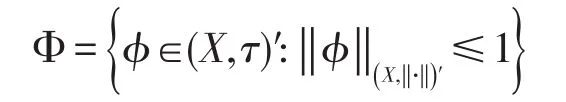
文中所有算子均为线性算子，D（A）为算子的定义域，L（X）为X到自身的有界线性算子全体，算子C∈L（X）为单射，NBV［0，T］是定义在［0，T］上的普通函数，NBVloc:=⋂T＞0NBV［0，T］，所有积分均是在τ-拓扑意义下的Riemann-Stieltjes积分。

定义1［10］X是局部凸拓扑τ的Banach空间，α∈NBV［0，R］，函数 f:［0，R］↦X是Rie⁃mann-Stieltjes可积的，如果

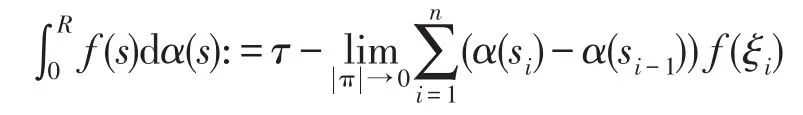
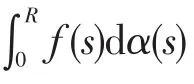
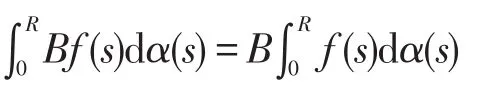
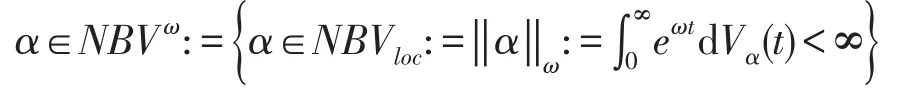
是（X，‖∙‖）上的有界线性算子。进一步地，若B:（X，τ）↦（X，τ）是线性τ-连续的，则

定义2［9］称算子T∈L（）X双连续，如果对每个‖∙‖-有界序列（xn）n∈N⊆X，且

定义4［4］称C（t）t≥0⊆B（X）为指数有界双连续n次积分C余弦函数（记Gnτ（M，ω，C）），如果满足：

1） C（0）=0，且

2）C（t）C=CC（t）；

3）C（t）x=0，蕴含着x=0，∀t≥0，x∈X；

4）C（t）t≥0强τ-连续；

5）C（t）t≥0局部等度双连续；

6）C（t）t≥0指数有界，即 ∃M，ω≥0，使得‖C（t）‖≤Meωt，∀t≥0；

由上述定义及引理给出定义：

是（X，‖∙‖）上的有界线性算子。进一步地，若B:（X，τ）↦（X，τ）是线性τ-连续的，则

由定义，E［C（t）］显然满足:

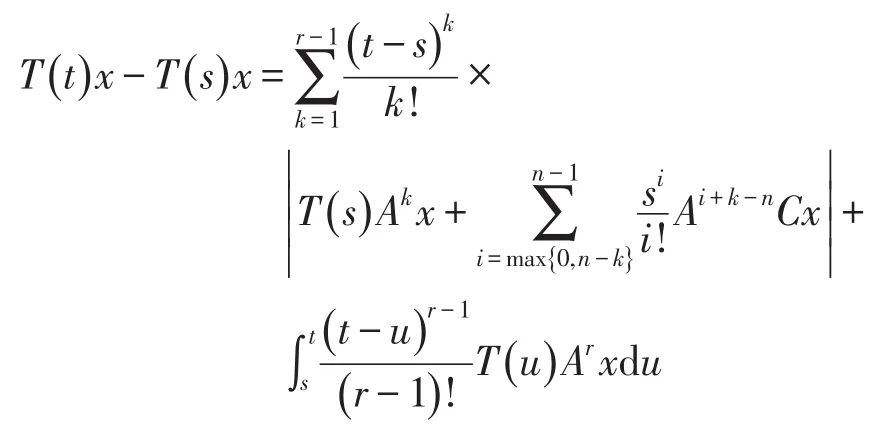
引理4［13］设B是双连续n次积分C余弦函数C（t）的无穷小生成元，B=A2。若x∈D（Ar），r≥1，则有

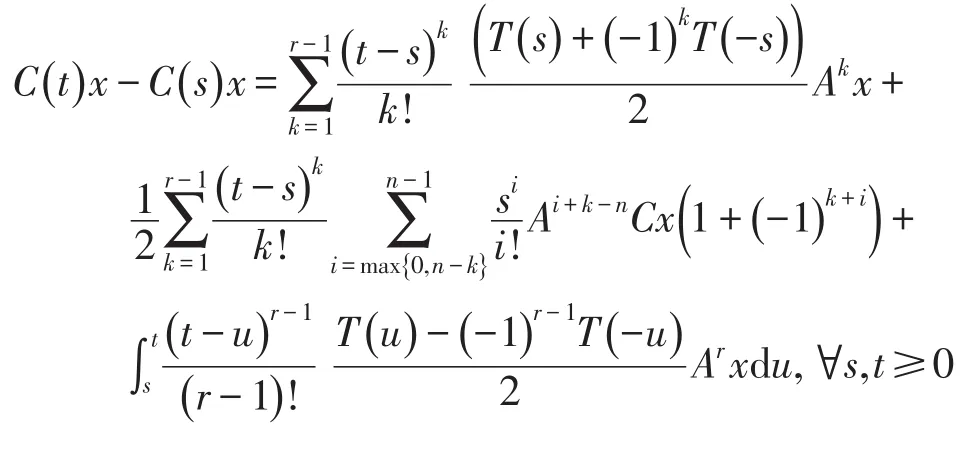
2　双连续n次积分C余弦函数的概率逼近

定理1设B是双连续n次积分C余弦函数C（t）的无穷小生成元，B=A2，U是非负实值随机

证明当x∈D（B ）时，在定理1中令r=1，t=U，s=ξ，两边取期望并利用H¨lder不等式，则有

［1］郑权，雷岩松.指数有界的C余弦算子函数［J］.系统科学与数学，1996，16（3）：242-252.

［2］曹德侠，宋晓秋，张祥芝.m次积分余弦算子函数的逼近［J］.数学的实践与认识，2007，37（9）：164-167.

［3］赵月英，宋晓秋.指数有界C余弦算子函数的概率型表示［J］.山东大学学报：理学版，2010，45（4）：77-81.

［4］李慧敏，宋晓秋，赵月英，等.双连续n次积分C余弦函数的逼近定理［J］.应用泛函分析学报，2010，12（3）：249-253.

［5］李慧敏，宋晓秋，赵月英，等.双连续α次积分C余弦函数的生成定理［J］.中国矿业大学学报，2010，39（3）：465-470.

［6］Kuo C C，Shaw S Y.C-Cosine functions and the Abstract Cauchy Problem，Ⅰ［J］.J.Math.Anal.Appl.，1997，210: 632-646.

［7］Kuo C C.Onα-times Integrated C-cosine Functions and Abstract Cauchy ProblemⅠ［J］.J.Math.Anal.Ap⁃pl.，2006，313:142-162.

［8］WANG M，XU F.α-times Integrated Cosine Operator Functions with Growthω［J］.Chin.Quart.J.Math.，2011，26（2）:229-233.

［9］KUHNEMUND F.A Hille-Yosida Theorem for Bi-contin⁃uous Semigroups［J］.Semigroup forum，2003，67（2）:205-225.

［10］JARA P.Rational Approximation Schemes for Bi-contin⁃uous Semigroups［J］.J.Math.Anal.Appl.，2008，344：956-968.

［11］赵月英，宋晓秋，李慧敏，等.双连续C半群的概率逼近［J］.中国矿业大学学报，2010，39（6）：941-946.

［12］岳田，宋晓秋.双连续C半群概率表示的渐近公式［J］.中国矿业大学学报，2013，42（5）：893-898.

［13］周玮，宋晓秋，李晓敏.n次积分C余弦函数的概率型逼近问题［J］.徐州师范大学学报：自然科学版，2008，26（4）：31-34.

Probabilistic Approximations for Bi-continuous n-times Integrated C-cosine Functions

Yue Tian，Lei Guoliang
（School of Sciences，Hubei University of Automotive Technology，Shiyan 442002，China）

Based on the relationship of bi-continuous n-times integrated C-consine function and bicontinuous n-times integrated C-semigroups，and with the Taylor formula of Bi-continuous n-times in⁃tegrated C-semigroups，the Taylor formula was presented for Bi-continuous n-times integrated C-con⁃sine functions.By means of the probability theory and operator-valued mathtmatical expectation，the probabilistic approximation for Bi-continuous n-times integrated C-consine function was given.

bi-continuous n-times integrated C-cosine functions；Taylor expansion formula；probabi⁃listic approximation

O177.2

A

1008-5483（2015）04-0062-04

10.3969/j.issn.1008-5483.2015.04.015

2015-05-15

中央高校基本科研业务费专项资金（2012LWB53）

岳田（1988-），男，四川南江人，硕士，主要从事应用泛函分析方面的研究。E-mail：ytcumt@163.com