“动态问题”求解探究

冯永乐

[摘 要]

动态问题变化形式多样，综合性强，教学中教师应抓住数形结合思想和分类讨论思想，揭示变量与变量，变量与不变量之间的关系，让学生学会解决动态问题。

[关键词]

动态问题;数形结合;分类讨论

动态问题是应用数学中的一个重要的部分，其变化形式多样，根据不同的变化情况可归纳为动点、动线、动形三种类型。它的综合性强，是对学生的综合能力、思维能力、创新能力的综合考查，在考试中常以压轴题的形式出现。因为这类问题思维跨度大，而且还需要有动与静的辩证思考等等，学生觉得难度大。因此要让学生掌握，就应教给学生解决问题的思想方法，采用“动静结合，以静制动”等思维方法，揭示变量与变量，变量与不变量之间的关系，揭示动态问题背后蕴含着核心的数学思想——数形结合思想和分类讨论思想，从而达到掌握解题思路及探究方法。

一、动点问题

（一）动点形成函数问题

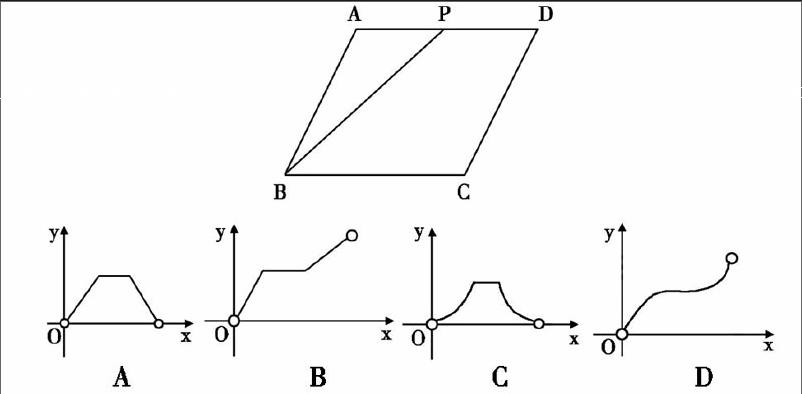
例1.如图，点P是□ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是（ ）。

分析：分三段来考虑点P沿A→D运动，△BAP的面积逐渐变大;点P沿D→C移动，△BAP的面积不变;点P沿C→B的路径移动，△BAP的面积逐渐减小，据此选择即可。

本题主要考查了动点问题的函数图象，注意分段考虑。解决问题的关键在于利用画图，结合分类讨论思想，将问题分解成几个“静态”问题，由“动”转化为“静”求解。

（二）动点形成最值问题

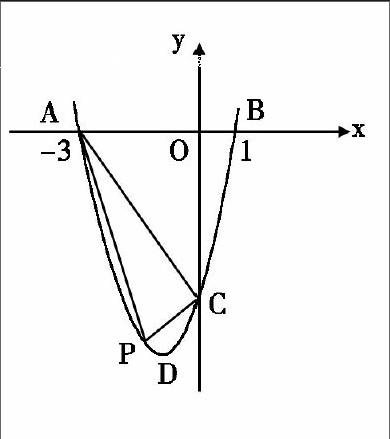
例2.二次函数y=ax2+bx+c（a≠0）的图象与x轴的交点为A（-3，0）、B（1，0）两点，与y轴交于点C（0，-3m）（其中m>0），顶点为D。

（1）求该二次函数的解析式（系数用含m的代数式表示）;

（2）如图，当m=2时，点P为第三象限内的抛物线上的一个动点，设△APC的面积为S，试求出S与点P的横坐标x之间的函数关系式及S的最大值;

（3）分析：①利用交点式求出抛物线的解析式;

②先求出S的表达式，再根据二次函数的性质求出最值;

本题考查了函数的图象与性质、待定系数法、图形面积计算等知识点。第（2）问重点考查了图形面积的计算方法;运用数形结合、函数及方程思想是解题的关键。

（三）动点形成的存在性问题

例3.如图，二次函数y=x2+bx+c的图象与x轴交于A（3，0），B（-1，0），与y轴交于点C。若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动。

（1）求该二次函数的解析式及点C的坐标;

（2）当点P运动到B点时，点Q停止运动，这时，在x轴上是否存在点E，使得以A，E，Q为顶点的三角形为等腰三角形？若存在，请求出E点坐标;若不存在，请说明理由。

分析：①将A，B点坐标代入函数y=x2+bx+c中，求得b、c，进而可求解析式及C坐标。

②等腰三角形有三种情况，AE=EQ，AQ=EQ，AE=AQ。借助垂直平分线，画圆易得E大致位置，设边长为x，表示其他边后，利用勾股定理易得E坐标。

本题考查了二次函数性质、利用勾股定理解直角三角形等知识，运用数形结合、分类讨论及方程思想是解题的关键。

二、动线问题

例4.如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm。点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于E、F、H，当点P到达点C时，点P与直线m同时停止运动，设运动时间为t秒（t>0）。

（1）当t=2时，连接DE、DF，求证：四边形AEDF为菱形;

（2）在整个运动过程中，所形成的△PEF的面积存在最大值，当△PEF的面积最大时，求线段BP的长;

（3）是否存在某一时刻t，使△PEF为直角三角形？若存在，请求出此时刻t的值;若不存在，请说明理由。

分析：①如图1所示，可证明AE=ED=DF=FA;

②如图2所示，首先求出△PEF的面积的表达式，然后利用二次函数的性质求解;

③如图3所示，分三种情形，需要分类讨论，分别求解，其中第一种情况不存在。

本题是运动型综合题，涉及动点与动线两种运动类型。第（1）问考查了菱形的判别方法;第（2）问考查了相似三角形、图形面积及二次函数的极值;第（3）问考查了相似三角形、勾股定理、解方程等知识点，重点考查了分类讨论的数学思想。

三、动形问题

抓住变量与不变量，探索平移、旋转和翻折等几何图形变换的解决方法。

（一）几何图形的平移变换

例5.如图1所示，一张三角形纸片ABC，∠ACB=90°，AC=6，BC=8.沿斜边AB边上的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形.将纸片△AC1D1沿直线D2B（AB）方向平移（点A、D1、D2、B始终在同一直线上），当点D1与点B重合时，停止平移。在平移过程中，C1D1与BC2交于点E，AC1与C2D2、BC2分别交于点F、P。

（1）当△AC1D1平移到如图2所示的位置时，猜想图中的D1E与D2F的数量关系，并证明你的猜想;

（2）设平移距离D2D1为x，△AC1D1与△BC2D2重叠部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围;

（3）对于（2）中的结论是否存在这样的x的值，使重叠部分面积y等于原三角形ABC的面积的[14]，若存在，请求出x的值，若不存在，请说明理由。

抓住此图形在平移过程中的角的不变量，线段的不变量，用变量x表示D1E、BD1、D2F的长，利用相似三角形、方程思想和以静制动的思维方法是解题的关键。

（二）几何图形的旋转变换

例6.将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°;在Rt△DEF中，∠EDF=90°，∠E=45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C。

（1）求∠ADE的度数;

（2）如图②，将△DEF绕点D顺时针方向旋转角α（0°<α<60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试（下转第33页）（上接第19页）判断[PMCN]的值是否随着α的变化而变化？如果不变，请求出[PMCN]的值;反之，请说明理由。

分析：①根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD=[12]AB，根据等边三角形性质求出∠BDC=∠B=60°，再求出∠ADC=120°，再根据∠ADE=∠ADC-∠EDF计算即可得解;

②根据旋转变换的性质可得∠PDM=∠CDN，再根据然后求出△BCD是等边三角形，根据等边三角形的性质求出∠BCD=60°，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CPD=60°，从而得到∠CPD=∠BCD，再根据两组角对应相等，两三角形相似判断出△DPM和△DCN相似，再根据相似三角形对应边成比例可得[PMCN=PDCD]为定值。

本题考查了旋转变换的性质，直角三角形的性质，等边三角形的判定与性质，相似三角形的判定与性质等知识。解题的关键是注意数形结合思想与以静制动的思维方法的应用。

（三）几何图形的翻折变换

例7.矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为__________。

分析：①如图1，当∠EFC=90°时，且点F在对角线AC上，利用勾股定理列式求出AC，设BE=x，表示出CE=8-x，根据翻折变换的性质可得AF=AB=6，EF=BE=x，然后在Rt△CEF中，利用勾股定理列出方程求解可得BE=3;②如图2，当∠CEF=90°时，且点F在AD上，判断出四边形ABEF是正方形，根据正方形的四条边都相等可得BE=AB=6。

本题考查了翻折变化的性质，勾股定理，正方形的判定与性质，此类题目，利用勾股定理列出方程求解是常用的方法，本题难点在于分情况讨论，作出图形更形象直观。

在数学知识应用中，常常遇到关于图形变换问题的求解，就其变化方式而言，主要由点、线、面的变换而得出的问题求解。在解决问题的思维方式，即找出变与不变的关系，由动到静，由静想到动。此类问题的应用广泛，举不胜举。在学习和教学中要善于归纳小结，解决问题的思路，万变不离其宗，当然因其解题过程渗透数形结合、函数方程思想、分类讨论等重要的数学思想方法，因此，教师的教学应注重归纳，达到事半功倍的效果，培养和提高学生的数学解题能力。

[参 考 文 献]

[1]周冬琴.“图形运动问题”教学中难点的分析与突破[J].中小学数学，2013（12）.

[2]陈龙彬.谈谈初中数学“动态问题”的分析策略[J].中小学数学，2014（3）.

[3]卢海明.探析初中数学动态几何问题[J].福建中学数学，2014（1、2）.

（责任编辑：张华伟）