Scour depth beneath a pipeline undergoing forced vibration

Y.Lun，D.Ling∗，R.Rn

aDepartment of Engineering，University of Cambridge，Cambridge CB2 1PZ，UK

bMOE Key Laboratory of Hydrodynamics，Shanghai Jiao Tong University，Shanghai 200240，China

cSchool of Business and Economics，Loughborough University，Leicestershire LE11 3TU，UK

dState Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China

Scour depth beneath a pipeline undergoing forced vibration

Y.Luana，D.Liangb，∗，R.Ranac，d

aDepartment of Engineering，University of Cambridge，Cambridge CB2 1PZ，UK

bMOE Key Laboratory of Hydrodynamics，Shanghai Jiao Tong University，Shanghai 200240，China

cSchool of Business and Economics，Loughborough University，Leicestershire LE11 3TU，UK

dState Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China

A R T I C L E I N F O

Article history:

Received 23 October 2014

Accepted 9 January 2015

Available online 7 March 2015

Offshore pipelines

Scour

Numerical models

Vibration

Sediment transport

This paper studies the coupling effect of the pipeline vibration on the seabed scour.A vertical twodimensional model is applied to numerically investigate the local scour below a vibrating pipeline with different amplitudes and periods.Using the scour underneath a fixed pipeline as a reference，this paper focuses on the impact of the pipeline vibration on the equilibrium scour depth.Generic relationships are established between the non-dimensional scour depth and the non-dimensional vibrating parameters，i.e.，amplitude and frequency.The normalization process takes into account the influences of such parameters as the incoming flow velocity，pipe diameter，and Shields parameter.An empirical formula is proposed to quantify these relationships.

©2015 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY license（http://creativecommons.org/ licenses/by/4.0/）.

When an offshore pipeline is laid on the seabed，the original flow field is disturbed；if the seabed is erodible，the large pressure difference between the upstream and the downstream sides of the pipe induces the seepage flow in the sand beneath the pipe. Once the seepage-induced pressure gradient exceeds a certain threshold，piping occurs and some sand particles are carried away，forming a small tunnel underneath the pipeline.As water rushes through the gap between the pipe and the seabed，the scour hole enlarges and eventually reaches an equilibrium state.The formation of the scour hole poses a great threat to the integrity of the structure，which may lead to either instant failure or fatigue failure of the pipeline.According to the pipe failure statistics［1］，44.3%of the accidents happened in Mississippi Delta and the Gulf of Mexico were caused by the free-span development.

Around a fixed pipe，the enlargement of the scour hole has been extensively studied，in both current［2，3］and wave［3，4］conditions.There have also been some studies on the scour processes around flexible pipelines undergoing vortex-induced vibrations. The vibration becomes pronounced when the vortex shedding frequency is close to the excitation frequency of the structure.In the tests conducted by Tsahalis［5］，the pipeline was placed near a rigid boundary and allowed to move in two directions to determine the vortex-induced vibration of the flexibly-mounted pipelines.The results show that the transverse vibration amplitude was much larger than the in-line amplitude.Hence，it is reasonable to simplify the problem by confining the pipe vibration in the transverse direction only.Sumer etal.［6］analyzed the influence ofpipe vibration on the scour depth and width.Both the depth and the width of scour beneath a vibrating pipe were shown to be larger than those of a fixed pipe.In recent years，more experimental studies have been carried out to gain better understanding of the relationship between the vortex-induced vibration and the bed scour［7，8］.There have also been reports on the two-degree-of-freedom vortex-induced vibration of offshore pipelines and their influence on the scour underneath［9，10］.However，few reports can be found on the scour around flexible pipes undergoing forced vibrations. The objective ofthis study is to establish the relationships between the vibrating amplitude，frequency，and the scour depth when the pipeline is experiencing forced vibration.To the knowledge of the author，this relationship has never been studied in a systematic manner so far.

The numerical model used in this study was developed by Liang et al.［11，12］，which has since been extensively validated［13］.The model consists of three parts:a flow model，a sediment transport model，and a bed morphological model.The unsteady Reynoldsaveraged Navier-Stokes equations govern the fluid flow around the pipeline，together with the low-Reynolds-number k-ωturbulence model.The sediment transport includes two separate parts: the bed load，which is assumed to be confined within a bed layer with a thickness of two times the grain diameter，and the overlying suspended load.The well-known Meyer-Peter and Müller formula is used to estimate the bed load，whereas the suspended load is quantified by solving the advection-diffusion equation for the suspended sediment concentration.The evolution of the bed is calculated based on the mass conservation of the sediment material in control volumes extending from the immobile bed to the water surface.

These partial differential equations，including the Reynoldsaveraged Navier-Stokes equations，the transport equations for the turbulent kinetic energy and the turbulent specific dissipation rate，the advection-diffusion equation for the suspended sediment concentration，and the bed deformation equation（the so-called Exner’s equation），are solved with a second-order finite difference method formulated in a boundary-fitted curvilinear coordinate system.The curvilinear mesh in the physical domain is mapped onto the uniform rectangular mesh in the computational domain. Correspondingly，the governing equations are also transformed into the computational domain.The mesh in the computational domain remains unchanged during the whole simulation，whereas the mesh in the physical domain keeps changing during the scour.Extra terms in the transformed equations have been added to handle the moving solid boundaries.The pressure Poisson equation method is employed to couple the velocity and pressure in solving the Navier-Stokes equations.An efficient time marching algorithm is used to speed up the computation［11］.

A panoramic view of the computational domain is shown in Fig.1，where D is the pipe diameter.The inlet and outlet are placed at 20D upstream and 30D downstream of the pipe，respectively. The water depth is 4D，in accordance with the water depth adopted in the experiments［6］.The pipe is initially placed in contact with the sand bed.To facilitate the scour simulation，a small opening is introduced beneath the pipe.

The model is first validated against the experiments conducted by Sumer et al.［6］，with a pipe diameter of 100 mm and a median grain size of the sediment of 0.36 mm.The depth-average flow velocities U in the two separate runs are 350 mm/s and 500 mm/s， corresponding to the undisturbed Shields parameters of 0.048 and 0.098，respectively.The development of the scour depth and the scour profile are the two main considerations.Comparison of the scour depth developmentbetween the measured and predicted results in the fixed-pipe condition is shown in Fig.2（a）.The equilibrium scour depth at a larger Shields parameter is deeper by about 30%，and the scour also develops much faster.When the pipe is allowed to vibrate in the vertical direction，the experiments［6］show that the vortex-induced vibration is hardly noticeable until the gap between the pipe and the seabed is sufficiently large. From then on，the amplitude and frequency of the vibration remain almost constant.With the incoming velocities of 500 mm/s and 350 mm/s，the observed vibration amplitudes at the equilibrium stage are 0.64D and 0.62D，respectively，and the dominant frequencies are 729.7 mHz and 826.3 mHz，respectively.

In the vibrating-pipe case，the main numerical difficulty is the possible collision between the pipe and the seabed.The collision distorts the topology of the computational mesh，and leads to the collapse of the simulation.An approximation method is adopted herein to cope with this problem.The simulation of the scour under a vibrating pipe is divided into two periods:fixed-pipe period and vibrating-pipe period.The pipe is initially fixed until the scour depth reaches a significant value，from which point the vibration starts at the aforesaid constant amplitude and frequency. According to the experiments，the vibrating-pipe period starts 200 min after the onset of scour at 500 mm/s and 15 min after the onset of scour at 350 mm/s.This treatment not only avoids the collision issue when the vibration takes place over a relatively shallow scour hole，but also largely reflects the experimental observation and standardizes the simulation.

Fig.2.Scour depth development:（a）fixed pipes，（b）vibrating pipe at 350 mm/s，（c）vibrating pipe at 500 mm/s.

The measured and computed time developments of the scour depth S underneath the pipe center are plotted in Figs.2（b）and 2（c）.A distinct inflection point is observed in the curve with the incoming flow velocity of 350 mm/s，which is due to thecommencement of the pipe vibration at 200 min into the scour. The vibration causes a steep rise in the scouring rate.However，this feature is not very clear in Fig.2（c），which is due to the earlier commencement of the vibration at higher flow velocity.When the vibration is introduced at 15 min after the onset of scour，the scour depth has already been around 0.7D and it is stillincreasing rapidly at this stage.Although the pipe vibration enhances the scour，it is not enough to produce an apparent change of scouring rate.

The predicted and measured equilibrium scour profiles at two flow velocities are compared in Fig.3.Each figure includes the fixed-pipe and vibrating-pipe results.Although the numerical model tends to slightly overestimate the scour depth directly underneath the pipeline，the predicted shape of the scour resembles the measured profiles well in all cases，particularly the upstream part of the scour hole.When the pipe vibrates，both the width and depth of the scour are clearly enhanced.

Fig.3.Comparison of scour profiles at equilibrium stage.（a）U=350 mm/s，（b）U=500 mm/s.

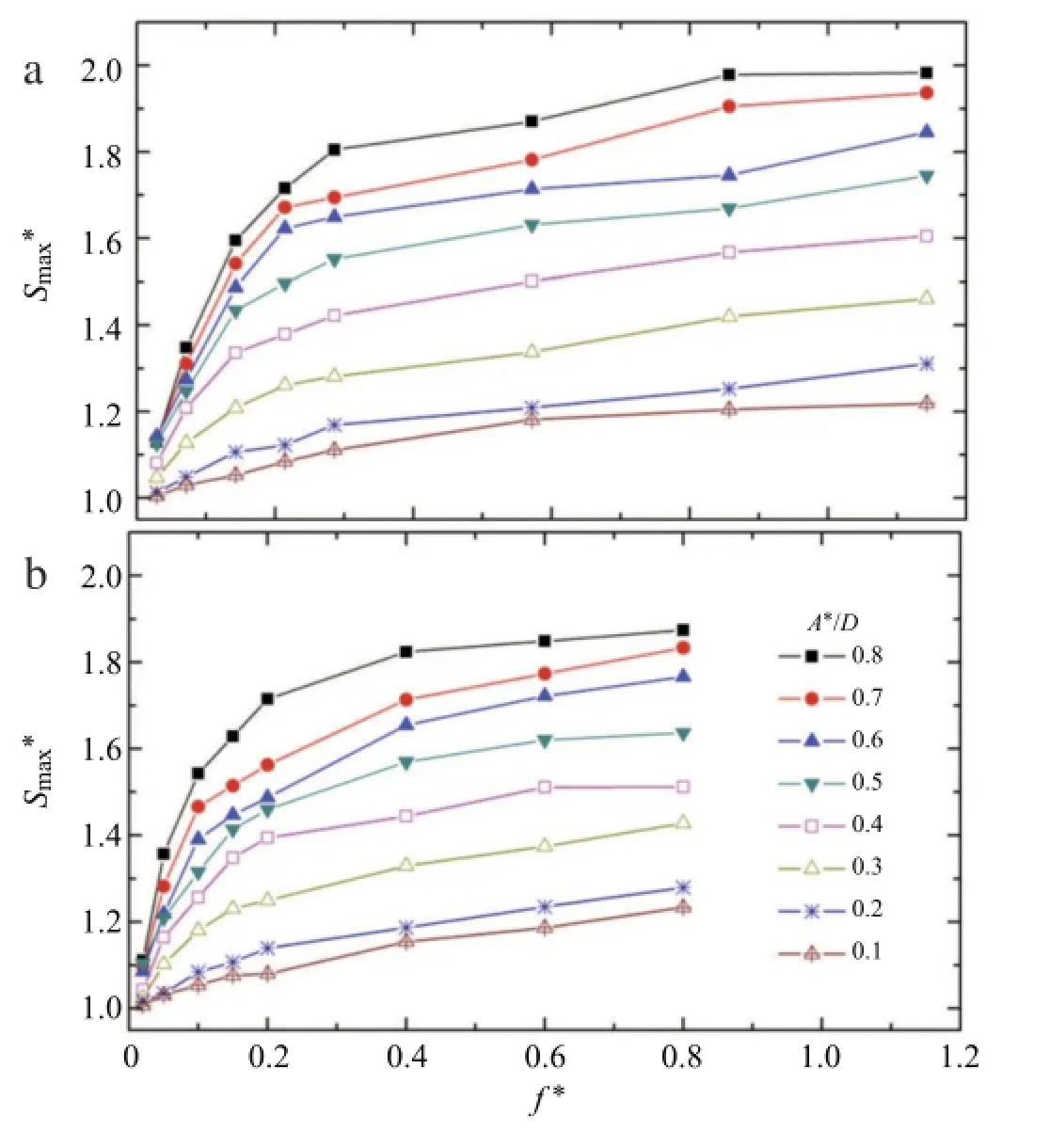
Fig.4.Scour depth variation with frequency and amplitude.（a）U=350 mm/s，（b）U=500 mm/s.

A constant of 1.0 is introduced on the right hand side，because the equilibriumscour depth should return to the value ofthe fixed pipe at zero amplitude.From Eq.（1），the sensitivity of the parametersA∗and f∗can be deduced.Both their exponents are smaller than 1，suggesting that the increase rate of the scour depth decreases with the increase of A∗and f∗.The exponent of A∗is larger than that of f∗，signifying that the influence of f∗is more significant when it is relatively small.As f∗gets larger，its importance diminishes，and A∗exerts a bigger influence on the scour.It is expected that this empirical equation can be extended to other situations when all the variables are normalized in the fashion proposed in this paper.

Fig.5.Three-dimensional depiction of the fitted formula.

Fig.6.Two-dimensional depiction of the fitted formula.

The fitted surface defined by Eq.（1）is presented in Fig.5，with the calculated results displayed as the scattered points.It can be seen that Eq.（1）fits the calculated results well，especially at higher frequencies.When frequencies are small and amplitudes are large，Eq.（1）slightly underestimates the scour depth.The fitted relationship is overlapped with the calculated data at typical vibration amplitudes in Fig.6，which further confirms the appropriateness of the proposed equation.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（51479111）and the Open Fund at the State Key Laboratory of Hydraulics and Mountain River Engineering，China（SKHL1404）.

［1］J.B.Herbich，Offshore Pipeline Design Elements，Marcel Dekker Inc.，New York，1981.

［2］Y.M.Chiew，Prediction of maximum scour depth at submarine pipelines，J.Hydraul.Eng.117（1991）452-466.

［3］E.W.Bijker，W.Leeuwestein，Interaction between pipelines and the seabed under the influence of waves and currents，in:Seabed Mechanics，Springer，Netherlands，1985，pp.235-242.

［4］B.M.Sumer，J.Fredsøe，Scour below pipelines in waves，J.Waterw.Port Coastal Ocean Eng.116（1990）307-323.

［5］D.T.Tsahalis，Vortex-induced vibrations of a flexible cylinder near a plane boundary exposed to steady and wave-induced currents，J.Energy Resour. Technol.106（1984）206-213.

［6］B.M.Sumer，Y.Mao，J.Fredsøe，Interaction between vibrating pipe and erodible bed，J.Waterw.Port Coastal Ocean Eng.114（1988）81-92.

［7］B.Yang，F.P.Gao，D.S.Jeng，Y.X.Wu，Experimental study of vortex-induced vibrations of a pipeline near an erodible sandy seabed，Ocean Eng.35（2008）301-309.

［8］F.P.Gao，B.Yang，Y.X.Wu，S.M.Yan，Steady current induced seabed scour around a vibrating pipeline，Appl.Ocean Res.28（2006）291-298.

［9］M.Zhao，L.Cheng，Numerical investigation of local scour below a vibrating pipeline under steady currents，Coast.Eng.57（2010）397-406.

［10］M.Zhao，L.Cheng，Numerical simulation of two-degree-of-freedom vortexinduced vibration of a circular cylinder close to a plane boundary，J.Fluids Struct.27（2011）1097-1110.

［11］D.Liang，L.Cheng，F.Li，Numericalmodeling offlow and scourbelow a pipeline in currents，part II:scour simulation，Coastal Eng.52（2005）43-62.

［12］D.Liang，L.Cheng，K.Yeow，Numerical study of the Reynolds-number dependence of two-dimensional scour beneath offshore pipelines in steady currents，Ocean Eng.32（2005）1590-1607.

［13］D.Liang，L.Cheng，Numerical study of scour around a pipeline bundle，Proc. ICE-Marit.Eng.161（2008）89-95.

∗Corresponding author.

E-mail address:dl359@cam.ac.uk（D.Liang）.

*This article belongs to the Solid Mechanics