利用行列式的几何意义解释Cramer法则

王娇

（长治学院 数学系，山西 长治 046011）

利用行列式的几何意义解释Cramer法则

王娇

（长治学院 数学系，山西 长治 046011）

文章引入了体积函数的概念，给出了三阶行列式的几何意义，并利用该几何意义解释三元线性方程组的Cramer法则。

体积函数；行列式；Cramer法则

1 引言

首先给出体积函数的定义如下：

定义1设A=（α1，α2，α3）∊R3×3，V（A）表示以α1,α2,α3为邻边的平行六面体的体积，称V（A）为关于矩阵A的体积函数。

显然，若α1，α2，α3线性相关，记V（A）=0，而det（A）=0，有det（A）=V（A）。若α1，α2，α3线性无关，特别地，当A为单位矩阵时，V（A）表示以

为邻边的正方体（如图1）的体积，即V（A）=1，而det（A）=1，有det（A）=V（A）。

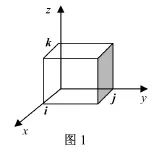
但det（A）可正可负，而V（A）≥0，故考虑在一般情况下，对于∀A∊R3×3，是否都有V（A）＝det（A）的问题。

2 行列式的几何意义

2.1 体积函数的性质

下面三阶行列式的列的性质可以推广到体积函数中来。

（1）交换行列式两列，行列式改变符号；

（2）把行列式某一列的倍数加到另一列，行列式的值不变；

（3）用一个数乘行列式某一列的所有元素就等于用这个数乘此行列式。

对A=（α1，α2，α3）∊R3×3，则相应的体积函数的性质如下：

（1）交换A的任意两列，V（A）保持不变；

2.2 行列式的几何意义

在一般情况下，设

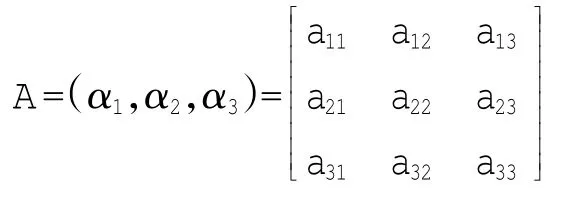
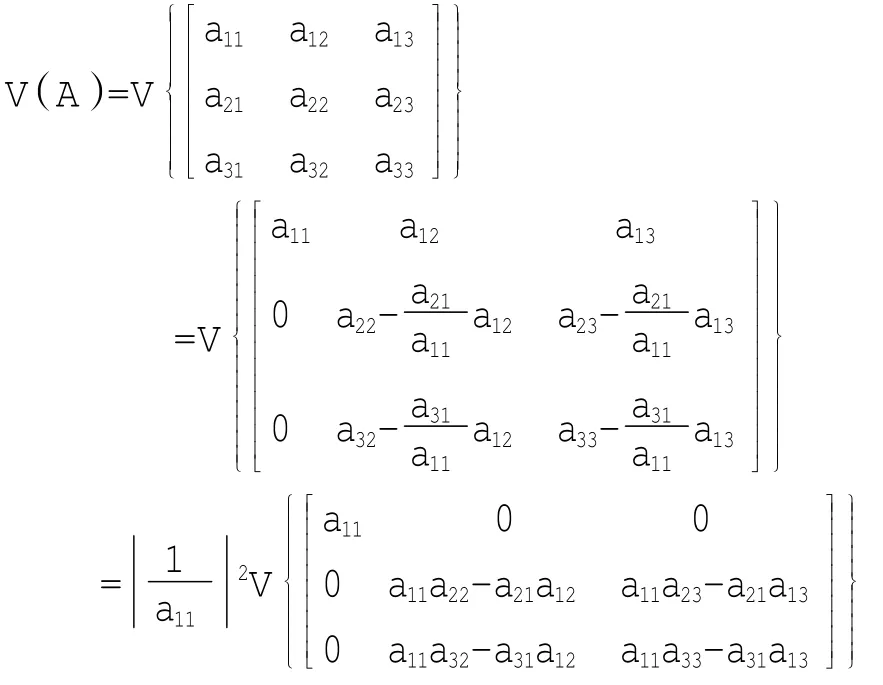
3 Cramer法则的几何解释

设有三元线性方程组

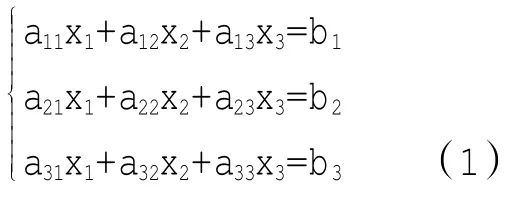
将它写成向量的形式：

为了几何解释的方便起见，设x1，x2，x3＞0。考虑分别由向量x1α1，x2α2，x3α3和向量b，x2α2，x3α3生成的两个平行六面体（如图2）

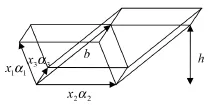
这两个平行六面体有相同的由x2α2，x3α3生成的底面，它们也有相同的高h（这是因为由(2)式可知，它们的顶面含于同一个平面内），所以它们有相同的体积，即

由行列式的几何意义可知

从而可得

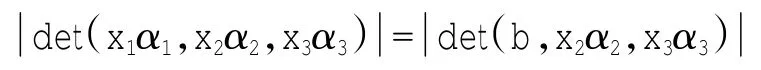
实际上，由(2)式可知

从而有

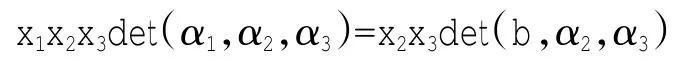
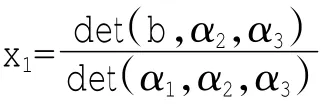
同样可以求出x2，x3。这样，利用体积函数解释了三元线性方程组的Cramer法则。

［1］北京大学数学系前代数小组.高等代数（第四版）［M］.北京：高等教育出版社，2013.

［2］邱森，朱林生.高等代数探究性课题精编［M］.武汉大学出版社，2012.

［3］赵振华.广义行列式与Cramer法则［J］.数学通

报，1993(9)：41-43.

［4］陈永林.约束线性方程组通解的显式表示及Cramer法则［J］.高校应用数学学报，1993，8(1)：61-70.

［5］王娇，张凯院，李书连.多矩阵变量线性矩阵方程的广义自反解的迭代算法［J］.数值计算与计算机应用，2013,34(1):9-19.

（责任编辑 赵巨涛）

0151.22

A

1673-2015（2015）05-0038-02

2015—06—17

王娇（1988—）女，山东济南人，硕士研究生，主要从事计算数学研究。