如何判断相对面

如何判断相对面

□赵国瑞

在学习《几何图形初步》一章时，我们会遇到一类判断正方体或其表面展开图的相对面的问题.对于这类问题，很多同学不知从何下手，其实只要能抓住正方体或其表面展开图的一些基本特征，解答此类问题并不困难.

一、已知一个正方体的三种不同的摆法或从三个不同角度观察到的图形判断相对面

图1

如图1，一个正方体的6个面上分别标有字母A、B、C、a、b、c，其中A的对面是a，B的对面是b，C的对面是c.观察图1可知，与A相邻的4个面是：B、b、C、c，与B相邻的4个面是：A、a、C、c，与a相邻的4个面是：B、b、C、c.

思考1：与A、a相邻的4个面都是B、b、C、c，而A、a是一对相对面据此你有什么发现？

结论1：与某4个面都相邻的两个面是一对相对面.

思考2：与A相邻的4个面是B、b、C、c，与B相邻的4个面是：A a、C、c，因此与A、B都相邻的面是C c，而C、c是一对相对面，据此你又有什么发现？

结论2：与两个相邻面都相邻的两个面是一对相对面.

由此我们可以得到判断正方体相对面的两种方法.

例1有一个正方体，6个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示.如果记6的对面的数字为a，的对面的数字为b，那么a＋b的值为（）

图2

A.3B.7

C.8D.11

解析：由图2①和图2②知与1相邻的面是2、3、4、6，可知面5必然是面1的相对面.

由图2②和图2③知，与3相邻的面是1、2、4、5，可知面6必然是面3的相对面.

剩下的2与4当然是相对面了.于是a＝3，b＝4，a＋b＝7.选B.

例2一个立方体木块的6个面分别标有1、2、3、4、5、6.图3是从不同的方向观察这个立方体木块看到的数字情况，数字1、数字5对面的数字和是________.

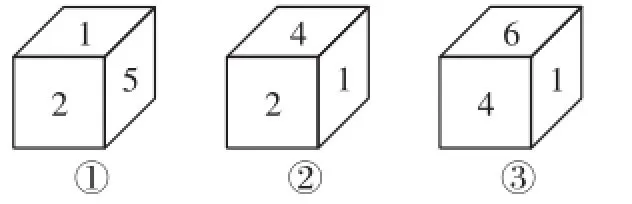
图3

解析：由图3①和图3②可知与1、2都相邻的面是4、5，由结论2可知4与5是一对相对面.由图3②和图3③可知与1、4都相邻的面是2、6，由结论2可知2与6是一对相对面.剩下的1与3是相对面.于是数字1、数字5对面的数字和是7.

二、已知一个正方体的表面展开图判断相对面

正方体的表面展开图一共有11种：

1.“1-4-1”型.如图4（1）-（6），有4个面处在同一行，其余两个面分别位于这一行的两侧.

2.“2-3-1”型.如图4（7）-（9），有3个面在一行，其余3个面分别位于两侧.

3.“2-2-2”型.如图4（10），每行有两个面，形成“阶梯形”.

4.“3-3”型.如图4（11），共有两行，每行3个面，且两行之间只有一个面有公共边.

图4

观察图4我们发现，正方体的相对面有两种类型：一类是位于同一行（或同一列），中间间隔一个面的两个面是相对面.如图4（1）中的2个b位于同一行，中间间隔一个面c，它们是相对面，2个c也位于同一行，中间间隔一个面b，它们是相对面.再如图4（7）中有2个b位于同一列，中间间隔一个面c，它们是相对面.

另一类是位于同一行（或同一列）的两侧，且与该行（或列）中的某一面有一条公共边的两个面是相对面.如图4（5）中第1行的a与第2行中的c有一条公共边，第3行的a与第2行中的b有一条公共边，它们是相对面.再如图4（10）中第2列的c与第3列的a有一条公共边，第4列的c与第3列的b有一条公共边，它们是相对面.

说明：本文中的第几行是指从上至下数第几行，第几列是指从左至右数第几列.

由此我们得到判断正方体表面展开图相对面的两种方法：

结论3：位于同一行（或同一列），中间间隔一个面的两个面是相对面.

结论4：位于同一行（或同一列）的两侧，且与该行（或列）中的某一面有一条公共边的两个面是相对面.

图5

例3如图5是正方体的展开图，则原正方体相对两个面上的数字和最小的是（）.

A.4B.6

C.7D.8

解析：2与6位于同一列，它们之间相隔一个面5，由结论3知，面与面6是相对面.面3与面4位于第2列的两侧，且面3与第2列中的面5有一条公共边，面4与第2列中的面2有一条公共边，由结论4知，面与面4是相对面.剩下的面1与面是相对面.

由于相对面上的数字和分别为2＋6＝8，3＋4＝7，1＋5＝6，因此最小的是6，答案选B.