充分利用元素法进行二重积分计算的教学
赵翠新
(赤峰学院 数学与统计学院,内蒙古 赤峰 024000)
元素法是解决某些问题常用的方法,学习一元函数的定积分时我们就用元素法求过平面区域的面积、旋转体的体积、平面曲线的弧长、变力做功、水压力等问题.主要分这样几个环节:首先对要求的整体问题进行分解,接着对分解后的每个元素求出近似值,然后把各个近似值进行求和,最后对近似值的和取极限得到整体问题的精确值.这其中最关键的一步是怎样分解,因为分解方式会决定下一步近似值的求解方式和难易程度.而如何分解又需要我们根据问题实际情况选择恰当的方式进行,保障问题得到顺利解决.
二重积分的定义和计算其实都是利用元素法给出的,只是没有明确提出.尤其二重积分的计算一般直接介绍根据平面区域的形状划分成直角坐标下的X型或Y型,或是用极坐标计算,而这些恰好是学生容易有疑惑的地方.所以本文将以曲顶柱体的体积为例,充分利用元素法,通过不同的分解方式,加深对二重积分定义的理解,并进一步说明二重积分几种常用的计算方法是怎样得出的.
1 结合元素法加深对二重积分定义的理解
设曲顶柱体的底是xoy面上的有界区域D,顶是连续曲面z=f(x,y).要求的问题是曲顶柱体的体积V.
首先我们按照元素法进行第一步:分解.用垂直于xoy面的两组柱面将原来的曲顶柱体分成n个细曲顶柱体.如图1,每个小柱体底的面积记为△σ1,△σ2,…,△σn;
接着对每个元素求近似值:由于f(x,y)连续,每个细曲顶柱体的高变化不大.将顶看作平的,于是得到每个元素细曲顶柱体的近似值f(ξi,ηi)△σi.
然后求和得整个柱体的近似值
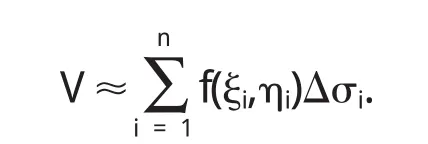
最后取极限让 λ={maxσi,i=1,2,…n},得
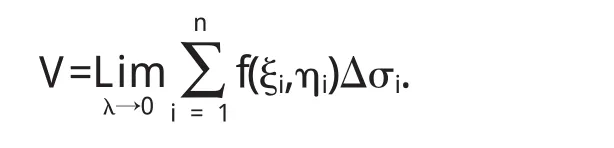
这个过程恰好利用了元素法,此类问题定义为二重积分
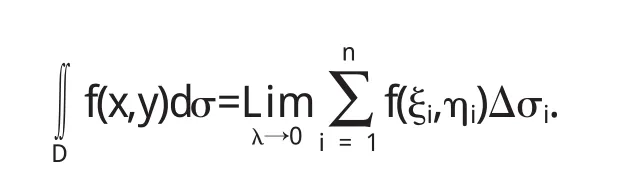
若用平行于zox坐标面和yoz坐标面的两组平面来划分,那么除边界的一些之外,多数细曲顶柱体的底都是矩形,因此二重积分也可表示成为dxdy.也就不难理解了.
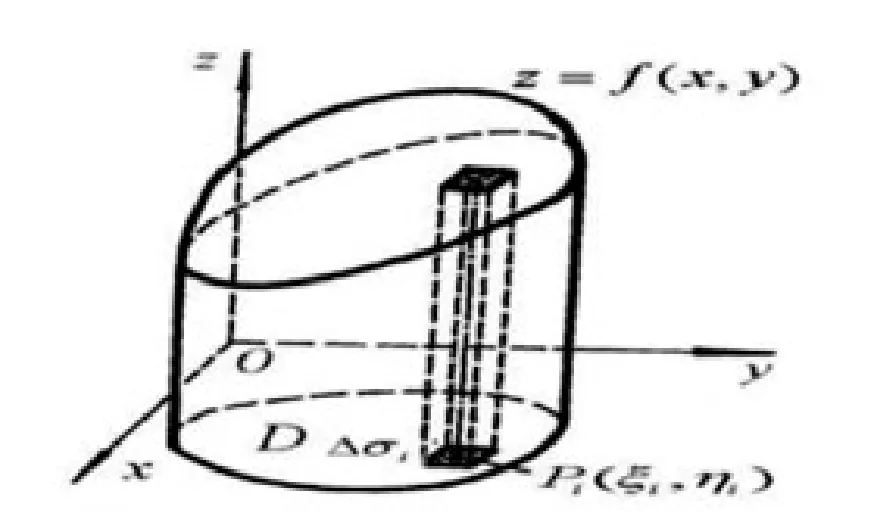
图1
2 利用元素法根据不同的分解方式得到不同的计算过程
利用曲顶柱体的体积定义的二重积分虽然用了元素法,但这个过程却不适合对二重积分进行计算. 因为每个细曲顶柱体的底形状面积和高都不尽相同,也不能用统一的表达式表示,所以按此方式划分只能定义不能计算.也因此我们改用其它划分方式使计算可行且简单.
若区域 D是由 c≤y≤d,x1(y)≤x≤x2(y)所围成的,则我们可以选择下面的分解方式利用元素法来计算二重积分的值.首先用平行于zox坐标面的一组平面划分曲顶柱体成很多平行于zox坐标面的薄片,其中第i片厚度记为△yi,截面是从x1(yi)到x2(yi)为底,z=f(x,yi)为曲边的曲边梯形;然后求薄片的体积近似值,由于薄片很薄,左右截面面积近似相等即,所以薄片体积为A(yi)△yi=接着我们把所有薄片的体积累加起来,求和得近似值;最后取 △yi趋于零时的极限得即
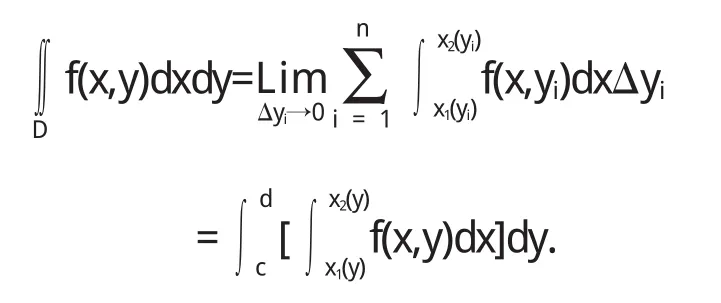
至此在这样的区域 c≤y≤d,x1(y)≤x≤x2(y)上二重积分计算问题得到了解决,即化成了二次积分.这说明利用元素法按照这样的切片的分解方式能够计算二重积分,简单可行.
如 D是 0≤y≤1,y2≤x≤2-y,则
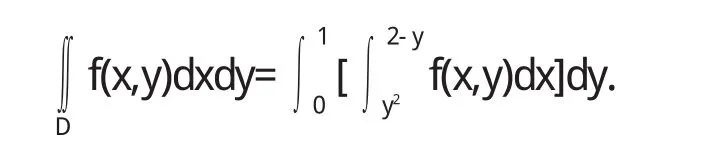
若改用其它的分解方式,比如用平行于yoz坐标面的一组平面去切分,则分解后的薄片也是以大小不等的曲边梯形为截面的,但此时的曲边梯形的底就是长短不一变化多端的.截面的面积也就不能用一个通式来表示,曲顶柱体的体积也就没法再求下去了,所以选择什么样的分解方式非常关键.一般我们把变化范围是常数的变量后积分,也就是用垂直于变化范围是常数的这个轴的一组平面去切.
若区域 D是由 a≤x≤d,y1(x)≤y≤y2(x)所围成的,就用平行于yoz坐标面的一组平面划分,同样利用元素法可得
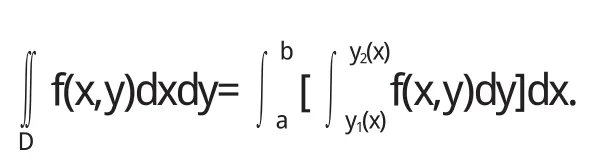
如 D是由 0≤x≤1,x3≤y≤x2,则
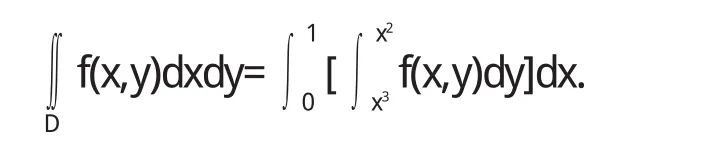
若区域是在极坐标下或是其它类型的,也都需要利用元素法构造或计算二重积分,根据区域形状及被积函数类型选择恰当的分解方式决定恰当积分次序,问题就迎刃而解了.
〔1〕欧阳光中,朱学炎等.数学分析[M].北京:高等教育出版社,2007.
〔2〕刘玉琏,傅沛仁,等.数学分析讲义[M].北京:高等教育出版社,2005.

