三角代数上的广义Jordan左导子

三角代数上的广义Jordan左导子

刘莉君

(陕西理工学院 数学与计算科学学院， 陕西 汉中 723000)

[摘要]运用算子论的方法研究三角代数上的广义Jordan左导子，证明了三角代数上的广义Jordan左导子是广义左导子，给出三角代数上广义左导子的一种表示定理及关于广义Jordan左导子的相关性质。

[关键词]三角代数；广义Jordan左导子；广义左导子

[文章编号]1673-2944(2015)04-0068-03

[中图分类号]O177.1

收稿日期：2015-01-06

基金项目：陕西省教育厅自然科学研究计划项目(2013Jk0571)

作者简介：刘莉君(1980—)，女，陕西省城固县人，陕西理工学院讲师，硕士，主要研究方向为算子代数和算子理论。

设Γ是可交换环R上的一个代数，Z(Γ)为其中心。如果σ(xy)=σ(x)y+xσ(y)(∀x,y∈Γ)，称线性映射σ:Γ→Γ是一个导子；如果σ满足σ(x2)=σ(x)x+xσ(x)(∀x,y∈Γ)，则称它是一个Jordan导子；如果δ(xy)=xδ(y)+yδ(x)(∀x,y∈A)，称线性映射δ:Γ→Γ是一个左导子；如果δ满足δ(x2)=2xδ(x)(∀x∈Γ)，则称它是一个Jordan左导子；如果φ满足φ(xy)=xφ(y)+δ(x)y，其中δ是从Γ到自身上的Jordan左导子，则称φ是一个广义左导子；如果满足φ(x2)=xφ(x)+xδ(x)，则称φ是一个广义Jordan左导子；显然，每个广义左导子都是广义Jordan左导子，但反之并一定成立。本文受文献[1-7]的启发，讨论了三角代数上的广义Jordan左导子，得出结论三角代数上的广义Jordan左导子都是广义左导子，从而推广了三角代数上的Jordan左导子的主要结果。

本文设A,B是交换环R上的具有单位元的代数，M既是左A-模又是右B-模(此时，称M是(A,B)-双边模)。如果

则称M是(A,B)-忠实双边模。

记

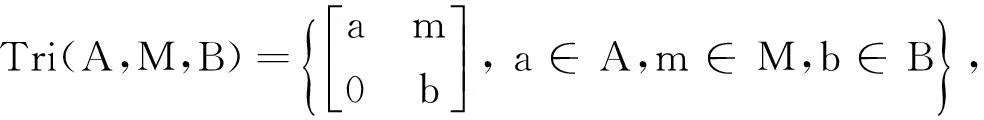
容易看出，满足矩阵加法、数乘与乘法运算，故Tri(A,M,B)为一个代数，称为三角代数[8]。

定理1设U=Tri(A,M,B)为三角代数，映射φ是从U到自身上的广义Jordan左导子，映射δ是从U到自身上的Jordan左导子，则对于任意的x,y,z∈U，有

(Ⅰ)φ(xy+yx)=xφ(y)+yφ(x)+xδ(y)+yδ(x)；

(Ⅱ)φ(xyx)=xyφ(x)+2xyδ(x)+x2δ(y)-yxδ(x)；

(Ⅲ)φ(xyz+zyx)=xyφ(z)+zyφ(x)+2xyδ(z)+2zyδ(x)+xzδ(y)+zxδ(y)-yxδ(z)-yzδ(x)。

证明(Ⅰ)因为映射φ是U上的一个广义Jordan左导子，因此就有φ(x2)=xφ(x)+xδ(x)，则

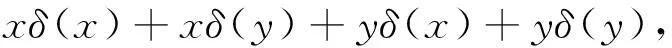
(1)

另一方面，

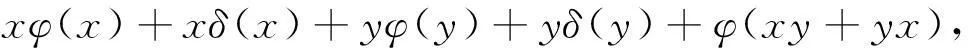
(2)

由(1)和(2)式可得

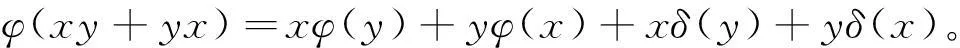
(Ⅱ)在等式φ(xy+yx)=xφ(y)+yφ(x)+xδ(y)+yδ(x)中用xy+yx替代y可得

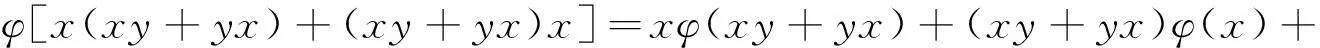
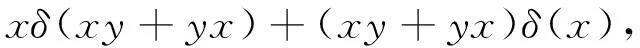
(3)

又因为映射δ是三角代数U到它自身上的Jordan左导子，故

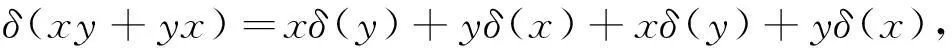
(4)

综合(3)和(4)式可得

(5)

另一方面

(6)

由(5)和(6)式可得

(Ⅲ)在(Ⅱ)的等式中用x+z替代x可得

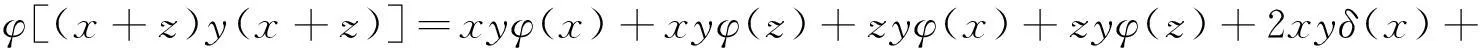
(7)

另一方面

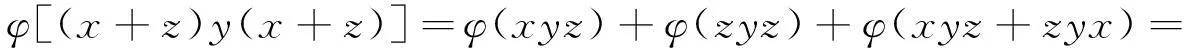
(8)

由(7)和(8)式可得

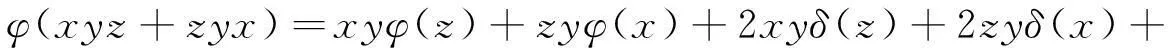
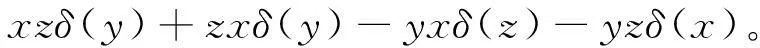
证毕。

引理1[9]设U=Tri(A,M,B)为三角代数，如果映射δ是从U到它自身上的Jordan导子，则U上的每一个Jordan导子都是导子，即对于任意的x,y∈U，有

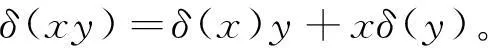
引理2设U=Tri(A,M,B)为三角代数，φ是从U到它自身上的一个线性可加映射，对于任意的x,y∈U，则有

(Ⅰ)若φ(x2)=φ(x)x，则φ(xy)=φ(x)y；

(Ⅱ)若φ(x2)=xφ(x)，则φ(xy)=xφ(y)。

证明(Ⅰ)因为φ是从U到它自身上的一个线性可加映射且满足φ(x2)=φ(x)x，故

(9)

在(9)式中用xy+yx替代y可得

(10)

又因为

(11)

由(10)和(11)式可得

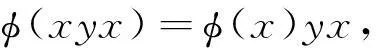
(12)

再在(12)式中用x+z替代x可得

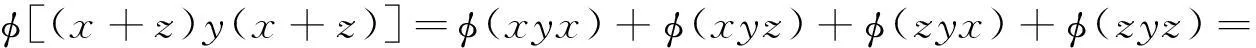
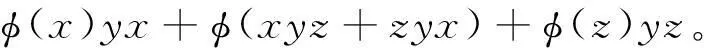
(13)

另一方面

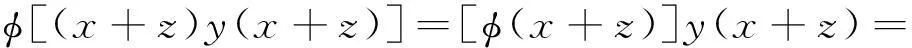
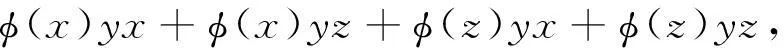
(14)

由(13)和(14)式可得

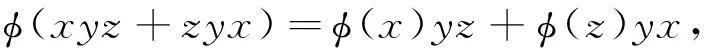
(15)

由(12)式可得

φ(xyzyx+yxzxy)= φ[x(yzy)x+y(xzx)y]=

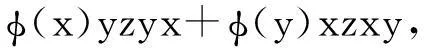
(16)

由(15)式可得

φ(xyzyx+yxzxy)= φ[(xy)z(yx)+(yx)z(xy)]=

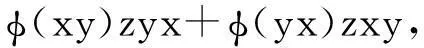
(17)

综合(16)和(17)式就有

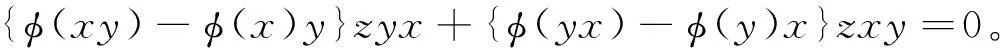
(18)

不妨设B(x,y)=φ(xy)-φ(x)y，则(18)式可写成B(x,y)zyx+B(y,x)zxy=0(∀x,y∈U)。又结合(9)式易证得B(x,y)=-B(y,x)，即有B(x,y)z(yx-xy)=0，又因为任意的x,y,z∈U，故z(yx-xy)≠0，则B(x,y)=0，即φ(xy)=φ(x)y。证毕。

类似于结论(Ⅰ)，同理可证结论(Ⅱ)：若φ(x2)=xφ(x)，则φ(xy)=xφ(y)成立。

定理2设U=Tri(A,M,B)为三角代数，如果线性可加映射φ是U上的一个广义Jordan左导子，则线性可加映射φ也是三角代数U上的一个广义左导子，即满足φ(xy)=xφ(y)+yδ(x)。

证明对于该定理分两种情况证明。

(1)若δ=0时，因为线性可加映射φ是U上的一个广义Jordan左导子，即有φ(x2)=xφ(x)，故由引理2中(Ⅱ)可得φ(xy)=xφ(y)。因此线性可加映射φ是三角代数U上的一个广义左导子。

(2)若δ≠0时，因为φ,δ,φ都是U上的线性可加映射，故不妨设φ=φ-δ，因此就有

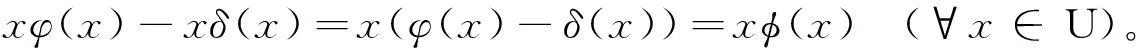
由引理2中(Ⅱ)可得φ(xy)=xφ(y)，即(φ-δ)(xy)=x[(φ-δ)(y)]，展开可得φ(xy)-δ(xy)=xφ(y)-xδ(y)，又由引理1可知δ(xy)=δ(x)y+xδ(y)，故

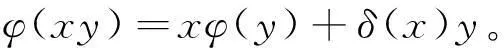
综上可知，三角代数上的每一个广义Jordan左导子都是三角代数上的广义左导子。证毕。

注由定理可知，三角代数上的广义Jordan左导子和广义左导子互相等价。

[参考文献]

[1]EBADIAN A.Left Jordan derivations on Banach algebras[J].Iran J Math Sci Inform,2011,6(1):1-6.

[2]LI Jian-kui,ZHOU Ji-ren.Jordan left derivations and some left derivable maps[J].Oper Matrices,2010,4(1):127-138.

[3]余维燕,邢福弟.三角代数上的广义Jordan导子[J].数学进展,2009,25(4):72-78.

[4]刘莉君.Banach代数上的高阶Jordan-triple导子系的广义Hyers-Ulam-Rassias稳定性[J].纯粹数学与应用数学,2011,27(5):643-649.

[5]刘莉君.关于三角代数上的导子系[J].陕西理工学院学报:自然科学版,2011,27(2):66-69.

[6]REHMAN N.On lie ideals and generalized Jordan left derivations of prime rings[J].Ukrainian Mathematics Journal,2014,65(8):1118-1125.

[7]JUNG Y S,PARK K H.Left Jordan derivations on Banach algebras and related mappings[J].Bull Korean Math Soc,2010,47(1):151-157.

[8]CHEUNG W S.Commuting maps of triangular algebras[J].Journal of the London Mathematical Society,2011,63(1):117-127.

[9]ZHANG Jian-hua,YU Wei-yan.Jordan derivations of triangular algebras[J].Linear Algebra and its Applications,2006,419(1):251-255.

[责任编辑：魏 强]

Generalized Jordan left derivation of triangular algebra

LIU Li-jun

(School of Mathematics and Computer Science, Shaanxi University of Teachnology,

Hanzhong 723000, China)

Abstract:By using operator theory methods to study generalized Jordan left derivation in triangular algebra, it is proved in the study that every generalized Jordan left derivation on a triangle algebra is a generalized left derivation on a triangle algebra. The study derives a representation theorem for the generalized left derivation and relevant property about generalized Jordan left derivation.

Key words:triangular algebra;generalized Jordan left derivation;generalized left derivation