关于带参数多项式曲线的讨论
邢庆丹,陈雪娇,潘晶
(辽宁师范大学数学学院,大连 116029)
关于带参数多项式曲线的讨论
邢庆丹,陈雪娇,潘晶
(辽宁师范大学数学学院,大连 116029)
通过对带参数的多项式基函数构造原理的分析,得到新的基函数构造方法。利用此法构造控制点可调整的三次带参数的多项式曲线,同时给出曲线在拼接点处达到一定连续性的条件。
参数;多项式曲线;基函数;连续性
0 引言
为了调整Bézier曲线和均匀B样条曲线的形状,在它们的生成基中引入了参数。文献[4]、[7]中的基函数是在二次Bernstein基函数中融入带两个或多个形状参数的函数,将二次Bernstein基函数扩展为高次基函数;文献[6]给出一种n次Bernstein基函数的扩展;文献[2]是先构造带形状参数的三阶B样条基函数,再利用积分方法推广至高阶;文献[5]是在最优规范全正基的基础上乘以全正的转化矩阵,得到新的含参数的规范全正基。基于n次Bernstein基与幂基的关系,本文研究发现这类带参数的基函数[2-8]均可转换成Bernstein基的组合形式,从而产生新的可调整的控制点,新的控制点可由原控制点线性组合得到。
基于以上研究,本文进一步得到了新的基函数构造方法,并构造了带参数的三次多项式曲线,此曲线在满足一定条件下达到G1连续。
1 基函数构造原理

零的下三角矩阵。有如下定理。
定理1对定义在[0,1]区间上的由带参数的基函数生成的n次多项式曲线均可由n次Bernstein基生成,转变为控制点带参数的n次Bézier曲线,其中原控制点为m+1个,新控制点为n+1个(m≤n)。
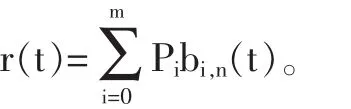

通过上述定理,带参数的多项式基函数的构造方法是由n次Bernstein基乘以矩阵H得到。由b0,n(t),b1,n(t),…,bm,n(t)满足非负性和单位分解性,H需满足如下要求:
(1)H是(n+1)×(m+1)矩阵;
(2)0≤{H}ij≤1;即矩阵里的每个元都是大于等于0小于等于1的;
矩阵H可有下述情形:

可得到m次Bernstein基的n次扩展;

有对称性;
(3)H是非奇异全正矩阵或全正矩阵,得到的基函数具有全正性。
文献[2]中的基函数
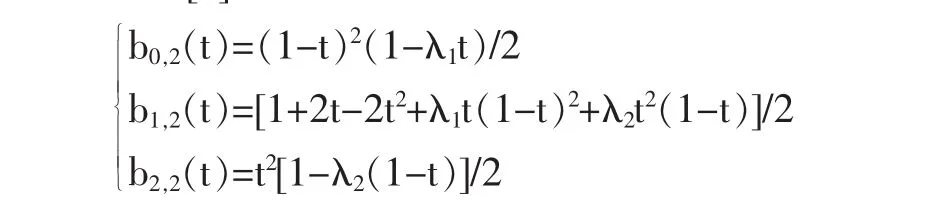
可以看成由3次Bernstein基乘以矩阵H1生成的,其中:

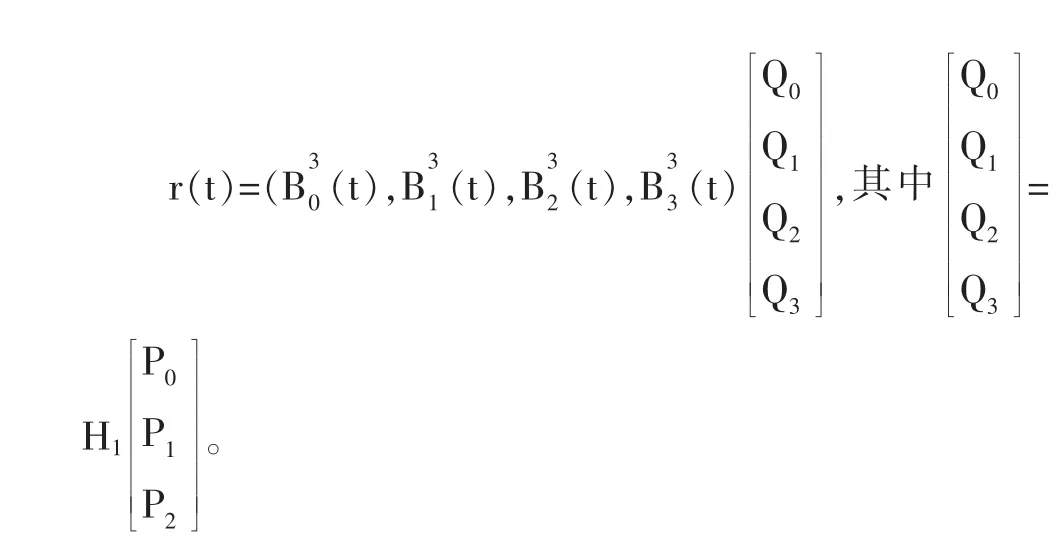
文献[5]中的λ-B样条基可以看成由4次Bernstein基乘以矩阵H2生成的,其中:

2 基函数的定义及其性质

性质1非负性,单位分解性;即bi,2(t)≥0(i=
性质2拟对称性;即当α=β,μ=ν时,(1)式具有对称性;当α≠β,μ≠ν时,(1)式不具有对称性。
性质3退化性;当μ=ν=1,α=λ1,β=λ2时,(1)式退化为文献[2]中当k=2时的基;当μ=ν=1,α=β=0时,(1)式退化为2次均匀B样条基;当μ=ν=1,α=β=λ时,(1)式退化为文献[3]中的基;当μ=ν=-1,α=2(αi-1),β=2(βi-1)时,(1)式退化为文献[4]中的基。
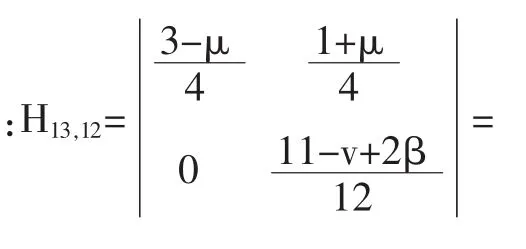
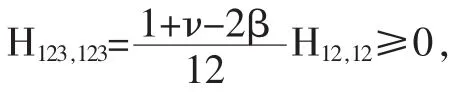
3 曲线的构造及其连续性
给定控制点P0,P1,P2∈Rd(d=2,3),记(1)式中的矩阵为H,令(Q0,Q1,Q2,Q3)=(P0,P1,P2)H',得到4个新的控制点。则有如下曲线定义。
图1给出了当α,β固定时,μ,ν对曲线的影响,其中α=β=-3,曲线由外到内μ,ν的值分别为μ=ν=1,μ= ν=2,μ=ν=3,曲线从不封闭曲线变成了封闭曲线。
图2给出了当μ,ν固定时,α,β对曲线的影响,其中μ=ν=3,曲线由外到内α,β的值分别为α=β=-3,α= β=-2,α=β=-1,α=β=0,随着α,β值增大,封闭曲线所围成的图形面积变小。
图3给出了当μ=ν=-1时,P0=Q0,P2=Q3,曲线插值于首末端点。图3中曲线1、2、3、4、5分别对应α=β= -3,α=β=-2,α=β=-1,α=β=。其中曲线5中Q1,Q2的取值方式如图4中所示,可见它的逼近效果更好[1]。

图1
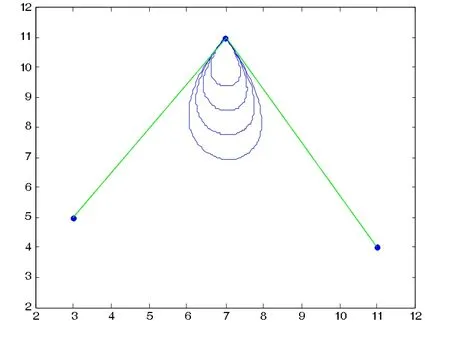
图2
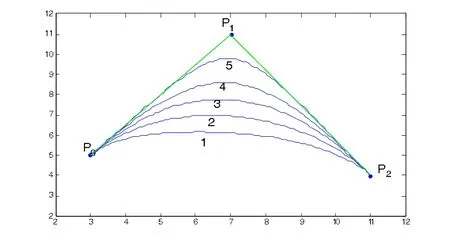
图3
接下来讨论两段曲线的拼接问题。给定4个控制点P0,P1,P2,P3,设2条曲线分别为其中(Q0,Q1,Q2,Q3)=(P0,P1,P2)H';p2(t)=P0,P1,P2,其中(Q4,Q5,Q6,Q7)=(P1,P2,P3)H'。
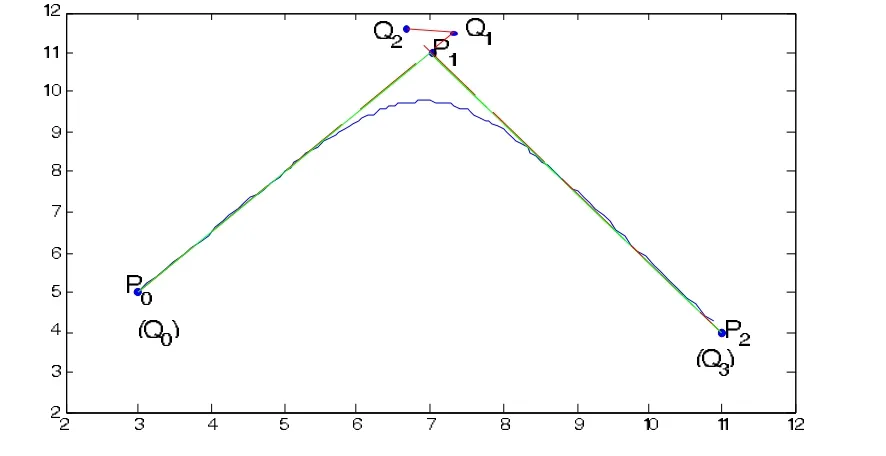
图4
证明:通过计算可得:

将ν=2-μ代入p1(1)得p1(1)=p2(0);(0)=kp1'(1)。证毕。
以下是曲线拼接的实例。
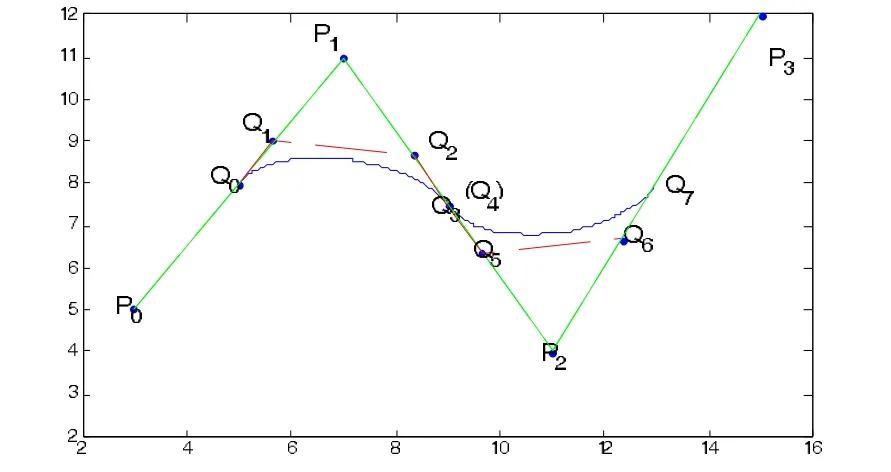
图5 μ=ν=1,α=β=-1
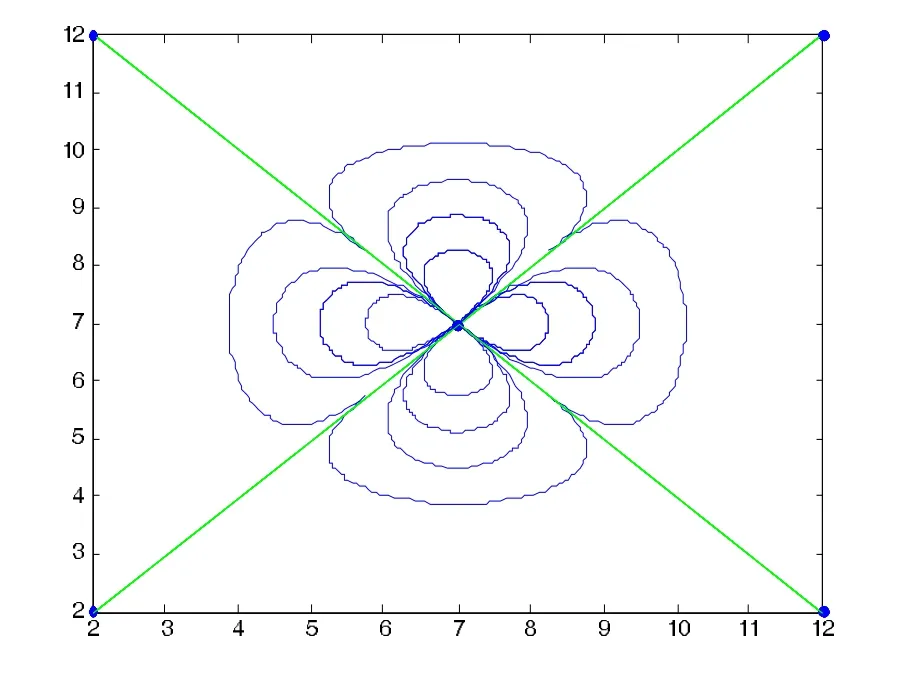
图6 μ=ν=3,α=β=0;μ=ν=3,α=β=-1;μ=ν=3,α=β=-2;μ=ν= 2,α=β=-3

图7 μ=v=3,α=β=0
4 结语
利用本文的基函数构造方法,即能定义Bézier曲线扩展基,又能定义均匀B样条曲线基。利用此法构造的三次带参数的多项式曲线在拼接点处可达到G1连续。
[1]王晶昕,张春梅.调节参数对三角域上Bézier曲面形状的影响[J].辽宁师范大学学报(自然科学版),2011,34(1):6-9.
[2]张莉,邬弘毅.多形状参数的均匀B样条曲线[J].合肥工业大学学报(自然科学版),2007,30(2):252-256.
[3]刘长明,檀结庆.二次均匀B样条曲线的扩展[J].合肥工业大学学报(自然科学版),2004,27(5):459-462.
[4]严兰兰,宋来忠.带两个形状参数的曲Bézier线[J].工程图学学报,2008(3):88-92.
[5]严兰兰,韩旭里.基于全正基的三次均匀B样条曲线的扩展[J].图学学报,2016,37(3):329-336.
[6]X.A.Han,Y.C.Ma,X.L.Huang.A Novel Generalization of Bezier Curve and Surface[J].Journal of Computational and Applied Mathematics,2008,217:180-193.
[7]范菊娴,檀结庆.带多个形状参数的Bézier曲线和曲面[J].合肥工业大学学报(自然科学版),2011,34(1):149-152.
[8]Han Xuli.Piecewise Quartic Polynomial Curves with a Local Shape Parameter[J].Journal of Computational and Applied Mathematics,2006,23(1):34-45.
Discussion of Polynomial Curve with Parameters
XING Qing-dan,CHEN Xue-jiao,PAN Jing
(School of mathematics,Liaoning Normal University,Dalian 116029)
Based on the analysis of the structure principle of the polynomial basis functions with parameters,obtains a new method for the construction of the basis functions.This method is used to construct the three degree polynomial curves with parameters which can be adjusted by the control point,and presents the continuity condition of the curve at the joint point.
Parameter;Polynomial Curve;Basis Function;Continuity
1007-1423(2016)35-0038-05
10.3969/j.issn.1007-1423.2016.35.008
邢庆丹(1991-),女,辽宁东港人,在读硕士,研究方向为函数逼近
2016-11-08
2016-11-28
陈雪娇(1991-),女,辽宁朝阳人,在读硕士,研究方向为计算机辅助几何设计
潘晶(1991-),女,辽宁东港人,在读硕士,研究方向为计算机辅助几何设计

