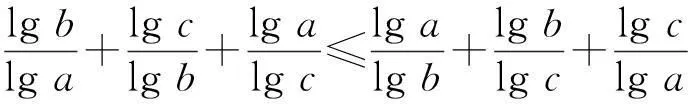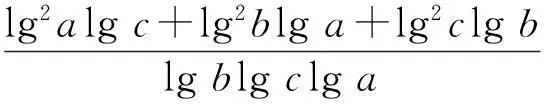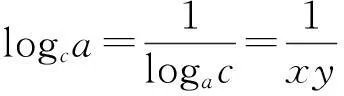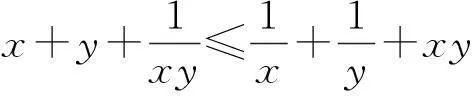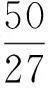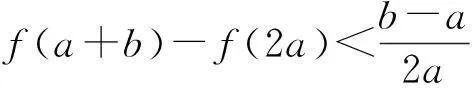借力“联系”观点巧解题



借力“联系”观点巧解题

◇湖北张裕仁向显运

“联系”观点是唯物辩证法中一个很重要的观点.在数学解题思维中,有时就需要我们着眼于活用“联系”观点去分析问题,如此才能迅速找到具体的解题思路.而教学实践又表明，许多学生在解题思维活动中,根本就没有运用“联系”观点去分析、解决问题的思想意识.为此特撷取2011年安徽卷(理科)第19题加以具体说明,以帮助学生拓宽解题思维.

原题(1) 设x≥1,y≥1,证明:

(2) 设1

1) 试题评价.

这是一道比较有趣的不等式问题,而单独的不等式证明题,在近年的高考必考内容中,很少见,是高考的一个冷点.高考命题立意:为了证明一个较复杂的不等式,可以降低难度,先设计一个简单的不等式,当简单不等式获得证明时,再由此证明这个复杂不等式.显然,对考生分析、解决问题的能力提出了较高的要求,需要考生关注这2问之间的紧密联系(即揣摩高考命题意图),并加以灵活运用.

2) 亮点分析.

xy(x+y)≤x+y+x2y2.

因为x+y+x2y2-[xy(x+y)+1]=

x2y2-1-[xy(x+y)-(x+r)]=

(xy+1)(xy-1)-(x+y)(xy-1)=

(xy-1)(x-1)(y-1),

其中x≥1,y≥1,xy≥1,所以上式大于等于0，从而问题得证.

(2)证法1(一般证法)由条件10、lgb>0、lgc>0,所以要证原式成立即证

即证

即证

lg2blgc+lg2clga+lg2algb≤

lg2algc+lg2blga+lg2clgb,

即证

lg2b(lgc-lga)+lg2c(lga-lgb)+

lg2a(lgb-lgc)≤0.

又lgc-lga=-(lga-lgb)-(lgb-lgc),于是通过代入整理知,即证

(lga-lgb)(lg2c-lg2b)+

(lgb-lgc)(lg2a-lg2b)≤0,

从而通过分解因式知,即证

(lga-lgb)(lgb-lgc)(lga-lgc)≤0.

因为1

综上,所求证结论成立.

证法2 (简捷证法)令logab=x,logbc=y,则由1

logac=logab·logbc=xy,

从而,本题即证

其中x≥1,y≥1.由(1)知,上式显然成立，故得证.

3) 感悟体验.

通过上述2种不同的证法,我们能够明显地感觉到“简捷证法”简单、明了,让人耳目一新.其根源就在于,解答第(2)问时注意到了该问与第(1)问之间的紧密联系——外在结构相同(通过观察即知),内在本质一致(借助“换元”的方式即可说明).一般地,若解答题设计多问,则应在解题之初分析解题思路时，就要努力探寻各问之间的关联性,以便简捷求解.

4) 相关链接.

反思这是西安市临潼区某年的一道高考数学模拟检测题,当时阅卷发现全区6000多考生,只有2人做对了第(2)问,大部分考生都是直接针对该问具体分析的,而没有注意到考虑这2问之间的紧密联系,即缺乏活用“联系”观点去分析、解决具体问题的思想意识

5) 巩固练习.

(1) 求直线l的方程及m的值;

(2) 若h(x)=f(x+1)-g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;

(3) 当0

分析第(1)问利用导数可得直线l的方程为y=x-1,m的值为-2.

第(2)问,得到函数h(x)的最大值为2,请注意在此问求解中,又得到函数h(x)=ln(x+1)-x+2在(-1,0)上递增,在(0,+∞)上递减.

由于许多数学解答题设计多问的目的就是降低试题的难度,而各问之间又往往存在着某种紧密的联系,因此将“联系”的观点灵活运用于数学解题活动中,往往能出奇制胜,得到简捷、明了的解(证)过程.

(作者单位：湖北省当阳市第二高级中学)