区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的构造

乔希民， 吴洪博

(1. 商洛学院 数学与计算机应用学院， 陕西 商洛 726000； 2.陕西师范大学 数学与信息科学学院， 陕西 西安 710062)



乔希民1， 吴洪博2

(1. 商洛学院 数学与计算机应用学院， 陕西 商洛 726000； 2.陕西师范大学 数学与信息科学学院， 陕西 西安 710062)

摘要：以区间集和滤子理论作为研究区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的工具，通过引入区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的概念，讨论了生成〈∈,∈Q〉-fuzzy滤子的几种方法，彰显模糊逻辑推演系统被视为代数滤子的镜像.

关键词：非可换模糊逻辑； 区间集； 区间集上非交换剩余格； 〈∈,∈Q〉-fuzzy滤子；构造性方法

QIAO Ximin1, WU Hongbo2

(1.CollegeofMathematicsandComputerApplication,ShangluoUniversity,Shangluo726000,ShaanxiProvince,China; 2.CollegeofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi’an710062,China)

0引言

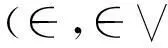
本文试图将区间集思想和滤子理论运用到非交换剩余格,引入区间集上非交换剩余格的概念,在模糊点和模糊集间的“属于关系”中析取“拟重于关系”，将其拓展为“属于关系”广义析取()“权拟重于关系”(Q)，给出区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的定义，并研究〈∈,∈Q〉-fuzzy滤子的基本性质，进一步探讨区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的构造方式和完备性,以从本质上认识〈∈,∈Q〉-fuzzy滤子的基本特征.

1预备知识

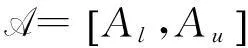
设U为论域,2U是U的幂集,那么区间集上2U的子集形式为：

称其为闭区间集.闭区间上的所有区间集的集合记为

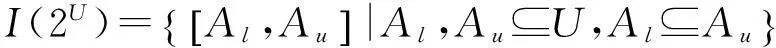
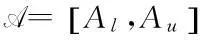
引理1[21]设A,B,C∈I(2U),则下列各式成立:

定义3设〈I(2U),,,⊗,⟹,,U,∅〉是一个(2,2,2,2,2,0,0)型代数，若满足以下条件:

(Ⅰ)〈I(2U),,,U,∅〉是一个有界格；

(Ⅱ)〈I(2U),⊗,U〉是以U为单位元的半群；

定义4若I(2U)中的算子⊗满足交换性,则称I(2U)为区间集上交换剩余格.

性质1设I(2U)是一个区间集上非交换剩余格,∀X，Y,Z∈I(2U),则有以下性质成立：

(1) ⊗:I(2U)×I(2U)→I(2U)是单调递增的；

可直接运用定义3与文献[21]的相关定理完成上述性质的证明.

定义5设I(2U)是区间集上非交换剩余格,Φ≠J⊆I(2U),如果∀X，Y∈I(2U),有

(2)若X，Y∈I(2U)，则X⊗Y∈I(2U)，那么称J为I(2U)上的一个滤子，所有滤子之集记为J(I(2U)).

又若J是I(2U)的一个滤子，且满足：∀X，Y,XYJ,可推出XJ或YJ,则称J是I(2U)的素滤子.

(1)U∈J；

定义6设I(2U)是区间集上非交换剩余格,G:I(2U)→[∅,U]是一个映射，则G为I(2U)的模糊子集.全体模糊子集之集记为F(I(2U)).

定义7设I(2U)是区间集上非交换剩余格,

J∈F(I(2U)),∀T∈[∅,U],

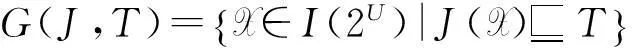
则称G(J,T)是I(2U)上的T-水平集.

定义8设I(2U)是区间集上非交换剩余格,X∈I(2U),J∈F(I(2U)),若J满足:

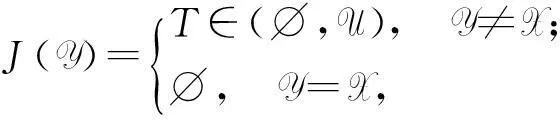
则称J为I(2U)上的一个模糊值,记为XT,其中X是XT的支撑,T为XT的值，记为G(X,T).

注2P(X)⊕T表示P(X)与T的线性和；P(X)⊖T表示P(X)与T的线性差.

定义9设I(2U)是区间集上非交换剩余格,∀X，Y∈I(2U),J∈F(I(2U)),如果J满足以下条件:

则J称之为I(2U)上的fuzzy滤子.全体fuzzy滤子之集记为JJ(I(2U)).

命题2设I(2U)是一个区间集上的非交换剩余格,J∈F(I(2U)),则J是I(2U)上一个fuzzy滤子的充要条件为

定义10设I(2U)是区间集上非交换剩余格,P∈F(I(2U)),∀T,R∈(∅,U),如果P满足以下条件:

定理1设I(2U)是区间集上非交换剩余格,F∈F(I(2U)),则F为〈∈,∈Q〉-fuzzy滤子的充要条件是F满足(FP3)和(FP4),其中,

(FP4) ∀X，Y∈I(2U),

证明首先,证明(FP1)等价于(FP3),即以下2种情形成立.

(1)若有(FP1),则有(FP3).

(2)证明若有(FP3),则有(FP1).

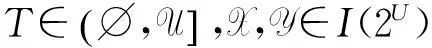
其次,证明(FP2)等价于(FP4),即以下2种情形成立.

(1)若有(FP2),则有(FP4).

(2)若有(FP4),则有(FP2).

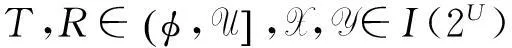
综上,证得定理1成立.

推论1设I(2U)是区间集上非交换剩余格,若F是I(2U)上的fuzzy滤子,则F是I(2U)上的〈∈,∈Q〉-fuzzy滤子.

推论2设I(2U)是区间集上非交换剩余格,若F是I(2U)上的〈∈,∈Q〉-fuzzy滤子,且F(U)CI,则F是I(2U)上的fuzzy滤子.

定义12设I(2U)是区间集上非交换剩余格,F∈F(I(2U)),G∈FF(I(2U))，若有

(1)F⊆G；

(2) ∀H∈FF(I(2U))，如果F⊆H，那么G⊆H,则称G是I(2U)上由F构造的〈∈,∈Q〉-fuzzy滤子，记为[F].

命题3设∀F,G∈F(I(2U)),则有

(1)如果F∈FF(I(2U)),那么F=[F]；

(2)如果F⊆G，那么[F]⊆[G].

由定义12容易证得.

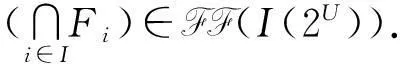
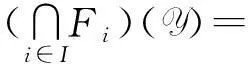
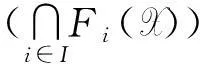
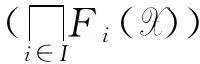
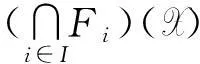
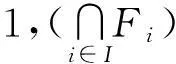
推论3设I(2U)是区间集上非交换剩余格,F1,F2∈FF(I(2U)),则F1∩F2∈FF(I(2U)),但F1∪F2未必是I(2U)上的〈∈,∈Q〉-fuzzy滤子.

定理2设F∈F(I(2U)),则∀X∈I(2U),

[F](X)={F(A1)F(A2)…F(An)

i=1,2,…,n}F(X).

证明若∀X∈I(2U),则

G(X)={F(A1)F(A2)…F(An)

i=1,2,…,n}CI.

G(X)={F(A1)F(A2)…F(An)

Ai∈I(2U),i=1,2,…,n}.

(1)证G是〈∈,∈Q〉-fuzzy滤子.设X，Y∈I(2U),

A1⊗A2⊗…⊗An;Ai∈I(2U),i=1,2,…,n}，

B2⊗…⊗Bm;Bj∈I(2U),j=1,2,…,m}，

C1⊗C2⊗…⊗Ct;Cp∈I(2U),p=1,2,…,t}.

分2步完成(1)的证明:

同样,(FP3)成立.

分2种情形:

A1⊗A2⊗…⊗An⊗B1⊗B2⊗…⊗Bm;

Ai,Bj∈I(2U),i=1,2,…,n,j=1,2,…,m}=

Cp∈I(2U),p=1,2,…,t}=G(X⊗Y),

证得定理1之(FP4)成立.

G(X)=F(X),G(Y)=F(Y),

综上可知,G是I(2U)上的〈∈,∈Q〉-fuzzy滤子.

(2)设H∈FF(I(2U)),且F⊆H.因为∀X∈I(2U),

G(X)={F(A1)F(A2)…F(An)CI|XA1⊗A2⊗…⊗An;Ai∈I(2U),i=1,2,…,n}F(X){H(A1)H(A2)…H(An)CI|XA1⊗A2⊗…⊗An,Ai∈I(2U),i=1,2,…,n}H(X)=H(X),

所以G⊆H.

又因为F⊆H,故依据定义12，知G是由F构造的〈∈,∈Q〉-fuzzy滤子.

推论4设I(2U)是区间集上非交换剩余格,F∈F(I(2U)),则有∀X∈I(2U),

[F](X)={F(A1)F(A2)…F(An)CI|

A1⟹(A2⟹…⟹(An⟹X)…)=U;

Ai∈I(2U),i=1,2,…,n}F(X)={F(A1)F(A2)…

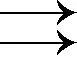
i=1,2,…,n}F(X).

定理3设I(2U)是区间集上非交换剩余格,F,G∈FF(I(2U)),∀x∈I(2U),则

[F∪G](X)={F(A)G(B)CI|XA⊗B,

A,B∈I(2U)}F(X)G(X).

证明设X∈I(2U)，根据定理2知

[F∪G](X)={(F(A1)G(A1))…

A1⊗A2⊗…⊗An;Ai∈I(2U),

i=1,2,…,n}F(X)G(X).

(1)若X∈I(2U)，则有

(2)若X∈I(2U)，则

{(F(T1)(G(T1))…(F(Tn)G(Tn))CI|

Ti∈I(2U),i=1,2,…,n}=

{(F(A1)G(A1))…(F(An)

G(A1)(i=1,2,…,n),

B1⊗B2⊗…⊗Bm;Ai,Bj∈I(2U),

i=1,2,…,n,j=1,2,…,m}∪

{F(C1)G(C1)…(F(Cn)G(Cn))

Ci∈I(2U),i=1,2,…,n}∪

{(F(D1)G(D1))…(F(Dm)

Dj∈I(2U),j=1,2,…,m}.

若令

A={(F(A1)G(A1)…(F(An)G(An))

(F(B1)G(B1))…(F(Bm)G(Bm))CI|

Ai,Bj∈I(2U),i=1,2,…,n,j=1,2,…,m},

B={(F(C1)G(C1))…(F(Cn)G(Cn))CI|

Ci∈I(2U),i=1,2,…,n},

C={(F(D1))G(D1))…(F(Dm)

Dj∈I(2U),j=1,2,…,m},

则有

[F∪G](X)=(A)(B)(C)F(X)G(X),

再设

A=A1⊗A2⊗…⊗An∈I(2U),

B=B1⊗B2⊗…⊗Bm∈I(2U),

又因为

所以

A,B∈I(2U)}F(X)G(X).

这样,由(1)、(2)可知：

[F∪G](X)=

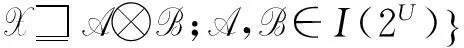
(2)F(GH)=(FG)(FH).

下面从两方面考虑(1)的证明.

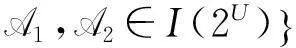
A1,A2∈I(2U)})][F(X)G(X)]

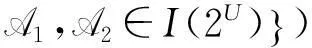
B1,B2∈I(2U)})(FG)(X)(FH)(X)

又因为X具有任意性,所以

由以上2步可知(1)成立.

同理可证(2)也成立.

4结语

基于非可换模糊逻辑背景,引入了区间集上非交换剩余格与区间上非交换剩余格fuzzy滤子的概念,给出了区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的代数结构,进一步讨论了区间集上非交换剩余格-fuzzy滤子的构造概念和代数结构形式.在此基础上,研究了几种生成区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子,并探讨了全体fuzzy滤子集上完备的分配格，以显示区间集上非交换剩余格〈∈,∈Q〉-fuzzy滤子的特征和性质.对于区间集上非交换剩余格广义fuzzy滤子及其相应特殊广义fuzzy滤子,以及如何建立区间集上相应模糊逻辑系统等将另文探讨.

参考文献(References)：

[1]ZADEH L A. Fuzzy sets[J]. Information and Control,1965，8(3):338-353.

[2]胡宝清.模糊理论基础[M]. 第2版，武汉:武汉大学出版社,2010.

HU Baoqing. Fuzzy Theory Foundation[M]. 2nd ed, Wuhan:Wuhan University Press,2010.

[3]胡启洲,张卫华.区间数理论的研究及其应用[M].北京:科学出版社,2010.

HU Qizhou,ZHANG Weihua. Study and Application of Interval Number Theory[M].Beijing ：Science Press, 2010.

[4]YAO Yiyou. Interval sets and interval-set algebras[C]//The 8th IEEE International Conference on Cognitive Informatics. Hong Kong: IEEE Computer Society,2009:307-314.

[5]姚一豫.区间集[C]//王国胤,李德毅, 姚一豫,等.云模型与粒计算.北京:科学出版社,2012:74-93.

YAO Yiyu. Interval sets[C]//WANG Guoyin,LI Deyi,YAO Yiyu，et al. Cloud Model and Granular Computing. Beijing ：Science Press, 2012:74-93.

[6]YAO Y Y. Two views of theory of rough sets in finite universes[J]. International Journal of Approximation Rersoning,1996,15(4):291-317.

[7]胡宝清.基于区间集的三支决策粗糙集[C]//刘盾，李天瑞，苗夺谦，等.三支决策与粒计算.北京：科学出版社，2013：163-195.

HU Baoqing. Three-way decisions rough sets on interval sets[C]//LIU Dun, LI Tianrui, MIAO Duoqian,et al. Three-way Decisions and Granular Computing. Beijing:Science Press,2013:163-195.

[8]LIN L Z., LI K T. Boolean filters and positive implicative filters of residuated lattices[J]. Information Sciences,2007,177(24):5725-5738.

[9]WANG Z D, FANG J X . Onv-filters and normalv- filters of a residuated lattice with a weakvt-operator[J].Information Sciences, 2008,178:3465-3473.

[10]ZHAN J M, XU Y. Some types of generalized fuzzy filters of BL-algebras[J]. Computers and Mathematics with Applications, 2008,56(16):1640-1616.

[11]王国俊. 非经典数理逻辑与近似推理 [M]. 第2版，北京:科学出版社, 2008.

WANG Guojun. Nonclassical Mathematical Logic and Approximate Reasoning[M]. 2nd ed, Beijing：Science Press,2008.

[12]裴道武.基于三角模的模糊逻辑理论及其应用[M].北京:科学出版社,2013.

PEI Daowu. Based on the Triangle Model of Fuzzy Logic Theory and Its Application [M].Beijing：Science Press,2013.

[13]ROSENFELD A. Fuzzy groups [J]. Journal of Mathematical Analysis and Applications,1971,35:512-517.

[14]BHAKAT S K, DAS P. On the definition of a fuzzy subgroup[J]. Fuzzy Sets Systems,1992,51:235-241.

[15]BHAKAT S K,DAS P.〈∈,∈vq〉-fuzzy subgroup[J]. Fuzzy Sets Systems,1996,80:359-368.

[16]BHAKAT S K, DAS P. Fuzzy subrings and ideals redefined[J]. Fuzzy Sets Systems,1996,81:383-393.

[17]PU P M, LIU Y M. Fuzzy topologyⅠ:Neighborhood structure of a fuzzy point and moore-smith convergence[J]. Journal of Mathematical Analysis and Applications,1980,76(2):571-599.

[18]PU P M, LIU Y M. Fuzzy topologyⅡ:Product and quotient spaces[J]. Journal of Mathematical Analysis and Applications,1980,77(2):20-37.

[19]LIAO Z H, CU H.〈∈,∈∨q(λ,μ)〉-fuzzy normal subgroup[J]. Fuzzy Systems and Mathematics,2006,20(5):47-53.

[20]YUAN X H, ZHANG C, REN R H. Generalized fuzzy subgroups and many-valued implications[J]. Fuzzy Sets and Systems,2003,138:205-211.

[21]乔希民,张东翰. 区间集上R0-代数的表示形式及其性质[J].重庆工商大学学报:自然科学版,2014，31(9):15-21.

QIAO Ximin, ZHANG Donghan. The representation and properties ofR0-algebra on interval sets[J]. Journal of Chongqing Technology and Business University: Natural Science Edition,2014,31(9):15-21.

Abstract:Based on interval sets and the filter theory, the non-commutative residual lattice 〈∈,∈Q〉-fuzzy filter on the interval sets was researched. Firstly, we introduced the structural concept of the non-commutative residual lattice 〈∈,∈Q〉-fuzzy filter on the interval sets, and then discussed several methods for generating 〈∈,∈Q〉-fuzzy filter. Fuzzy logic deduction system is regarded as the acoustic image of algebraic filter.

Key Words:non-commutative fuzzy logic; interval sets; non-commutative residual lattice on interval sets; 〈∈,∈Q〉-fuzzy filter; constructional method

中图分类号：O 141

文献标志码：A

文章编号：1008-9497(2016)02-127-07

DOI:10.3785/j.issn.1008-9497.2016.02.001

作者简介：乔希民(1960-),ORCID:http://orcid.org/0000-0002-9585-672X,男,副教授,硕士,主要从事非经典数理逻辑与格上拓扑学研究,E-mail：qiaoximin@163.com.

基金项目：国家自然科学基金资助项目(61572016)；陕西省自然科学基础研究计划项目(2013JM1023)；陕西省教育厅科研计划项目(11JK0512).

收稿日期：2015-03-01.