与特殊四边形相关的热点问题

宋志娟



与特殊四边形相关的热点问题

宋志娟

本章探究的是平行四边形以及特殊平行四边形的相关知识，重点是分清不同四边形的区别与联系，理解和掌握它们的定义、性质及判定方法.这部分内容在中考中经常出现，下面我们通过例子说明解决这类问题的方法.

一、与概念相关的问题

例1已知四边形ABCD，有以下四个条件：①AB∥CD；②AB=CD；③BC∥AD；④BC=AD.从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（）.

A. 6种B. 5种C. 4种D. 3种

【分析】从四个条件可以知道，条件中只涉及四边形的对边相等和平行.根据对边关系判定平行四边形有以下3种方法：

（1）两组对边分别平行的四边形是平行四边形；

（2）两组对边分别相等的四边形是平行四边形；

（3）一组对边平行且相等的四边形是平行四边形.

满足（1）的有①③，满足（2）的有②④，满足（3）的有①②或③④，所以一共有4种选法.

【点评】当被研究的问题有可能出现多种情况时，我们必须按可能出现的情况不重复不遗漏地进行分类讨论.

二、与折叠相关的问题

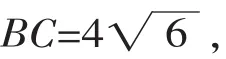
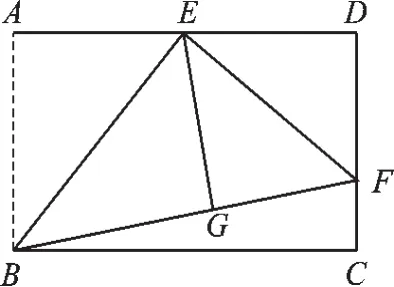
图1

【分析】根据点E 是AD的中点以及翻折的性质，我们有AE= DE=EG，可以证得△EDF和△EGF全等，根据全等三角形对应边相等可得DF=GF.设FD=x，则可用x表示出FC、BF，在Rt△BCF中，利用勾股定理建立方程即可得其解.

解：∵E是AD的中点，

∴AE=DE，

∵△ABE沿BE折叠后得到△GBE，

∴AE=EG，AB=BG，

∴ED=EG，

∵在矩形ABCD中，

∴∠A=∠D=90°，

∴∠EGF=90°，

∵在Rt△EDF和Rt△EGF中，

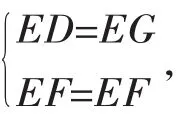
∴Rt△EDF≌Rt△EGF（HL），

∴DF=FG，

设DF=x，则BF=6+x，CF=6-x，

解得x=4.

∴DF=4.

【点评】由折叠对应得到对应角相等，对应线段相等，由此得到两个三角形全等，再运用勾股定理建立方程，是解决这类问题常用的方法.

三、与最值相关的问题

例3如图2，在正方形ABCD中，点E 在BC上，BE=3，CE=2，点P在BD上，求PE+ PC的最小值.

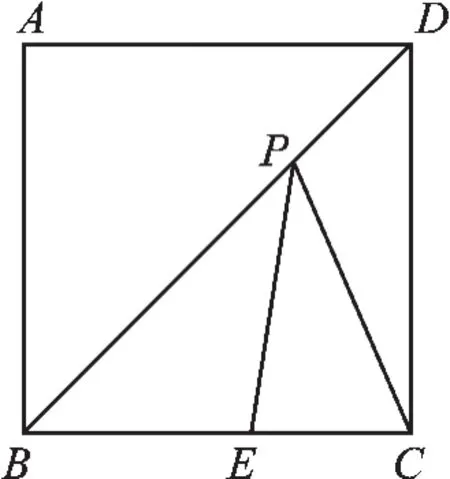
图2

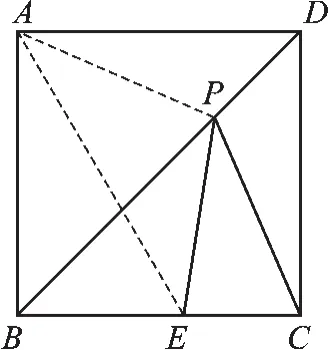
图3

【分析】由于PE、PC的值均不能直接求出，要求PE+PC的最小值，可考虑通过作辅助线将PE或PC转化为与其相等的线段，利用相关定理找出PE+PC的最小值.

解：如图3，连接AE、AP，

∵点C关于BD的对称点为点A，

∴PE+PC=PE+AP，

根据两点之间线段最短可得AE就是AP+PE的最小值，

∵正方形ABCD的边长为5，BE=3，

【点评】正方形是轴对称图形，借助其轴对称性可以巧妙地解决一些与正方形有关的问题.当然这个题目的背景还可以换为菱形.解决这类问题的一般思路是利用对称性，借助转化，建立“两点之间，线段最短”的几何模型.

四、与动点相关的问题

例4如图4，在矩形ABCD中，AB=4 cm，AD=12 cm，点P在AD边上以每秒1 cm的速度从点A向点D运动，点Q在BC边上，以每秒4 cm的速度从点C出发，在CB间往返运动，两点同时出发，当点P到达点D时停止（同时点Q也停止）运动，设运动的时间为t秒，当t为何值时PQ∥AB.

图4

【分析】点P从点A到达点D需12秒，所以点Q需在B、C间往返两次，而在每次的运动过程中都有一次PQ∥AB，根据AD∥BC，PQ∥AB，可知四边形APQB是平行四边形，则PA=BQ，列方程求解即可得到所需时间.

解：∵四边形ABCD是矩形，

∴AD∥BC，

若PQ∥AB，

则四边形APQB是平行四边形，

∴AP=BQ，

①当0≤t＜3时，

设过了t秒，PQ∥AB，则PA=t，BQ=12-4t，

∴t=12-4t，

解得：t=2.4（s），

②当3≤t＜6时，

PA=t，BQ=4t-12，

∴t=4t-12，

解得：t=4（s），

③当6≤t＜9时

PA=t，BQ=36-4t，

∴t=36-4t，

解得：t=7.2（s），

④当9≤t≤12时，

PA=t，BQ=4t-36，

∴t=4t-36，

解得：t=12（s）.

∴当t=2.4、4、7.2、12秒时PQ∥AB.

【点评】在分析过程中，要特别关注图形的特性，寻找合理的代数关系式，确定运动变化过程中的数量关系和图形的位置关系，这样就能找到解决问题的途径.