基于有理正交系对有理解析信号的分解算法研究
杨国亮,谭立辉,史晓霞
(广东工业大学应用数学学院,广东广州510520)
基于有理正交系对有理解析信号的分解算法研究
杨国亮,谭立辉,史晓霞
(广东工业大学应用数学学院,广东广州510520)
摘要:对LPSD算法进行改进,引入有理正交基来替换原来的三角函数基。与三角函数基相比,有理正交基的优势是能自适应地选取基函数的系数。采用能量下降最快的思想和最小均方误差思想逐步求得基函数的系数,然后分解出极小相位信号与全相位信号。与LPSD算法相比,改进后算法比之前在耗时与算法迭代步数上有很大改进,信号拟合效果更好。
关键词:有理解析信号;极小相位;全相位;有理正交系
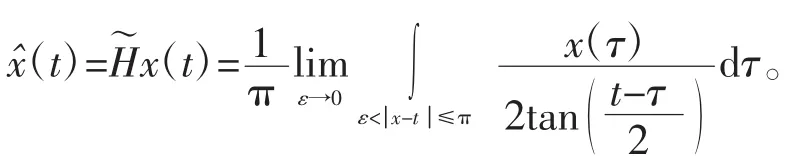
文献[3-4]指出,任意一个周期解析信号s(t)∈Lp[-π,π](1≤p≤∞)都可以分解为极小相位信号(MinP)与全相位信号(AllP)的乘积,其中极小相位信号能在一个常数误差范围内由其幅度或者相位完全重构出来,而全相位信号的瞬时频率是非负的。对于具有有限带宽的多项式周期解析信号可表示为
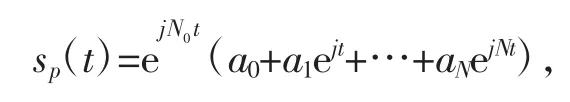
其中N0为非负整数,a0≠0和aN≠0。将其分解为极小相位和全相位信号的算法有很多种,第1种方法是求根法,即求出s(pz)=zN(0a0+a1z+…+aNzN)所有的根,然后将其分解出极小和极大相位;第2种方法是先计算信号s(pt)的对数幅度,然后通过周期Hilbert变换计算出其极小信号的相位,并用s(pt)的相位减去,获得相应的全相位信号的相位。
R Kumaresan等用一种新的LPSD算法[5-6]来提取周期解析信号的极小相位信号(MinP)和全相位信号(AllP),其算法流程图如图1所示。
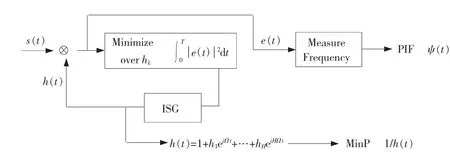
图1 LPSD算法
在图1中,包含一个相乘器或调制器,一个逆信号发生器(ISG),还有一个误差最小模块。该算法的主要思想是周期多项式解析信号sp(t)与逆信号h(t)相乘,得到误差信号e(t),通过选择合适的系数hk,使得e(t)的能量最小,即

1 有理解析信号的分解及算法实现
1.1有理周期解析信号的分解
作为解析信号的一种特殊情况,有理周期解析信号也可以分解为极小相位信号与全相位信号的乘积。为了更清楚地描述出其结构特征,下面给出更具体的分析。考虑一个周期为2π且在单位圆周上没有零点的有理解析信号为

1.2算法过程
首先给出推广的LPSD算法在计算机上实现的具体过程,即如何实现下面的误差能量最小化
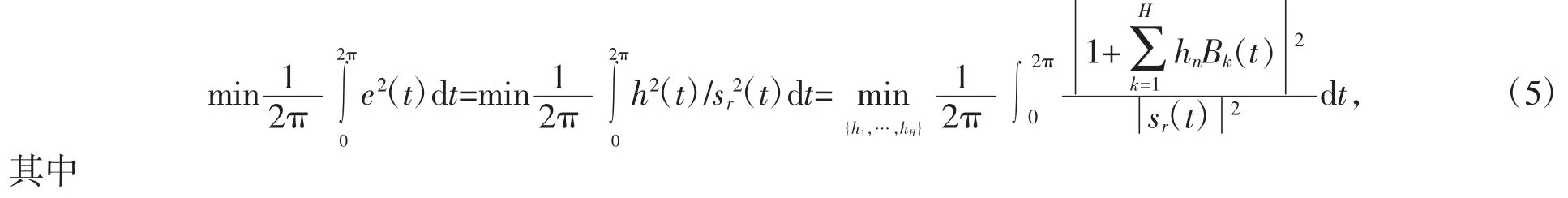

1.3算法实验
笔者运用推广的LPSD算法再来分解有理解析信号,本实验是在MATLAB7.0[11-12]上完成的,取有理解析信号为

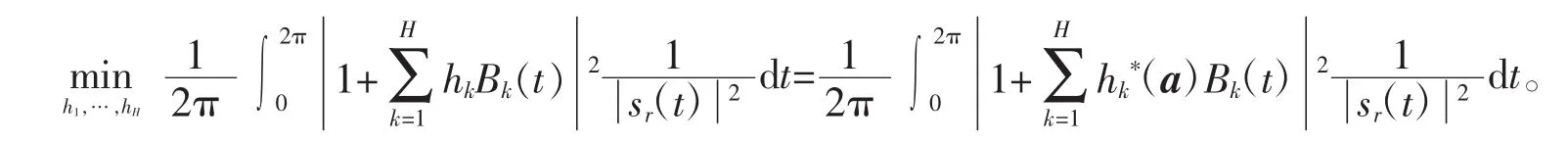
比如说,在算法中取所有的ak=0,k=1,2…,H,则此方法就退化到R Kumaresan等[5]于1998年给出的LPSD算法。在LPSD算法下,取h(t)的系数H=60,实验结果如图2、3所示。
图2 原信号与LPSD算法的极小相位信号的幅度对数及误差信号的幅度

图3 LPSD算法的全相位信号正的瞬时频率与原信号瞬时频率
图2中,“重构”对应的线条是用LPSD算法重构得到的极小相位信号的幅度对数,“原来”对应的线条为原信号的幅度对数,“误差”对应的线条为误差信号的幅度,从图2中可以看出,用LPSD算法重构得到的曲线和原来的曲线基本上重合了,两者的误差很小。图3中,“PIF”对应的线条为全相位信号的瞬时频率,“IF”对应的线条为原信号的瞬时频率。
虽然LPSD算法也能将有理解析信号很好地分解为极小相位信号和全相位信号的乘积,但此方法有一个缺陷,就是{a1,a2,…,aH}⊂D必须事先给定,不能自适应地选取。针对这种不足,有两种解决办法,一种是全局最优地选取{a1,a2,…,aH}⊂D,即
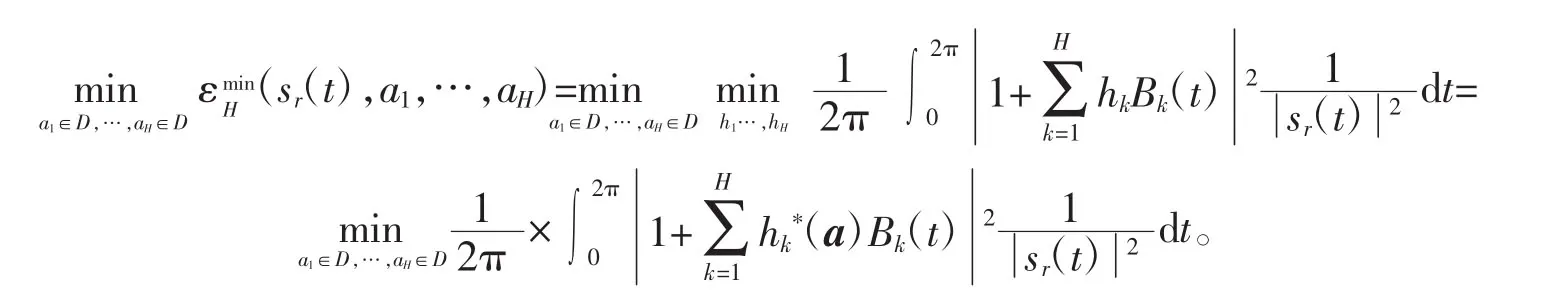
但这种方法的缺点是:在耗时方面和算法迭代步数上,需花费更多,主要是因为在求系数a1,…,aH时,需要嵌套H个循环求出所有的能量值。为了改进这种缺陷,笔者用逐步选取最优的思路来解决,即第2种解决方法,分步思想为:

〈H〉当为H时,基为:B1(t)、…、BH(t),把上H-1步求得的,这时只有一个未知数aH,最后利用最小均方误差方法求最小能量,即
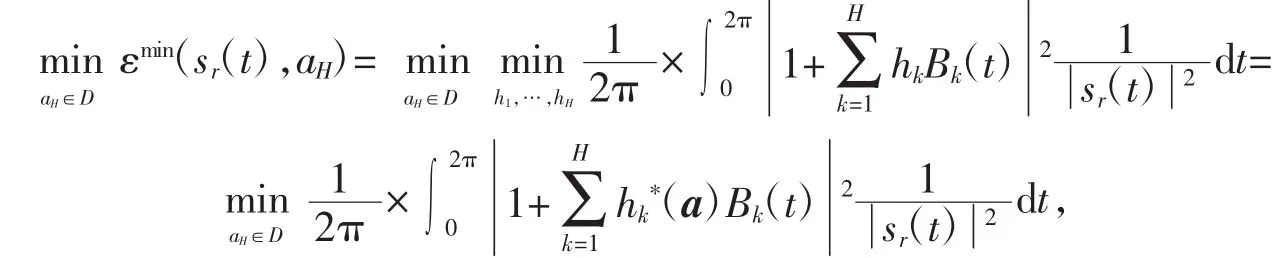
从而得到aHmin。把每一步求得的系数am1in、…、aHmin代入B(1t)、…、B(Ht),即可求出有理正交基。使得误差信号e(t)=h(t)/s(rt)的能量达到最小,满足表达式(7),即可得到解向量,再把代入h[n]中,就可以得到。所以,s(t)极小相位信号sMinP[n]等于h[n],全相位信号e[n]则等于h[n]/sr[n]。
取h(t)的系数H=3,实验结果如图4、5所示。
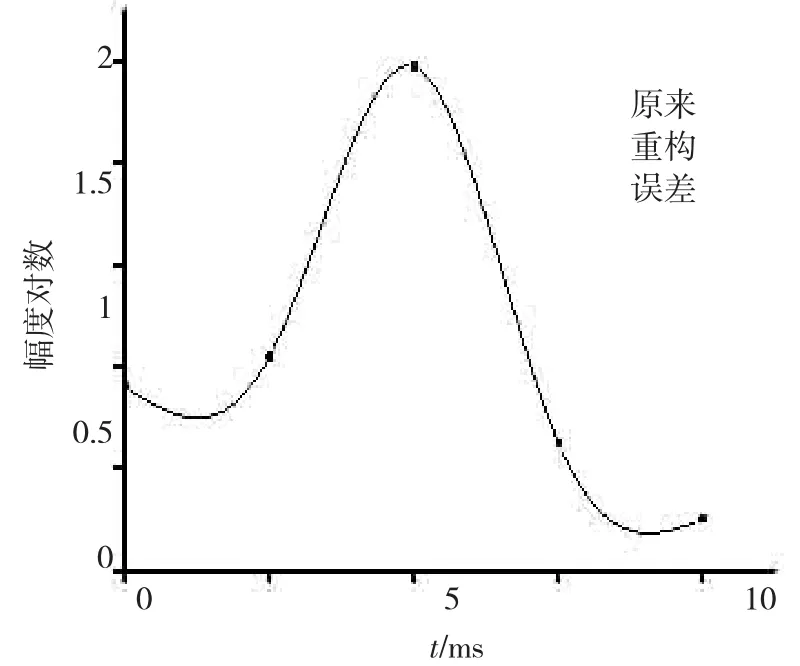
图4 原信号与改进LPSD算法的极小相位信号的幅度对数及误差信号的幅度
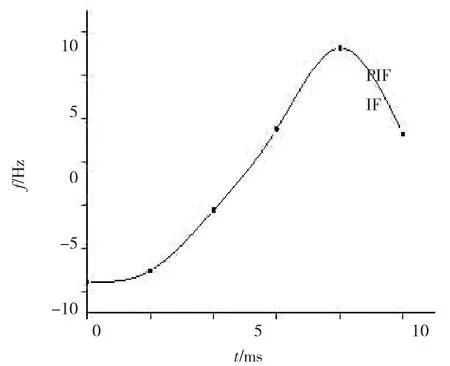
图5 改进LPSD算法的全相位信号正的瞬时频率与原信号瞬时频率
图4中,“重构”对应的线条为基于改进LPSD算法重构得到的极小相位信号的幅度对数,“原来”对应的线条为原信号的幅度对数,“误差”对应的线条为误差信号的幅度,从图4中可以看出,用基于改进LPSD算法重构得到的曲线与“原来”的曲线相比,LPSD算法拟合得更好,两者的误差也更小。图5中,“PIF”对应的线条为基于改进LPSD算法的全相位的频率,“IF”对应的线条为原信号的频率,用基于改进LPSD算法得到的曲线相比LPSD算法更光滑。
2 结语
本文利用R Kumaresan等提出的LPSD算法,对有理解析信号进行分解,从而得到极小相位信号和全相位信号。为了改进和推广LPSD算法,笔者引入有理正交基来替换原来的三角函数基,并采用分步最优思想求有理正交基的系数a1,…,aH。与LPSD算法相比,改进后算法比之前在耗时与算法迭代步数上有很大改进,信号拟合效果更好。
参考文献:
[1]刘树棠,黄建国.离散时间信号处理[M].西安∶西安交通大学出版社,2001.
[2]LEON C. Time-Frequency Analysis[M]. Englewood Cliffs,NJ∶Prentice Hall,1995.
[3]QIAN T. Boundary derivatives of the phases of inner and outer functions and applications[J]. Mathematical Method in the Applied Sciences,2009,32(3)∶253-263.
[4]TAN L H,YANG L H,HUANG D R. The structure of instantaneous frequencies of periodic analytic signals[J]. Science China Mathematics,2010,53(2)∶347-355.
[5]KUMARESAN R,RAO A. Algorithm for decomposing an analytic signal into AM and positive FM components[C]// Proceedings of the 1998 IEEE International Conference. Piscataway,NJ,USA∶IEEE Press,1998∶1561-1564.
[6]KUMARESAN R,ALLU G K,SWAMINATHAN J,et al. Decomposition of a bandpass signal and its applications to speech processing[C]//Conference Record of the Thirty-Seventh Asilomar Conference. Piscataway,NJ,USA∶IEEE Press,2004∶2078-2082.
[7]KUMARESAN R,RAO A. Model-based approach to envelope and positive instantaneous frequency estimation of signals with speech applications[J]. The Journal of the Acoustical Society of America,1999,105(3)∶1912-1924..
[8]HUANG N E,SHEN Z,LONG S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society,1998,454(1971)∶903-995.
[9]QIAN T,WANG Y B,DANG P. Adaptive Decompositon into Mono-Components[J]. Advances in Adaptive Data Analysis,2009,1(4)∶703-709.
[10]QIAN T,ZHANG L,LI Z. Algorithm of adaptive Fourier decomposition[J]. Signal Processing,IEEE Transactions on,2011,59 (12)∶5899-5906.
[11]胡广书.数字信号处理理论算法与实现[M].北京∶清华大学出版社,2003.
[12]刘卫国. MATLAB程序设计教程[M].北京∶中国水利水电出版社,2005.
【责任编辑:王桂珍foshanwgzh@163.com】
Research on the decomposition algorithm of rational analytic signal based on rational orthogonal system
YANG Guo-liang,TAN Li-hui,SHI Xiao-xia
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)
Abstract∶We improve the LPSD algorithm by introducing the rational orthogonal basis to replace the trigonometric series. Compared with trigonometric series,the advantage of the rational orthogonal basis is that the coefficients of basis function can adaptively be chosen. In this paper,based on the energy decrease fastest method and the least mean square error method,we can choose the coefficients of basis function step by step. Compared with the LPSD algorithm,the improved algorithm has greatly improved the time consuming and the number of iteration steps. Moreover,the fitting effect is better than that of LPSD algorithm.
Key words∶rational analytical signal;minimal phase;all phase;rational orthogonal system
中图分类号:TN911.6
文献标志码:A
文章编号:1008-0171(2016)03-0011-07
收稿日期:2015-11-16
基金项目:国家自然科学基金资助项目(61471132);广东省优秀青年教师项目(Yq2014060)
作者简介:杨国亮(1989-),男,江西井冈山人,广东工业大学硕士研究生。

