一类Kirchhoff方程最小能量变号解的存在性

郭　红

(山西大学 数学科学学院，山西 太原 030006)



一类Kirchhoff方程最小能量变号解的存在性

郭红

(山西大学 数学科学学院，山西 太原 030006)

摘要:研究一类Kirchhoff方程最小能量变号解的存在性, 其中非线性项满足指数增长.首先用Brouwer不动点定理证明M是非空的, 其次寻找能量泛函在M中的极小值点, 最后应用形变引理证明极小值点就是方程的最小能量变号解.方程中由于非局部项的出现导致通常的变分方法不再适用，因此将方程对应的能量泛函限制在M上, 最终得到了方程变号解的存在性结果.

关键词:Kirchhoff方程;Brouwer不动点定理;形变引理;变号解;最小能量

0引言

本文考虑Kirchhoff方程

(1)

变号解的存在性, 其中Ω是R2中有界光滑区域,a,b>0是常数. 非线性项f满足下面条件:

(f1) 对每个β>0, 存在一个正数Cβ,使得|f(t)|,|f′(t)|≤Cβexp(βt2),t∈R；

近年来,Kirchhoff方程

(2)

已经被国内外许多作者进行了深入研究, 并且得到许多重要结果[1-11], 其中Ω是RN中的区域,V(·):Ω→R,f∈C(Ω×R,R),a,b>0是常数. 许多作者研究了Kirchhoff方程的基态解、正解、多重解等问题. 文献[5]用Nehair流形及紧性原理证明了问题(2)基态解的存在性. 其他有关Kirchhoff方程的研究可参看文献[12-16].然而,研究Kirchhoff方程变号解的结果还不多,文献[17]研究了三维情形下Kirchhoff方程变号解的存在性,他们的非线性项都是次临界增长,也就是|f(x,t)|≤C(1+|t|p),p∈(1,5).受此启发, 本文研究带有指数增长的Kirchhoff方程变号解的存在性.

(u,v)=∫Ω▽u·▽v,‖u‖=(u,u)1/2.

空间Lp(Ω)是通常的Lebesgue空间, 其范数记为|·|p, 1≤p<∞.C和Ck代表不同的正常数.u+(x)=max{0,u(x)},u-(x)=min{0,u(x)}.R+:=[0,+∞).

问题(1)对应的能量泛函为

显然I∈C1(X,R), 且∀u,v∈X,

〈I′(u),v〉=a∫Ω▽u·▽v+b∫Ω|▽u|2∫Ω▽u·▽v-∫Ωf(u)v.

定义M={u∈X:u±≠0,〈I′(u),u+〉=〈I′(u),u-〉=0}.m=min{I(u):u∈M}.

定理1假设 (f1)～(f4)成立,那么方程(1)有一个最小能量变号解.

1预备知识

引理1假设f满足(f1)～(f4),则对每个u≠0,u∈X,有

证明(ⅰ) 由(f1)，(f2)知,∀β,ε>0,固定的p≥1,都存在Cβ,ε,p，使得

|f(t)|≤ε|t|+Cβ,ε,p|t|p-1exp(βt2),t∈R,

(3)

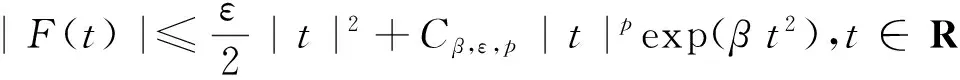
(4)

由文献[18],存在常数C只与Ω有关, 使得当u∈X{0},α‖u‖2≤4π时,

∫Ωexp(α|u(x)|2)dx=∫Ωexp(α‖u‖2)[u(x)/‖u‖2]dx≤C.

(5)

取β‖u‖2≤2π,p>2.由式(3)及(5)知,

(6)

由式(6)知

故由ε的任意性及p>2可得

(ⅱ) 由(f2)～(f4)易知,∀M>0,∃C>0,使得

f(t)t≥Mt4-Ct2,t∈R.

故可得

f(tu)tu≥Mt4u4-Ct2u2,t∈R.

上式同除t4并积分后取极限得

由M的任意性可得

(ⅲ)与(ⅱ)的证明类似.

引理2[19]假设f满足条件(f1)～(f4), 序列 {un}⊂X,使得un⇀u,则

∫Ωf(un)un→∫Ωf(u)u,∫ΩF(un)→∫ΩF(u).

类似于文献[17]有下面几个引理, 但值得注意的是引理3的证明不同于文献[16],本文用Brouwer不动点定理证明M的非空性.

引理3假设(f1)～(f4)成立, 则∀u∈X,u±≠0, 存在唯一正数对(su,tu), 使得suu++tuu-∈M.

证明对给定的u∈X,u±≠0, 定义泛函Φu(s,t)=I(su++tu-),(s,t)∈R+×R+. 直接计算可得

事实上, 由Φu的定义知

(7)

即

(8)

下面用Brouwer不动点定理证明Φu存在临界点.由φ1,φ2的性质知存在C1>0, 使得φ1(t)≤t,t>C1;φ2(s)≤s,s>C1. 令C2=max{maxt∈[0,C1]φ1(t),maxs∈[0,C1]φ2(s)},C=max{C1,C2}.定义H:[0,C]×[0,C]→R+×R+,H(s,t)=(φ1(t),φ2(s)).由定义可知H(s,t)∈[0,C]×[0,C].注意到H是连续的,故由Brouwer不动点定理知∃(s′,t′)∈[0,C]×[0,C], 使得(φ1(t′),φ2(s′))=(s′,t′). 通过φ1,φ2的定义知

因此, (s′,t′)是Φu的临界点. 下证临界点是唯一的.

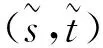
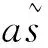
(9)

(10)

由式(9)知

(11)

引理4[13]假设u∈X,u±≠0, 则(su,tu)是Φu(s,t)的唯一的最大值点, 其中(su,tu)由引理3得到.

引理5[13]假设(f1)～(f4)成立,且u∈X,u±≠0, 〈I′(u),u+〉≤0, 〈I′(u),u-〉≤0, 则0

引理6[13]假设(f1)～(f4)成立,则m>0可达,即∃u∈M,使得m=I(u).

2定理1的证明

证明证明引理6得到的极小化点u就是问题(1)的变号解. 用形变引理证明I′(u)=0.

令λ=min{|u+|2,|u-|2},由嵌入定理知|u|2≤S‖u‖,其中S为嵌入常数.

反证法. 假设I′(u)≠0,则∃r>0,α>0,使得‖v-u‖≤r时,‖I′(v)‖≥α.

‖I′(v)‖≥8ε/δ,v∈I-1([m-2ε,m+2ε])∩S2δ.

(12)

应用形变引理[20],则存在泛函η∈([0,1]×X,X),使得

(a)u∉I-1([m-2ε,m+2ε])∩S2δ时,η(1,u)=u.

(b)η(1,Im+ε∩S)⊂Im-ε.

(c) ‖η(1,u)-u‖≤δ,u∈X.

首先证明

(13)

由引理4知,I(φ(s,t)))≤m

下证

η(1,φ(D))∩M≠∅.

定义γ(s,t):=η(1,φ(s,t)),

Ψ1(s,t)=(〈I′(φ(s,t)),su+〉),〈I′(φ(s,t)),su-〉)=(P(s,t),Q(s,t)),

Ψ2(s,t)=(〈I(γ(s,t)),(γ(s,t))+〉,〈I(γ(s,t)),(γ(s,t))-〉).

直接计算得

因为Ψ1是C1的且(1,1)是一个孤立零点,故

deg(ψ1,D,0)=ind(ψ1,(1,1))=sgnJΨ1(1,1)=1.

参考文献(References):

[1]HEXiaoming,ZOUWenming.InfinitelymanypositivesolutionsforKirchhoff-typeproblems[J].NonlinearAnal,2009,70(3):1407-1414.

[2]HEXiaoming,ZOUWenming.ExistenceandconcentrationbehaviorofpositivesolutionsforaKirchhhoffequationinR3[J].JDifferentialEquations,2012,252(2):1813-1834.

[3]LIGongbao,YEHongyu.ExistenceofpositivegroundstatesolutionsforthenonlinearKirchhofftypeequationsinR3[J].JDifferentialEquations,2014,257(2):566-600.

[4]MAOAnmin,ZHANGZhitao.Sign-changingandmultiplesolutionsofKirchhofftypeproblemswithouttheP.S.condition[J].NonlinearAnal,2009,70(3):1275-1287.

[5]ZHANGHui,ZHANGFubao.GroundstatesforthenonlinearKirchhofftypeproblems[J].JMathAnalAppl,2015,423(2):1671-1692.

[6]WANGZhengping，ZHOUHuansong.Sign-changingsolutionsforthenonlinearSchödinger-PoissonsysteminR3[J].CalcVarPDEs，2015，52(3):927-943.

[7]GUOZ.GroundstatesforKirchhoffequationswithoutcompactcondition[J].JDifferentialEquations,2015,259(7):2884-2902.

[8]LIUZhisu,GUOShuanjiang.ExistenceofpositivegroundstatesolutionsforKirchhofftypeproblems[J].NonlinearAnal,2015,120:1-13.

[9]ZHANGZhitao,PERERAK.SignchangingsolutionsofKirchhofftypeproblemsviainvariantsetsofdescentflow[J].JMathAppl,2006,317(2):456-463.

[10]XIEQilin,MAShiwang.ExistenceandconcentrationofpositivesolutionsforKirchhoff-typeproblemswithasteepwellpotential[J].JMathAnalAppl,2015,431(2):1210-1223.

[11]李宝平.一类Kirchhoff方程解的存在性与渐进性质[J].数学的实践与认识，2015,45(19)：265-270.

LIBaoping.ExistenceandasymptoticbehaviorofthesolutionforaclassofKirchhoffequation[J].MathematicsinPracticeandTheory,2015,45(19)：265-270.

[12]王田娥，李健，李俊杰，等.一类超线性p-Kirchhoff型方程非平凡解的存在性[J].吉林大学学报：理学版，2015,53(2)：161-165.

WANGTian′e,LIJian,LIJunjie,etal.Existenceofnontrivialsolutionsofaclassofp-Kirchhofftypeequations[J].JournalofJilinUniversity:ScienceEdition,2015,53(2)：161-165.

[13]廖家锋,张鹏,唐春雷.一类渐近4次线性Kirchhoff方程的多解性[J].西南师范大学学报:自然科学版,2014,39(8):8-11.

LIAOJiafeng,ZHANGPeng,TANGChunlei.Onmultiplicityofsolutionsforaclassofasymptotically4-linearKirchhoffequations[J].JournalofSouthwestChinaNormalUniversity:NaturalScienceEdition,2014,39(8):8-11.

[14]宋宇鹏.一类p-Kirchhoff方程无穷多解的存在性[J].纺织高校基础科学学报,2015,28(2):204-207.

SONGYupeng.Existenceofinfinitelymanysolutionsforaclassofp-Kirchhoffequations[J].BasicSciencesJournalofTextileUniversities,2015,28(2):204-207.

[15]王瑞娜，王小军，高小丽.Kirchhoff方程解的存在性与多解性[J].太原师范学院学报：自然科学版，2011，10(4):4-7.

WANGRuina,WANGXiaojun,GAOXiaoli.ExistenceandmultiplicityofsolutionstoKirchhofftypeequations[J].JournalofTaiyuanNormalUniversity:NaturalScienceEdition,2011,10(4):4-7.

[16]姜静香.一类Kirchhoff型方程退化时整体解的存在性[J].渤海大学学报：自然科学版，2015，36(1):10-15.

JIANGJingxiang.ExistenceofglobalsolutionsoftheequationsofdegenerateKirchhofftype[J].JournalofBohaiUniversity:NaturalScienceEdition,2015,36(1):10-15.

[17]WEIShuai.Sign-changingsolutionsforaclassofKirchhoff-typeprobleminboundeddomains[J].JDifferentialEquations,2015,259(4):1256-1274.

[18]MOSERJ.AsharpformofaninequalitybyN.Trudinger[J].JIndianaUnivMath,1970,20(11):1077-1092.

[19]FIGUEIREDODGD,MIYAGAKIOH,RUFB.EllipticequationsinR2withnonlinearitiesinthecriticalgrowthrange[J].CalcVarPartialDifferentialEquations,1995,3(2):139-153.

[20]WILLEMM.Minimaxtheorems[M].Boston:Birkhauser,1996:24.

编辑、校对：师琅

文章编号:1006-8341(2016)02-0135-06

DOI：10.13338/j.issn.1006-8341.2016.02.001

收稿日期：2015-08-31

基金项目:国家自然科学基金资助项目(11571209，11301313)；山西省自然科学基金资助项目(2014021009-1,2015021007)

作者简介:郭红(1991—)，女，山西省大同市人，山西大学硕士研究生，研究方向为非线性泛函.E-mail:18835126525@163.com

中图分类号：O 175.25; O 177

文献标识码：A

Existence of sign-changing solution with least energy for a class of Kirchhoff equations

GUOHong

(School of Mathematic and Science,Shanxi University,Taiyuan 030006,China)

Abstract:The existence of sign-changing solution with least energy for a Kirchhoff equation is studied, where the nonlinearity satisfies an exponential growth.Firstly, Brouwer fixed point theorem is used to prove M is nonempty. Secondly, the minimizer of the energy functional on M is found. Then the minimizer is a sign-changing solution with least energy of the Kirchhoff equation is proved by quantitative deformation lemma. Because the appearance of nonlocal term,the usual variational approach is not applicable,so the energy function is restricted on M, a sign-changing solution with least energy for a Kirchhoff equation is obtained.

Key words:Kirchhoff equation; Brouwer fixed point;quantitative lemma;sign-changing solution; least energy

引文格式：郭红.一类Kirchhoff方程最小能量变号解的存在性[J].纺织高校基础科学学报,2016,29(2)：135-140.

GUO Hong.Existence of sign-changing solution with least energy for a class of Kirchhoff equations[J].Basic Sciences Journal of Textile Universities,2016,29(2):135-140.