有关对称无权图生成树数目的拆分定理

龚和林，王　伟

(1.厦门大学数学科学学院,福建厦门361005；2.塔里木大学信息工程学院,新疆阿拉尔843300)



有关对称无权图生成树数目的拆分定理

龚和林1*，王伟1，2

(1.厦门大学数学科学学院,福建厦门361005；2.塔里木大学信息工程学院,新疆阿拉尔843300)

摘要：设G是一个对称平面图.Ciucu等证明了一个有关G的生成树数目的拆分定理,也就是G的生成树数目可用两个小图的生成树数目乘积来表示.在此基础上，提出了一种图变换,给出了图在这种变换下生成树数目的变化关系式,再结合矩阵-树定理给出了该拆分定理的一个简短证明.同时,受 Zhang等证明的赋权图生成树权和的拆分定理启发,还给出了一个关于对称无权图生成树数目的等价拆分公式.

关键词：生成树数目;矩阵-树定理;对称性;平面图

给定图G=(V(G),E(G)).若v∈V(G),记dG(v)为v在G中的度.若U⊆V(G),记G[U]为U的导出子图.在顶点标号下,连通无权图G的不同生成树的个数记为t(G).其他图论术语及符号参考文献[1-2].

对平面图G,称G是反射对称,如果存在某直线l(对称轴)使G在关于l反射作用下分为互为镜像的两个部分.有关反射对称平面图的结果,可参见文献[3-6].设G是一个关于轴l反射对称的平面图,且G存在一个顶点划分{VL,VC,VR},满足V(G)=VL∪VC∪VR,{VL,VC,VR}两两不交,这里,VC={v1,v2,…,vn}在轴l上,VL和VR在轴l的左右两侧,且VL和VR之间不存在跨过l的边.记GL=G[VL∪VC],GR=G[VC∪VR],GC=G[VC],则GL≅GR(同构).定义G1为在图GL基础对子图GC的每条边插入一个新顶点(边剖分运算)后得到的图,G2为在图GR基础上对VC中顶点黏合成一个顶点u后得到的图(删去产生的自环,可能产生重边).Ciucu等[4]证明了

t(G)=2ω(G)t(G1)t(G2)，

(1)

这里,ω(G)为G中交于对称轴l的有界面的个数,见文献[4]示例图2(a).

定义1[7]称连通图G具有对合性质的,也说G是左右对称的,如果G满足下列条件:

(i)V(G)=VL∪VC∪VR,这里,VL,VC,VR非空且两两不交,VL,VR在VC的左右两侧.

(ii) 记GL=G[VL∪VC],GR=G[VC∪VR],GC=G[VC].则E(G)=E(GL)∪E(GC)∪E(GR)∪E(VL,VR),这里,E(VL,VR)为连接VL与VR中顶点的边集合.

(iii) 如果VL={x1,x2,…,xs},VR={y1,y2,…,ys},VC={v1,v2,…,vn},那么G存在一个自同构映射f,使得f(xi)=yi,f(yi)=xi(i∈{1,2,…,s}),f(v)=v(v∈VC).这样的映射f称为G的对合映射.也就是说,f∈Aut(G)(G的自同构群),且f≠id(恒同映射),但f2=id.

对左右对称图G,记G1为在图GL基础上对子图GC的每条边插入一新顶点(边剖分运算)后得到的图,当E(GC)=ø,规定G1=GL;G2为在图GR基础上将VC中顶点黏合成一个顶点u后得到的图(删去产生的自环).对左右对称图G,在满足条件E(VL,VR)⊆{xiyi∈E(G)，i=1,2,…,s}下,假设|VC|=n≥1,|E(GC)|=m≥0,且G3是由G2添加一些平行边得到的图:只要ei=xiyi∈E(VL,VR),就在G2上用一对平行边连接u与yi.在本文中将证明

t(G)=2n-m-1t(G1)t(G3).

(2)

特别地,当E(VL,VR)=ø 时,G3=G2,因此,式(2) 即为

t(G)=2n-m-1t(G1)t(G2).

(3)

下面将说明式(3)可直接推出式(1).

给定一个赋权图 G,用 ω(e) 表示 e 的权,T(G) 表示G的基础无权图所有生成树组成的集合.若T∈T(G),则T的权记为W(T)=∏e∈E(T)ω(e)，进一步,G的生成树权和定义为τ(G)=∑T∈T(G)W(T).特别地,赋权图G具有对合映射f,意味着f保持权不变,即 ∀e∈E(G),ω(e)=ω(f(e)).

在上述权和的定义和特定赋权下,Zhang等[7]证明了下面定理.

定理1[7]设G是一个具有对合映射 f 的赋权图.若 |VC|=n≥1,则

(4)

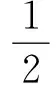
(ii) 若 xiyj,xjyi(i≠j.对合映射 f 保证这两条边必须成对出现,且它们权一样,记为 α) 是 G 的一对交错边,则 xi和 xj增加一条边 xixj(允许重边),并赋权 α.

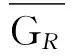
(i) 在 GR基础上将顶点子集 VC顶点黏合成一个顶点 u (去掉产生的环);

(ii) 只要边 xiyj∈E(VL,VR) (i 和 j 可相等或也可不等),且 ω(xiyj)=β,则增加边 uyj,并赋权 2β；

(iii) 若 xiyj,xjyi(i≠j.对合映射 f 保证这两条边必须成对出现,且它们权一样,记为 γ) 是 G 的一对交错边,则 yi和 yj增加一条边 yiyj(允许重边),并赋负权-γ.

1几个预备引理

设G是一个图,e是G的一条非环边且u和v为e的两个端点.记G-e为图G删去边e后得到的子图,G/e为图G的收缩边e后得到的图.此外,从G到Ge的变换过程称为G的关于e的双剖分变换,这里Ge是在图G的基础上把边e替换为两条内不交的长为 2 的路得到的图，如图1表示.

图1　边e的双剖分变换Fig.1Double subdivision on the edge e

引理1设G是一个连通图,Ge是在G基础上对非环边e作双剖分变换得到的图，则t(Ge)=4t(G).

证明因为Ge中边导出子图G[e1,e2,e3,e4] 恰有 4 棵不同的生成树,也恰有 4 棵含 2 个分支的生成森林 (u和v在不同的连通分支),所以G的 1 棵(含或不含e) 的生成树可构造Ge的 4 棵不同生成树.

引理2[1,8](矩阵-树定理) 设G是一个连通图，记L(G)=D(G)-A(G),其中,D(G)为G 的度矩阵,A(G) 为 G 的邻接矩阵，则t(G)=det(Li(G)).这里,Li(G) 为 L(G) 删去第 i 行第 i 列所得的子矩阵.

引理3是文献[7]中定理 2.1 的特例,区别于文献[9] 中的图谱方法[9],用矩阵-树定理给出一种简洁证明.

引理3[7]如果 G=(V(G),E(G)) 是左右对称图,且 |VC|=n≥1,E(GC)=E(VL,VR)=ø,那么

t(G)=2n-1t(G1)t(G2)=

2n-1t(GL)t(G2)(G1=GL).

证明用AL(或AR) 表示G[VL] (或G[VR]) 的邻接矩阵,B表示 VL和 VC的关联矩阵,DL(或DR) 分别为以 dG(x1),dG(x2),…,dG(xs) (或 dG(y1),dG(y2),…,dG(ys)) 为对角元素的对角矩阵,DC为以 VC中顶点度 dG(v1),dG(v2),…,dG(vn) 为对角元素的对角矩阵.容易看出,

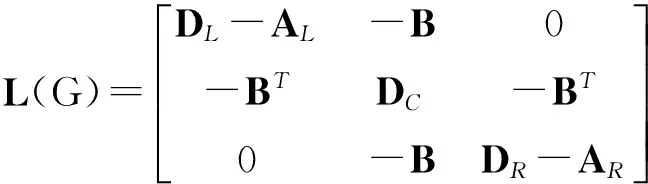
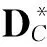
Lv(G)=

(DL=DR,AL=AR).

注意到

t(G1)=det(Lu(G1))=

其中,u 是 G2中由 VC中顶点黏和得到的新顶点,du是 u 在 G2中的度,且 u 与 VR的邻接关系为向量X∈R1×|VR|.显然,t(G2)=det(Lu(G2))=det(DR-AR).因此,

t(G)=det(Lv(G))=

2n-1det(Lv(G1))det(Lu(G2))=

2n-1t(G1)t(G2).

2对称无权图生成树数目的两个拆分定理

对具有对合性质的赋权图,Zhang等[4]给出了一个有关生成树权和的拆分定理.受之启发,下面将证明公式 (2) (见定理 3).为清晰起见,逐步归纳证明,尽管定理 3 蕴含定理 2.

定理2设G 是一个左右对称图.若 |VC|=n≥1,|E(GC)|=m≥0,E(VL,VR)=ø，则

t(G)=2n-m-1t(G1)t(G2).

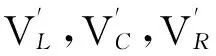
2n-k-3t((Ge)1)t((Ge)2)=

2n-(k+1)-1t(G1)t(G2).

推论1[9]设 G 是一个关于轴 l 反射对称平面图,且 ω(G) 为 G 中交于轴的有界面的个数.若 |VC|=n≥1,E(VL,VR)=ø，则 t(G)=2ω(G)t(G1)t(G2).

证明不失一般性,不妨设 v1,v2,…,vn自上而下排列在轴 l 上,且边集 E(GC)⊆{vivi+1，i=1,2,…,n-1}(既然 G 是反射对称的平面图,合理排序 VC上的顶点可满足要求).注意到 n-1-|E(GC)|=n-1-m=ω(G).因此,根据定理 2 得 t(G)=2ω(G)t(G1)t(G2).

定理3设 G 是一个左右对称图.若 |VC|=n≥1,|E(GC)|=m≥0,且 E(VL,VR)={e1,e2,…,ek}⊆{xiyi∈E(G)，i=1,2,…,s} (无交错边对),则

t(G)=2n-m-1t(G1)t(G3).

这里,G3由 G2添加一些平行边得到:只要 ei=xiyi∈E(VL,VR),就在 G2上用一对平行边连接 u 与 yi.

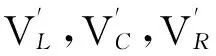
参考文献：

[1]BIGGSNL.Algebraicgraphtheory[M].2nded.Cambridge:CambridgeUniversityPress,1993:9-33.

[2]BONDYJA,MURTYUSR.Graphtheorywithapplications[M].NewYork:Elsevier,1976:7,218-219.

[3]CIUCUM.Enumerationofperfectmatchingsingraphswithreflectivesymmetry[J].JCombinTheorySerA,1997,77:67-97.

[4]CIUCUM,YANW,ZHANGF.Thenumberofspanningtreesofplanegraphswithreflectivesymmetry[J].JCombinTheorySerA,2005,112:105-116.

[5]JINX,ZHANGF.Alexanderpolynomialforevengraphswithreflectivesymmetry[J].JKnotTheorRamif,2008,17:1241-1256.

[6]NEGAMIS.Polynomialinvariantofgraphs[J].TranAmerMathSoc,1987,209:601-622.

[7]ZHANGF,YANW.Enumerationofspanningtreesofgraphswithaninvolution[J].JCombinTheorySerA,2009,116:650-662.

[8]KIRCHHOFFG.Überdieauflösungdergleichungen,aufwelchemanbeideruntersuchungderlinearenverteilunggalvanischerströmegeführtwird[J].AnnPhysChem,1847,72:497-508.

doi：10.6043/j.issn.0438-0479.201512026

收稿日期：2015-12-27录用日期：2016-05-05

基金项目：国家自然科学基金(11271307,11561058)；广西高校数学与统计模型重点实验室开放课题

*通信作者：helingong@126.com

中图分类号:O 157.5

文献标志码：A

文章编号：0438-0479(2016)04-0554-04

The Factorization Theorems on the Number of Spanning Trees of Graphs with Some Symmetry

GONG Helin1*,WANG Wei1，2

(1.School of Mathematical Sciences,Xiamen University,Xiamen 361005，China；2.College of Information Engineering,Tarim University,Alar 843300，China)

Abstract:Let G be a plane graph with reflective symmetry.Ciucu,et al, proved a factorization theorem on the number of spanning trees of G.That is,the number of spanning treesof G can be expressed in terms of the product of the number of spanning trees of two smaller graphs.In this paper,we introduce a graph transformation and discuss its effect on the number of spanning trees,then by the matrix-tree theorem we give a short proof of above-mentioned factorization theorem.Motivated by a factorization theorem on the sum of weights of spanning trees of weighted graphs with some symmetry in Zhang et al,we further provide an equivalent factorization formula on the number of spanning trees of unweighted graphs with some symmetry.

Key words:spanning trees number;matrix-tree theorem;symmetry;plane graph

引文格式：龚和林，王伟.有关对称无权图生成树数目的拆分定理[J].厦门大学学报(自然科学版)，2016,55(4)：554-557.

Citation：GONG H L,WANG W．The factorization theorems on the number of spanning trees of graphs with some symmetry[J].Journal of Xiamen University(Natural Science)，2016,55(4)：554-557．(in Chinese)