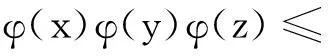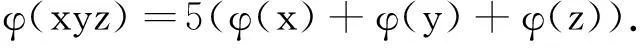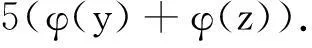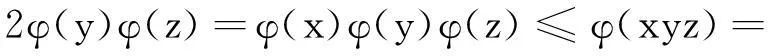不定方程φ(xyz)=5(φ(x)+φ(y)+φ(z))的正整数解

官春梅，吴星星，张四保，席小忠

(1.喀什大学数学与统计学院，新疆喀什　844008；2.新疆大学数学与系统科学学院，新疆乌鲁木齐　830046；3.宜春学院数学与计算机科学学院,江西宜春　336000)



不定方程φ(xyz)=5(φ(x)+φ(y)+φ(z))的正整数解

官春梅1，吴星星2，张四保1，席小忠3

(1.喀什大学数学与统计学院，新疆喀什844008；2.新疆大学数学与系统科学学院，新疆乌鲁木齐830046；3.宜春学院数学与计算机科学学院,江西宜春336000)

讨论了不定方程φ(xyz)=5(φ(x)+φ(y)+φ(z))的可解性，利用初等方法给出了该方程的57组正整数解，其中φ(n)为Euler函数.

Euler函数；不定方程；正整数解；初等方法

0　引言

记φ(n)为Euler函数，其值等于模n的一个完全剩余系中与n互素的整数的个数.有关Euler函数φ(n)的方程的研究是初等数论中非常重要和有意义的课题之一[1].求方程φ(x)=m的所有正整数解是有关Euler函数研究的一个公开问题．Erdös[2]与Woolridge[3]都曾研究过这一问题，并给出了相应的成果．文献[4]讨论了方程φ(x1+x2+…+xk)=φ(x1)+φ(x2)+…+φ(xk)的可解性，并给出其所有的整数解；文献[5]讨论了φ(xyz)=2(φ(x)+φ(y)+φ(z))的可解性问题，并给出了其全部正整数解.本文讨论方程φ(xyz)=5(φ(x)+φ(y)+φ(z))的可解性问题，并利用初等方法给出其全部正整数解.

1　主要引理

引理1[6]对任意正整数n与m，有

其中gcd(n,m)为n与m的最大公因数.

引理2[6]若整数n≥2，则φ(n)

2　结论及其证明

定理1不定方程

(1)

有57组正整数解：

(x,y,z)=(25,3,3)，(44,3,3)，(50,3,3)，(33,3,4)，(33,4,3)，(25,3,6)，(25,6,3)，(11,3,5)，(22,3,5)，(11,3,10)，(11,3,8)，(11,4,5)，(11,6,5)，(11,5,3)，(22,5,3)，(11,10,3)，(11,8,3)，(11,5,4)，(11,5,6)，(3,3,25)，(3,3,44)，(3,3,50)，(3,4,33)，(3,6,25)，(4,3,33)，(6,3,25)，(3,25,3)，(3,44,3)，(3,50,3)，(3,33,4)，(3,25,6)，(4,33,3)，(6,25,3)，(3,5,11)，(3,11,5)，(3,5,22)，(3,22,5)，(3,8,11)，(3,11,8)，(3,10,11)，(3,11,10)，(4,5,11)，(4,11,5)，(6,5,11)，(6,11,5)，(5,3,11)，(5,11,3)，(5,3,22)，(5,22,3)，(8,3,11)，(8,11,3)，(10,3,11)，(10,11,3)，(5,4,11)，(5,11,4)，(5,6,11)，(5,11,6).

证明由于φ(xyz)=5(φ(x)+φ(y)+φ(z))，所以

从而有φ(x)φ(y)φ(z)≤5(φ(x)+φ(y)+φ(z))，即

下面根据φ(y)φ(z)的值分以下两种情况进行讨论.

情况1φ(y)φ(z)<5.

当φ(y)φ(z)<5时，(y,z)的可能取值为：(y,z)=(1,1)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(1,8)，(1,10)，(1,12)，(2,1)，(2,2)，(2,3)，(2,4)，(2,5)，(2,6)，(2,8)，(2,10)，(2,12)，(3,1)，(3,2)，(3,3)，(3,4)，(3,6)，(4,1)，(4,2)，(4,3)，(4,4)，(4,6)，(5,1)，(5,2)，(6,1)，(6,2)，(6,3)，(6,4)，(6,6)，(8,1)，(8,2)，(10,1)，(10,2)，(12,1)，(12,2).

将以上(y,z)的值代入方程(1)，结合引理1与引理2可得，当(y,z)=(3,3)时，方程(1)有正整数解(x,y,z)=(25,3,3)，(44,3,3)，(50,3,3)；当(y,z)=(3,4)时，方程(1)有正整数解(x,y,z)=(33,3,4)；当(y,z)=(4,3)时，方程(1)有正整数解(x,y,z)=(33,4,3)；当(y,z)=(3,6)时，方程(1)有正整数解(x,y,z)=(25,3,6)；当(y,z)=(6,3)时，方程(1)有正整数解(x,y,z)=(25,6,3).在其余情况下方程(1)均无正整数解.

情况2φ(y)φ(z)>5.

此时，必有φ(y)φ(z)≥6.

情况2.1φ(y)φ(z)=6.

此时，有φ(y)=1，φ(z)=6或φ(y)=6，φ(z)=1.从而φ(xyz)=5φ(x)+35，即φ(xyz)-5φ(x)=35，由此所确定的(y,z)都不会使得φ(x)为偶数，由引理2可得此时方程(1)无正整数解.

情况2.2φ(y)φ(z)=8.

此时，有φ(y)=1,φ(z)=8或φ(y)=2,φ(z)=4或φ(y)=4,φ(z)=2或φ(y)=8,φ(z)=1.

当φ(y)=1,φ(z)=8或φ(y)=8,φ(z)=1时，有φ(xyz)=5φ(x)+45，从而有φ(xyz)-5φ(x)=45，由此所确定的(y,z)都不会使得φ(x)为偶数，由引理2可得此时方程(1)无正整数解.

当φ(y)=2,φ(z)=4时，有y=3,4,6且z=5,10,8,12.此时，(y,z)的可能取值为：(y,z)=(3,5)，(3,10)，(3,8)，(3,12)，(4,5)，(4,10)，(4,8)，(4,12)，(6,5)，(6,10)，(6,8)，(6,12).

当(y,z)=(3,5)时，方程(1)有正整数解(x,y,z)=(11,3,5)，(22,3,5)；当(y,z)=(3,10)时，方程(1)有正整数解(x,y,z)=(11,3,10)；当(y,z)=(3,8)时，方程(1)有正整数解(x,y,z)=(11,3,8)；当(y,z)=(4,5)时，方程(1)有正整数解(x,y,z)=(11,4,5)；当(y,z)=(6,5)时，方程(1)有正整数解(x,y,z)=(11,6,5)；而当(y,z)=(3,12)，(4,10)，(4,8)，(4,12)，(6,10)，(6,8)，(6,12)时，方程(1)均无正整数解.

由此可知，当φ(y)=4,φ(z)=2时，方程(1)有正整数解(x,y,z)=(11,5,3)，(22,5,3)，(11,10,3)，(11,8,3)，(11,5,4)，(11,5,6).

综上，当φ(y)φ(z)=8时，方程(1)有正整数解(x,y,z)=(11,3,5)，(22,3,5)，(11,3,10)，(11,3,8)，(11,4,5)，(11,6,5)，(11,5,3)，(22,5,3)，(11,10,3)，(11,8,3)，(11,5,4)，(11,5,6).

情况2.3φ(y)φ(z)=10.

此时，有φ(y)=1,φ(z)=10或φ(y)=10,φ(z)=1.从而有5(φ(y)+φ(z))=55，即φ(xyz)-5φ(x)=55，可得φ(x)的值为奇数或者无正整数解.因而，当φ(y)φ(z)=10时方程(1)无正整数解.

情况2.4φ(y)φ(z)=12.

此时，有φ(y)=1,φ(z)=12或φ(y)=2,φ(z)=6或φ(y)=6,φ(z)=2或φ(y)=12,φ(z)=1.

当φ(y)=1,φ(z)=12或φ(y)=12,φ(z)=1时，有5(φ(y)+φ(z))=65，从而φ(xyz)-5φ(x)=65，可得φ(x)的值为奇数或者无正整数解.因而，此时方程(1)无正整数解.

当φ(y)=2,φ(z)=6时，有y=3,4,6且z=7,9,14,18.此时，(y,z)的可能取值为：(y,z)=(3,7)，(3,9)，(3,14)，(3,18)，(4,7)，(4,9)，(4,14)，(4,18)，(6,7)，(6,9)，(6,14)，(6,18).将以上每组值代入方程(1)可得，此时方程(1)无正整数解.同理，当φ(y)=6,φ(z)=2时，方程(1)无正整数解.

综合以上讨论，当φ(y)φ(z)=12时，方程(1)无正整数解.

情况2.5φ(y)φ(z)=14.

此时，有φ(y)=14或者φ(z)=14.由于方程φ(m)=14无正整数解，因而，此时方程(1)无正整数解.

情况2.6φ(y)φ(z)=16.

此时，有φ(y)=1,φ(z)=16或φ(y)=2,φ(z)=8或φ(y)=4,φ(z)=4或φ(y)=8,φ(z)=2或φ(y)=16,φ(z)=1.

当φ(y)=1,φ(z)=16或φ(y)=16,φ(z)=1时，有5(φ(y)+φ(z))=85，从而φ(16x)-5φ(x)=85，可得φ(x)的值为奇数或者无正整数解.因而，此时方程(1)无正整数解.

当φ(y)=2,φ(z)=8时，有y=3,4,6且z=15,30,20,16,24.此时，(y,z)的可能取值为:(y,z)=(3,15)，(3,30)，(3,20)，(3,16)，(3,24)，(4,15)，(4,30)，(4,20)，(4,16)，(4,24)，(6,15)，(6,30)，(6,20)，(6,16)，(6,24).将以上各组数值代入方程(1)可得此时方程(1)无正整数解.

当φ(y)=4,φ(z)=4时，有y=5,8,10,12且z=5,8,10,12.此时，(y,z)的可能取值为：(y,z)=(5,5)，(5,8)，(5,10)，(5,12)，(8,5)，(8,8)，(8,10)，(8,12)，(10,5)，(10,8)，(10,10)，(10,12)，(12,5)，(12,8)，(12,10)，(12,12).同样地，将以上各组数值代入方程(1)可得此时方程(1)无正整数解.

综合以上讨论，当φ(y)φ(z)=16时方程(1)无正整数解.

情况2.7φ(y)φ(z)=18.

此时，有φ(y)=1,φ(z)=18或φ(y)=18,φ(z)=1，从而有5(φ(y)+φ(z))=95，即φ(xyz)-5φ(x)=95，可得φ(x)的值为奇数或者无正整数解.因而，此时方程(1)无正整数解.

情况2.8当φ(y)φ(z)≥20时，由于φ(y)，φ(z)均为正整数，所以(φ(y)-1)(φ(z)-1)≥0，即φ(y)φ(z)+1≥φ(y)+φ(z).由方程(1)有

所以，φ(x)=1，2，4，6.

情况2.8.1φ(x)=1.

此时，由方程(1)可得

于是有(φ(y)-5)(φ(z)-5)≤30.

当(φ(y)-5)(φ(z)-5)<0时，若φ(y)=1,2,4，则φ(z)≥6.此时，有φ(x)=1,φ(y)=1或φ(x)=1,φ(y)=2或φ(x)=1,φ(y)=4.根据情况1关于φ(y)φ(z)<6的讨论可知，此时方程(1)无正整数解.同理，当φ(z)=1,2,4，φ(y)≥6时，方程(1)无正整数解.

当(φ(y)-5)(φ(z)-5)≥0时，此时有(φ(y)-5)(φ(z)-5)=0,1,2,…,30.

当(φ(y)-5)(φ(z)-5)=0时，φ(y)，φ(z)至少有一个等于5，但这都不可能成立；当(φ(y)-5)(φ(z)-5)=k(k为偶数)时，φ(y)-5与φ(z)-5中至少有一个为偶数，从而φ(y)，φ(z)中至少有一个为奇数，因而此时方程(1)无正整数解.从而只需讨论当(φ(y)-5)(φ(z)-5)=1，3，5，7，9，11，13，15，17，19，21，23，25，27，29的情况.由于当(φ(y)-5)(φ(z)-5)=1，3，5，7，9，11，13，15，17，19，21，23，25，27，29时，所有的φ(y)与φ(z)都是偶数，而φ(x)=1，所以5(φ(x)+φ(y)+ φ(z))为一个至少大于35的奇数，由引理2可得，此时方程(1)无正整数解.

情况2.8.2φ(x) =2.

此时，由方程(1)可得

于是有(φ(y)-3)(φ(z)-3)<15.

当(φ(y)-3)(φ(z)-3)<0时，若φ(y)=1，则φ(z)≥4且为偶数，结合φ(x)=2有5(φ(x)+φ(y)+φ(z))为一个至少大于25的奇数，由引理2可得，此时方程(1)无正整数解.同理，当φ(z)=1，φ(y)≥4时，方程(1)无正整数解.若φ(y)=2，结合φ(x)=2，有x=y=3,4,6，由此可得(x,y)的所有可能值：(x,y)=(3,3)，(3,4)，(3,6)，(4,3)，(4,4)，(4,6)，(6,3)，(6,4)，(6,6).经计算，此时方程(1)有正整数解(x,y,z)=(3,3,25)，(3,3,44)，(3,3,50)，(3,4,33)，(3,6,25)，(4,3,33)，(6,3,25).同理，当φ(z)=2，φ(x)=2时，方程(1)有正整数解(x,y,z)=(3,25,3)，(3,44,3)，(3,50,3)，(3,33,4)，(3,25,6)，(4,33,3)，(6,25,3).

当(φ(y)-3)(φ(z) -3)=0,2,4,6,8,10,12,14时，φ(y)与φ(z)中至少有一个为奇数，因而此时方程(1)无正整数解，那么只需讨论(φ(y)-3)(φ(z)-3)=1,3,5,7,9,11,13这7种情况.

当(φ(y)-3)(φ(z)-3)=1,3,5,7,9,13时，φ(y)与φ(z)中至少有一个满足φ(m)=4，结合φ(x)=2，只需讨论φ(x)=2,φ(m)=4的情况来确定方程(1)的正整数解的情况，其中m=y或者m=z.当φ(x)=2,φ(m)=4时，有x=3,4,6且m=5,8,10,12，因而(x,m)的所有可能取值有：(x,m)=(3,5)，(3,8)，(3,10)，(3,12)，(4,5)，(4,8)，(4,10)，(4,12)，(6,5)，(6,8)，(6,10)，(6,12)这12种情况.将以上(x,m)的值与φ(x)=2,φ(m)=4代入方程(1)可得，此时方程(1)在(φ(y)-3)(φ(z)-3)=7的情况下有正整数解(x,y,z)=(3,5,11)，(3,11,5)，(3,5,22)，(3,22,5)，(3,8,11)，(3,11,8)，(3,10,11)，(3,11,10)，(4,5,11)，(4,11,5)，(6,5,11)，(6,11,5)，而其余情况均无正整数解.

当(φ(y)-3)(φ(z)-3)=11时，有φ(y)=14或者φ(z)=14.由于φ(m)=14无正整数解，因而此时方程(1)无正整数解.

当(φ(y)-3)(φ(z)-3)=1时还有φ(y)=2,φ(z)=2这一情况，结合φ(x)=2，由情况1的讨论可得此时方程(1)无正整数解.

当(φ(y)-3)(φ(z)-3)=9时还有φ(y)=6,φ(z)=6这一情况，结合φ(x)=2，为了降低计算量，可由φ(x)=2,φ(y)=6来确定这一情形下方程(1)的正整数解，易得此时方程(1)无正整数解.

情况2.8.3φ(x)=4.

此时，由方程(1)可得

于是有(2φ(y)-3)(2φ(z)-3)<33.

当(2φ(y)-3)(2φ(z)-3)<0时，有φ(x)=1,φ(z)≥2或φ(y)≥2,φ(z)=1.根据情况1有关φ(y)φ(z)<5的讨论可知，此时方程(1)无正整数解.

当(2φ(y)-3)(2φ(z)-3)=1时，有φ(y)=1,φ(z)=1或φ(y)=2,φ(z)=2.对于这一情形，根据情况1中有关φ(y)φ(z)<5的讨论，结合φ(x)=4可知，此时方程(1)无正整数解.

当(2φ(y)-3)(2φ(z)-3)=2,3,4,6,7,8,10,11,12,14,15,16,18,19,20,22,23,24,26,27,28,30,31,32时，φ(y)与φ(z)中至少有一个为奇数或无正整数解，因而此时方程(1)无正整数解，那么只需讨论当(2φ(y)-3)(2φ(z)-3)=5,9,13,17,21,25,29时的情况.

当(2φ(y)-3)(2φ(z)-3)=5,9,13,17,21,29时，φ(y)与φ(z)中至少有一个满足φ(m)=2，结合φ(x)=4，通过考虑φ(x)=4,φ(m)=2来确定方程(1)的正整数解,其中m=y或者m=z.这正好与情况2.8.2中当(φ(y)-3)(φ(z)-3)=1,3,5,7,9,11,13的情况所确定φ(x)=2,φ(m)=4相对应，因而此时方程(1)有正整数解(x,y,z)=(5,3,11)，(5,11,3)，(5,3,22)，(5,22,3)，(8,3,11)，(8,11,3)，(10,3,11)，(10,11,3)，(5,4,11)，(5,11,4)，(5,6,11)，(5,11,6).

当(2φ(y)-3)(2φ(z)-3)=25时，有φ(y)=2,φ(z)=14或φ(y)=14,φ(z)=2或φ(y)=4,φ(z)=4.由于方程φ(m)=14无正整数解，因而只需讨论φ(y)=4,φ(z)=4的情形.经计算，此时方程(1)无正整数解.

情况2.8.4φ(x)=6.

此时，方程(1)可化为

于是有0≤(φ(y)-1)(φ(z)-1)≤7.

当(φ(y)-1)(φ(z)-1)=0时，φ(y)与φ(z)中至少有一个为1.结合φ(x)=6可得，此时方程(1)无正整数解.

当(φ(y)-1)(φ(z)-1)=2,4,6时，φ(y)与φ(z)中至少有一个不成立，因而此时方程(1)无正整数解.

当(φ(y)-1)(φ(z)-1)=1,3,5,7时，φ(y)与φ(z)中至少有一个满足有φ(m)=2，结合φ(x)=6，只需讨论φ(x)=6,φ(m)=2这一情况就可确定方程(1)的正整数解情况.此时，φ(x)=6,φ(m)=2正好与情况2.8.2中当(φ(y)-3)(φ(z)-3)=9时确定方程(1)的正整数解所用的φ(x)=6,φ(m)=2相同，由此可得，此时方程(1)无正整数解.

对以上所有情况的讨论进行总结可得方程(1)的所有正整数解.】

[1]吕志宏.两个数论函数及其方程[J].纯粹数学与应用数学，2006，22(3)：303.

[2]ERDÖSP．Onthenormalnumberofprimefactorsofp-1andsomerelatedproblemsconcerningEulerfunctionφ(n)[J].Quart J Math,1935,6(1):205．

[3]WOOLRIDGEK．ValuestakenmanytimesbyEulerfunctionφ(n)[J].Proc Amer Math Soc,1979,76(2):229．

[4]左可正.含欧拉函数不定方程的可解性探讨[J].黄石理工学院学报，2008，24(2)：49.

[5]孙翠芳，程智.关于方程φ(xyz)=2(φ(x)+φ(y)+φ(z))[J].数学的实践与认识，2012，42(23)：267.

[6]ROSENKH.Elementary Number Theory and Its Applications[M].5thed.UpperSaddleRiver,NewJersey:PearsonEducatinInc,AddisonWesley,2005.

(责任编辑马宇鸿)

The positive integer solutions of diophantine equation φ(xyz)=5(φ(x)+φ(y)+φ(z))

GUAN Chun-mei1,WU Xing-xing2,ZHANG Si-bao1,XI Xiao-zhong3

(1.School of Mathematics and Statistics,Kashgar University,Kashgar 844008,Xinjiang,China;2.CollegeofMathematicsandSystemScience,XinjiangUniversity,Urimqi830046,Xinjiang,China;3.InstituteofMathematicsandComputerScience,YichunCollege,Yichun336000,Jiangxi,China)

Thesolvabilityofthediophantineequationφ(xyz)=5(φ(x)+φ(y)+φ(z))isstudiedinthispaper,andallpositiveintegersolutionsoftheequationareobtainedbyusingtheelementarymethod,whereφ(n)isanEulerfunction.

Eulerfunction;diophantineequation;positiveintegersolution;elementarymethod

10.16783/j.cnki.nwnuz.2016.04.005

2015-01-16;修改稿收到日期:2015-06-22

国家自然科学基金资助项目(11201411)

官春梅(1976—)，女，湖北竹山人，讲师，硕士.主要研究方向为基础数学.

E-mail:1603454244@qq.com

O156

A

1001-988Ⅹ(2016)04-0017-05