基于流动性调整的高频协方差阵的估计及其应用研究
刘丽萍,马 丹
基于流动性调整的高频协方差阵的估计及其应用研究
刘丽萍1,马 丹2
(1.贵州财经大学数学与统计学院,贵州贵阳,550025;2.西南财经大学统计学院,四川成都,610071)
金融资产交易往往不具有时间的一致性,采用高频数据估计协方差阵时需要避免由于异步交易导致的“Epps”效应。常用的时间刷新技术能够解决异步交易问题,但随着资产数量增加,样本量会迅速减少。本文介绍了基于流动性调整的双频协方差阵估计方法(RnBTSCOV),该方法可减少数据量的损失,在不对参数施加任何限制的情况下,提高估计精度。将该方法应用到投资组合中与常用的已实现协方差阵和双频协方差阵进行对比分析,研究发现RnBTSCOV方法在所有的标准下具有更好的表现。
双频协方差阵;基于流动性调整的双频协方差阵;等比例风险投资组合
0引言
自Markowitz创立现代组合投资理论以来,组合投资选择模型大多建立在精确估计协方差阵的前提之上。如何对投资组合协方差矩阵进行精确估算,已成为组合投资和风险管理等相关领域研究的热点和难点问题。
最近二十年,统计学家们对用实时交易数据(也称为高频数据)估计组合协方差的方法,展开了广泛而深入的研究。由于金融市场总是存在价格离散性、买卖报价弹性等市场微观结噪声,当数据采样频率提高时,微观结构噪声的影响随之增大,这将使“已实现协方差阵”(Andersen 等,2003)[1]等基于二次变差理论的一些估计方法,不再是资产协方差矩阵的无偏和一致估计量。因此,近年来理论界围绕如何降低市场微观结构噪声的影响等问题,提出了多种“修正的已实现协方差阵”估计方法,主要可以归纳为稀疏抽样和连续光滑函数两大类。稀疏抽样是通过降低抽样频率来减少微观结构噪声的影响的,主要方法包括最优抽样频率(Voev和Lunde,2007)[2]和低抽样频率(de Pooter和Martens,2008)[3]两种。稀疏抽样虽然降低了微观结构噪声,但采样频率的降低会损失有用的信息。另一类方法则通过引入连续光滑函数,对高频数据进行光滑处理来减少微观结构噪声的影响,例如Zhang等(2005,2011)[4][5]提出的利用子样本区间进行平均降噪处理的双频协方差矩阵(TSCOV);Barndorff-Nielsen等(20011)[6]提出的通过引入核函数来修正微观结构噪声的多元核光滑协方差矩阵(KCOV);Christensen等(2010)[7]利用取值范围为0到1之间的连续光滑函数对高频数据进行光滑处理,得到的预平均降噪协方差矩阵(PCOV)等;这些都属于基于连续光滑降噪的协方差阵估计方法。当资产价格只受到市场微观结构噪声的影响时,这类基于平滑降噪处理的方法,能够得到资产价格波动的稳健估计量,并具有最优的收敛速度。
值得注意的是,在金融市场上各种金融资产往往并不在统一的时间进行交易。例如,中国证券市场是一个指令型驱动市场,当买卖报价被交易终端撮合时才能发生交易,而买卖报价是否能被撮合以及撮合时间是随机的,投资者在实时行情中观测到的交易不具有同步性。在数据以日或月等低频率采样时,这种时间上的不一致性不会对分析产生影响。但当研究的视角转向交易过程的内部资产价格动态变化时,异步交易将导致原本并不相关的资产之间产生某种联系。特别是随着交易频率的增加,会使得协方差矩阵中的元素大量为0,即出现Epps效应,导致直接使用高频数据估计的协方差矩阵是有偏误的(Epps ,1979)[8]。
在高频协方差阵的各类估计方法中,通常将非同步交易问题放在市场微观结构噪声的框架下进行研究,较少有专门的讨论。使用平滑降噪方法估计协方差阵时,需要先通过一种“刷新时间采样”技术来实现同步交易。其具体方法是,第一个刷新的时间对应着第一次所有股票都发生交易的时间,随后的刷新时间为所有股票再次发生交易的时间,该过程重复进行,直到该时间序列的结束(Harris,1995)[9]。在最近的研究文献中,AÏT-Sahalia等(2010)[10]用刷新时间采样方法估计资产组合的协方差阵。Zhang(2011)【5】提出的TSCOV估计方法,也使用刷新时间采样的方法来得到同时交易的样本。刷新时间采样是一种直观、简单易行的数据处理方法,但在交易频率很高的情况下,组合中的资产同时交易的时间并不多,用刷新时间采样意味着会损失大量的数据信息。尤其是当资产的维度较高,而不同资产的日内交易频率又存在较大差异时,会使得协方差阵的估计效率很低(Rosenthal和Zhang,2011)[11]。特别是2006-2010年,中国证券市场几乎所有的股票均进行了股权分置改革,由于每个股票的股改时间并不一样,当计算协方差矩阵时,通常会将因股改或者其它原因停止交易的时段剔除。若再用“刷新时间采样”方法得到每个交易日内的共同交易,将使样本量进一步减少,并且随着组合中资产数量的增加,样本量会快速降低。大量缺失数据的存在,促使我们对高频协方差矩阵的一些估计问题进行重新审视,其中之一是如何提高数据的利用效率。
从金融市场交易组织行为和交易过程内在机理的角度,金融资产的交易速度与流动性具有密切关系,它是反映流动性的重要维度(苏冬蔚和麦元勋,2004)[12]。金融资产按照流动性分类后再计算协方差阵,可能是一种减少数据信息损失的有效方法。我们使用一种基于流动性调整的分块策略对协方差阵估计方法进行调整,挖掘高频数据中的信息,提高协方差阵的估计效率。以双频协方差矩阵TSCOV为例,其基本思路是按照流动性对资产进行分组,分别估计每组资产对应的TSCOV,然后以一系列小块的TSCOV来构造整个组合的TSCOV。该方法能够减少数据的损失,但存在的问题是:基于流动性调整的分块估计的协方差矩阵与TSCOV估计一样,不能保证估计得到的协方差阵具有正定性。即使得到的每小块协方差阵都是正定的,由一系列小的协方差阵重组得到的组合协方差阵也不一定是正定的。协方差矩阵的正定性是一个很重要的理论性质,当使用协方差矩阵进行组合选择或者风险管理时,如果协方差矩阵不具有正定性,组合优化问题将变得非常困难。为了确保协方差阵的正定性,本文考虑采用特征值处理法对其进行校正。
本文结构安排如下:第一部分介绍TSCOV估计方法并且分析采用刷新时间采样时的数据损失情况。第二部分介绍本文所采用的分块策略和正则化技术,提出基于流动性调整的双频协方差阵RnBTSCOV估计方法。第三部分将RnBTSCOV方法应用到投资组合中,与TSCOV和RCOV方法进行了对比分析。第四部分是本文的结论。
1 TSCOV估计及数据损失分析
1.1 TSCOV估计方法
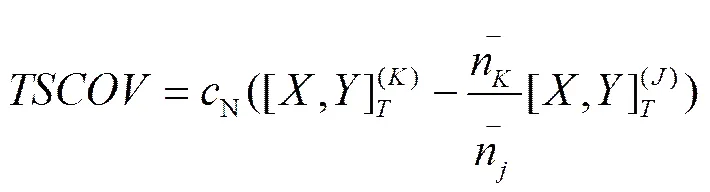
(2)
其中,
1.2 数据损失分析
当观测值的个数没有比维数大很多时,刷新时间抽样有可能使高维的协方差阵的估计无效,从而导致维数诅咒问题。为了说明这一点,我们考虑p个资产,设每个独立的交易过程具有相同的泊松到达率。将定义为所有资产至少都发生一次交易的最长等待时间的期望。因为,所以:
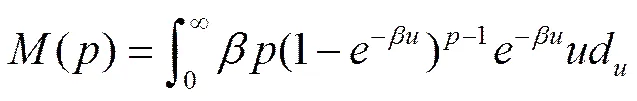
(4)
图1描述的是采用刷新时间方案时,随着资产数目的增加数据的损失情况,它给出了L(p)和p之间的关系。从图1可见,随着资产数目增加,数据损失率迅速提高。当资产数目p分别为2、10和100时,数据损失率分别达到了33%、66%和81%。
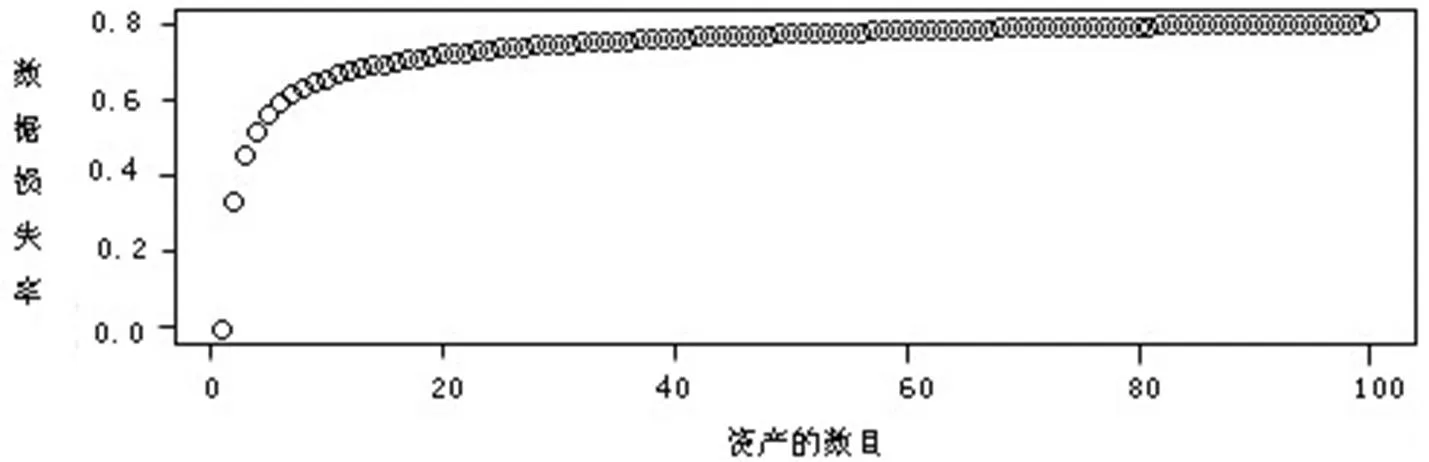
图1 采用刷新时间采样方案时,数据的损失情况示意图
2基于分块策略和正则化方法的RnBTSCOV
2.1基于分块策略的协方差矩阵

从矩阵分块的角度,(5)式可以看成是由若干个子协方差阵构成的矩阵,例如由左上角的k行k列元素构成的矩阵是前k个资产的协方差阵;右下角的(p-i+1)×(p-i+1)个元素构成的协方差阵是后p-i+1个资产的协方差阵。这意味着,将协方差矩阵按照一定方法划分为若干块,每块子矩阵都是所对应的金融资产的协方差阵。
显然,刷新时间抽样导致数据损失的原因在于,各个资产的流动性不同,有些资产流动性强,交易非常活跃,有些资产交易则比较冷清。利用分块策略估计协方差矩阵是根据资产流动性对组合中的资产进行分类,将流动性相近的资产划分为一类,分别估计其对应的协方差阵。然后将所有的资产组合相结合,形成一个新的协方差阵,而该协方差阵的每一块本身就是一个子协方差阵。这种分块估计的基本思想可以表述为:将p个资产按照流动性从高到低进行排序的,即第1个资产的流动性是最高的,第p个资产流动性最低。将流动性最高的k个资产分为一类,其协方差记为:
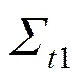
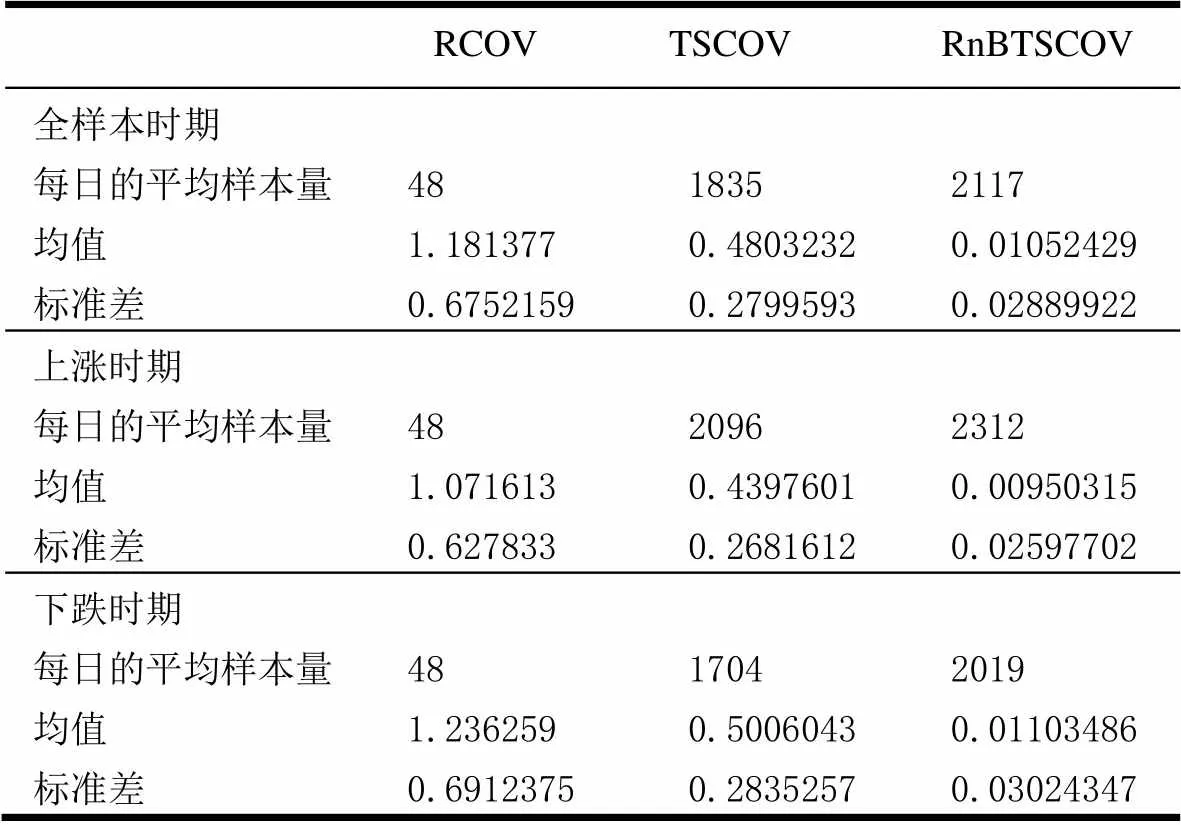
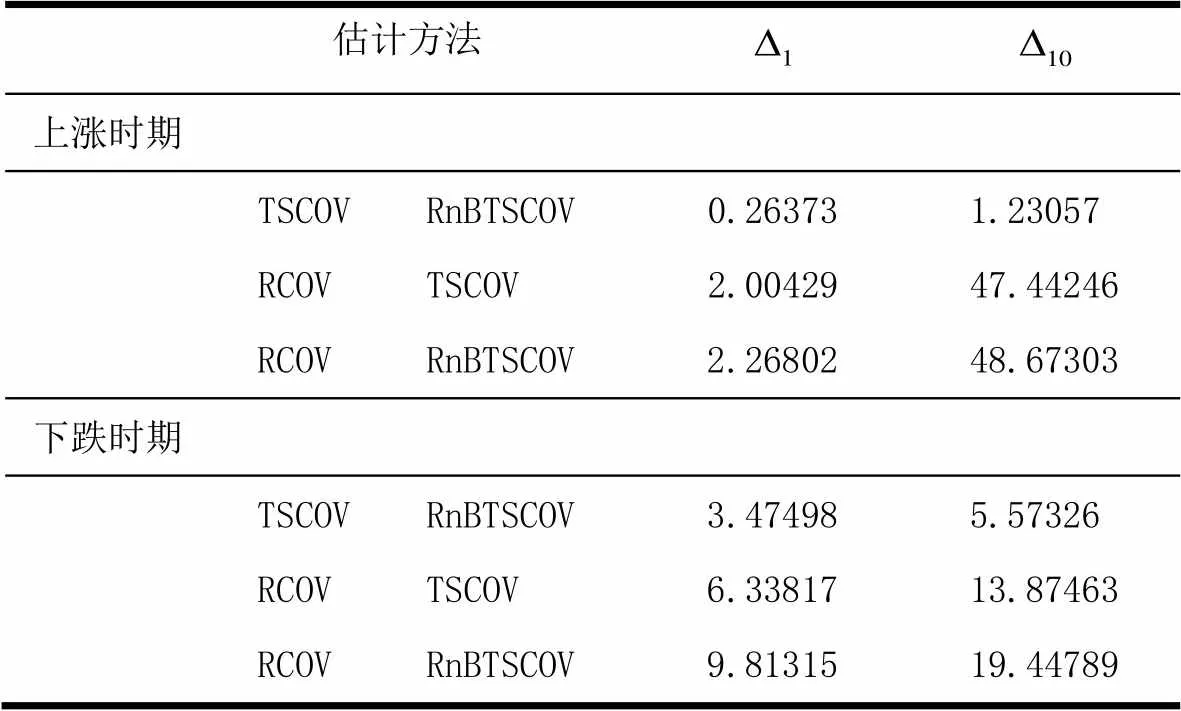
采用TSCOV方法估计(6)式时,仅需要对k个资产进行同步交易处理,而并不需要对p个资产进行同步化处理。由于这k个资产具有相类似的流动性,并且k 图2以9个资产为例描述了采用分块策略的基于流动性调整的高频协方差阵估计方法。第一步,将9个资产按照流动性的高低,从左到右从上到下进行排序,估计其TSCOV,得到图2中的块1。块1是基于对所有资产实施同一刷新时间抽样方案后估计得到的,将其作为分块估计量的基准记为矩阵1。第二步,按照流动性高低将资产划分为三组,这三组分别为较高流动性、中等流动性和较低流动性,每组有三个资产。先将流动性为中等和较低的两组资产结合,估计其TSCOV,记为块2并替代矩阵1中与其位置相对应的元素,得到矩阵2。第三步,将流动性为中等和较高的两组资产组合估计其TSCOV,记为块3并替换矩阵2中对应位置的元素,得到矩阵3。第四步,估计块4,其对应的是较低流动性资产的TSCOV,替换矩阵3对应位置的元素,得到矩阵4。第五步,估计中等流动性资产的TSCOV,记为块5,替换矩阵4对应位置的元素,得到矩阵5。最后,估计较高流动性资产的TSCOV,记为块6,并替换矩阵5对应位置的元素,得到矩阵6,即图2右侧显示的最终矩阵:采用分块策略得到的基于流动性调整的9个资产的BTSCOV。 图2 分块策略视图 BTSCOV比最初的TSCOV(块1或矩阵1)更加精确。这是因为BTSCOV中位于对角块上的元素,即属于块4、5、6的元素,都是基于三个资产的刷新时间采样来估计的,相比于原先的基于9个资产的刷新时间采样而言,大大减少了数据量的损失,提高了估计精度。对于位于非对角块上的元素而言,其中属于块2和3的元素是基于6个资产的刷新时间采样而估计的,相比于9个资产的刷新时间采样而言,同样减少了数据量的损失,提高了估计精度;而BTSCOV中的块1为未被替换的部分,其估计精度不变。因此基于分块策略的BTSCOV矩阵中的每块协方差阵的估计精度并不比最初的TSCOV(块1或矩阵1)的估计精度差,所以其估计更加的精确。 如前文所述,BTSCOV的每一块估计的都是TSCOV,都是在刷新时间采样的基础上估计的,同TSCOV估计的理论基础实际上是一致的。这种基于流动性调整的分块策略,在不对协方差阵的估计实施任何结构限制的情况下,增加了样本量,从而提高了估计精度。 根据资产的流动性对其进行分组时,还需要考虑分组数目和数据损失率之间的关系,回顾前面的描述,在K类资产的情况下,数据损失函数为: 下图3描述的是随着资产分组数目的增加,数据的损失情况。由图3知随着分组数目的增加,数据损失率在减少,分块使得估计效率得到了显著的提高,例如:当资产数目p=100,分为10类时,数据的损失率是66%而不是没有分块时的81%。 2.2 协方差阵的正则化处理方法 由前文我们知道,采用TSCOV方法估计得到的协方差矩阵不一定是正定的,由其构造的基于流动性调整的高频协方差阵估计量BTSCOV也不一定是正定的。为保证BTSCOV具有正定性,可以利用正则化技术对协方差阵进行修正(Ledoit 和Wolf (2004), Qi 和Sun (2006))。本文采用“特征值处理法”对BTSCOV进行正则化处理,该方法是由Laloux, Cizeau, Bouchaud和Potters(1999)提出的随机矩阵理论发展而来的正则化方法,它沿用了Stein (1977)最初提出的特征值收缩法的思想。 特征值处理法利用随机矩阵理论来决定特征值的分布,特征值的分布函数为q的函数,q为观测值N相对于维数p的比例,即q=N/p。在独立资产的原假设下,相关性矩阵是一个单位矩阵,最大的特征值,这里为1(Laloux, Cizeau, Bouchaud和 Potters(1999))。 特征值处理法是将实证得到的相关矩阵的特征值,与资产相互独立的假定下的随机矩阵的特征值相比较,来识别那些偏离噪声,反映市场信息的特征值。它的主要思想是:在去除噪声对应的特征值的同时,尽量保存真实的信息对应的特征值,因为噪声对应的特征值是不包含真实信息的,它们基本上没有什么意义。为了区分出实证相关矩阵中的噪声部分和非噪声部分,我们把它分为两个部分:一部分是符合随机矩阵性质的,被视为“噪声”;另一部分是偏离随机矩阵预测的差异部分,被视为“市场信息”。根据对随机矩阵理论值的预测,我们可以确定理论上的最大值,即为理论上的最大值。根据这个范围,我们就可以区分出“市场信息”与“噪声”。首先根据谱分解方法计算出实证的相关矩阵C的特征值,即:,其中是矩阵的特征向量,是由矩阵的特征值构成的对角矩阵。然后将特征值按大小排序()。最大的特征值会远远大于随机矩阵理论上的预测值,偏离了随机矩阵预测的部分,显然违反了“白噪音”的假定,被认为是市场信息。去掉该特征值,然后重新计算出,,将其作为市场的中立方差,然后再根据重新计算出。 (9) 3.1 协方差矩阵的估计及其描述性统计分析 本文采用的数据是沪深300指数的6只大盘股:中国石化、招商银行、中国联通、上海汽车、中海发展和宝钢股份的实时交易数据。数据期间为2005年1月4日至2009年4月30日,所有数据均来自CSMAR数据库。剔除样本股票中交易缺失的数据后,6只股票都有交易的天数为825天。将全部样本划分为估计和预测两个部分,其中,估计窗口长度T=525,预测窗口长度N=300,预测区间是从2007年12月24日至2009年4月30日。在预测样本区间内,中国股市经历了大幅度的下跌和一定幅度上涨,因此将整个预测时期划分为下跌和上涨两个阶段,其中2007年12月24日至2008年11月20日为下跌时期,2008年11月21日至2009年4月30日为上涨时期。 在估计股票的基于流动性调整的双频已实现协方差阵RnBTSCOV时,首先按照交易频率将这六支股票分组,由前文的描述,我们知道数据的损失率会随着分组数目的增加而减少。这里,为了得到更加精确的协方差阵,我们将这六支股票两两组合分成了3组。由表1可知,日内交易频率最高的一组为中国联通和中国石化,其次是宝钢股份和招商银行,最后是上海汽车和中海发展。按照前文所述的基于流动性调整的分块策略,分别估计这三组股票的的TSCOV,形成BTSCOV,然后对其进行正则化处理,得到这六支股票的RnBTSCOV。 表1 各个股票的描述性统计分析 注:(*)E+10意味着小数点向后移动10位 表2给出了预测的全样本时期、上涨时期和下跌时期的RCOV、TSCOV、RnBTSCOV的描述统计量。需要说明的有两点:首先计算RCOV时,我们的采样频率为5分钟;其次由于得到的TSCOV不一定是正定的,所以后文的6支股票的TSCOV估计量是经过正则化处理后得到的。 表2 预测的协方差阵的统计特征 从表2中我们发现基于流动性调整的RnBTSCOV估计量,无论是在全样本时期、上涨时期还是在下跌时期,其每日的平均样本量最大,并且该估计量的均值和标准差最小。从而说明了根据资产的流动性对其进行分组,进而采用分块策略估计高频数据的协方差阵时,在不对参数施加任何限制的情况下,减少了数据损失,提高了估计精度。 3.2 协方差矩阵在投资组合中的应用研究 3.2.1 高频协方差矩阵的预测 将高频协方差阵应用在投资组合时,预测模型的选择非常的重要,本文采用了基于乔列斯基分解的ARMA模型(CF-ARMA(2,1))。首先对协方差矩阵进行乔列斯基分解,然后对其乔列斯基分解因素建立ARMA(2,1)模型。这样处理的目的是为了保证预测的协方差阵仍然是正定的。CF-ARMA(2,1)模型可以表示为: 在估计和预测高频协方差阵时,采用滚动时间窗方法。以交易策略为每日更新组合权数为例,由于估计窗口长度T=525,预测窗口长度N=300,计算方法为:第1次的样本区间为t=1,2,…,525,用该样本估计波动模型,预测第526天的协方差阵,并根据投资组合模型计算该天组合中各资产的权数和组合收益。保持样本区间长度不变,将样本时间向前推移1天,得到第2次样本时间区间为t=2,3,…,526,重新估计波动模型,得到第527天的协方差阵预测,用预测的协方差阵计算组合权数和组合收益。重复以上步骤,直到t=301,302,…,825,计算第826天的权数和组合收益。这样,共得到300个投资组合的样本。 3.2.2 投资组合的构建 对协方差矩阵的比较和分析主要是从投资组合的效率角度展开的,本文将采用De Pooter等(2008)提出的两条标准来评价不同协方差阵估计方法所得的投资组合:一是从反映组合风险与收益关系的Sharpe比率的角度进行比较;二是从效用函数角度对投资组合的经济福利进行比较。 在构造投资组合时,方差最小或者在收益约束下方差最小是常用的目标函数,但收益或者方差的微小变化,会引起组合权数的较大波动。为避免组合权数的不稳定性对分析结果的影响,本文采用的是等比例风险方法来构建投资组合(Maillard等,2010),该方法通过调整权数使每个资产在投资组合中的风险比例相等。当资本市场不允许卖空时,该组合权数满足: 3.2.3 各投资组合的波动和收益分析 由于中国证券市场不允许主板市场股票做空交易,下跌时期的组合平均收益为负,并且在下跌时期大部分Sharpe比率为负,不具有比较意义,因此表3只给出了上涨时期的Sharpe比率。 表3 不同投资组合的平均收益、组合波动以及Share比率 表3列出了三种投资组合在上涨和下跌时的平均收益及组合波动。在上涨时期,平均收益最大的是RnBTSCOV估计量构造的投资组合,并且该组合的波动最小,Sharpe比率值最大。在下跌时期,所有组合均得到负收益,其中由RnBTSCOV构造的投资组合损失最小,而由RCOV构造的组合损失最大,RCOV对应的组合波动也最大。总体而言,RnBTSCOV较TSCOV的效果要好,这是因为该方法在计算协方差阵时,减少了数据信息的损失,使得估计更加的精确。RCOV的表现是最差的,这可能是由于市场微观结构噪声和非同步交易的影响。 考虑到表3只给出了上涨时期的Sharpe比率,即采用固定时间长度作为时间窗宽计算的Sharpe比率。而在整个样本期间,市场经历了上涨和下跌行情,当时间窗口发生变化时,Sharpe比率必然会随之变化。为了反映全样本期间的Sharpe比率的变化情况,我们采用滑动平均的方法计算动态Sharpe比率。记m为平滑窗宽,和分别是在区间[i,i+1,…,i+m]中组合的平均收益和方差。该区间的Sharpe比率可以写为: 图4绘制了窗宽m=100时,四个投资组合的Sharpe比率变化情况。从图4可以看出,RnBTSCOV组合的动态Sharpe比率大于其它两个组合的动态Sharpe比率,说明了整体而言,用RnBTSCOV估计高频数据的协方差阵要优于其它两种方法。而TSCOV的动态Sharpe比率没有显著大于RCOV的Sharpe比率,二者基本上差不多。 3.2.4 各投资组合经济福利的比较 其中,Δ代表了两种估计方法在组合管理方面的应用价值之差。若估计方法的改进引起了组合表现的提升,Δ表示投资者为了获得这种组合表现提升而每日愿意牺牲的最大效用,此时Δ为正。采用的效用函数为: (15) 表4 不同投资组合的年化效用函数 本文提出了一种基于流动性调整的高频协方差阵估计量——RnBTSCOV。RnBTSCOV估计量由一系列小块的TSCOV构造而成,由于每块协方差阵都是基于不同的抽样频率来估计的,所以基于流动性调整的高频协方差阵估计方法减少了数据量的损失。为了进一步说明该估计量的有效性,本文还将RnBTSCOV应用到投资组合中,与常用的RCOV和TSCOV方法进行了对比分析,研究发现RnBTSCOV构造的组合的平均收益最高、组合波动最小,其动态Sharpe比率最高,并且相对于其它的高频协方差阵估计方法而言,该方法还获得了超额的平均年化收益率。检验证明,基于流动性调整的RnBTSCOV估计方法在所有的比较标准下都具有最好的表现,该方法在不对参数施加任何限制的情况下,提高了估计精度。 [1] Andersen T.G., Bollerslev T., Diebold F.X, et al. Modeling and forecasting realized volatility [J]. Journal of Econometrics, 2003, (71): 579-625. [2] Voev V, Lunde A. Integrated Covariance Estimation Using High-Frequency Data in the Presence of Noise[J]. Journal of Financial Econometrics, 2007,(5):68–104. [3] De Pooter M., Martens M. P., Van Dijk D. J. Predicting the daily covariance matrix for S&P 100 stocks using intraday data - but which frequency to use[J]? Econometric Reviews, 2008,(27):199–229. [4] Zhang L., Mykland P.A, A¨ıt-Sahalia Y. A tale of two time scales:determining integrated volatility with noisy high-frequency data[J]. Journal of the American Statistical Association 2005, (100): 1394–1411. [5] Zhang, L. Estimating covariation:Epps effect, microstructure noise[J], Journal of Econometrics,2011,(160) .:33-47. [6] Barndor-Nielsen O. E., Hansen P., Lunde A., et al. Multivariate realised kernels: consistent positive semi-definite estimators of the covariation of equity prices with noise and non-synchronous trading [J].Journal of Econometrics, 2011, (162):149 – 169. [7] Christensen K., Kinnebrock S., Podolskij M .Pre-Averaging Estimators of the Ex-Post Covariance Matrix in Noisy Diusion Models with Non-Synchronous Data[J]. Journal of Econometrics, 2010,(159):116—133. [8] Epps T. Comovement in Stock Prices in the Very Short Run[J]. Journal of the American Statistical Association, 1979, (74):291–298. [9] Harris F., T. McInish G., Shoesmith, et al. Cointegration, error correction, and price discovery on infomationally linked security markets[J]. Journal of Financial and Quantitative Analysis 1995,(30):563–581. [10] AÏT-Sahalia Y., Fan J., Xiu D. High-Frequency Covariance Estimates with Noisy and Asynchronous Data. Journal of the American Statistical Association[J], 2010,(105):1504–1517. [11] Rosenthal, Dale W. R., Zhang L., et al. Index Arbitrage and Refresh Time Bias in Covariance Estimation, working paper, 2011. [12] 苏冬蔚; 麦元勋; 流动性与资产定价:基于我国股市资产换手率与预期收益的实证研究.经济研究,2004,(2):95—105. [13] Ledoit O., Wolf M. A well-conditioned estimator for large-dimensional covariance matrices[J]. Journal of Multivariate Analysis, 2004, (88):365–411. [14] Qi H., Sun D. A Quadratically Convergent Newton Method for Computing the Nearest Correlation Matrix SIAM [J].Journal of Matrix Analysis and Applications, 2006,(28): 360–385. [15] Laloux L., Cizeau P., Bouchaud J., et al. Noise Dressing of Financial Correlation Matrices[J].Physical Review Letters, 1999, ( 83): 1467 – 1470. [16] Stein C. Lectures on the theory of estimation of many parameters,” in Studies in the Statistical Theory of Estimation, Part 1, eds. Ibragimov, I. and Nikulin, M., Proceedings of Scientific Seminars of the Steklov Institute,no. 1977,(74): 4–65. [17] Chiriac R., Voev V. Long memory modeling of realized covariance matrices. Working Paper, University of Konstanz, 2007. [18] LIU Q. On Portfolio Optimization: How and when do we benefit from high frequency data. Journal of Applied Econometrics [J], 2009, 24(4):560–582. [19] Maillard S., Roncalli T., Teiletche J. On the properties of equally weighted risk contributions portfolios [J], Journal of Portfolio Management, 2010, 36(4):60–70. [20] Fleming J., Kirby C., Ostdiek B. The economic value of volatility timing using realized volatility [J], Journal of Financial Economics, 2003, (67): 473–509. Estimation and Application Study on Covariance Matrix of High Frequency Data Based on Liquidity Adjustment (1.School of Mathematics and Statistics, Guizhou University of Finance and Economics, Guiyang 550025, China; 2. School of Statistics, Southwest University of Finance and Economics, Chengdu 610074, China) The covariance matrix of financial assets plays an important role in portfolio management. Because high-frequency data contains richer information, an increasing number of scholars began to consider using high-frequency data to estimate the covariance matrix of financial assets. However, the trading time of financial assets is usually inconsistent. When using high-frequency data to estimate the covariance matrix, we need to avoid “Epps” effect which is caused by asynchronous transactions. The refresh time technology is commonly used to solve asynchronous transaction problems. However, with the increasing number of assets the sample size will decrease rapidly. To reduce the amount of data loss and improve the estimation efficiency of covariance matrix, we use blocking strategy and regularization approach to estimate TSCOV, and propose RnBTSCOV estimator which is based on liquidity adjustment. The blocking strategy starts by ordering assets in the covariance matrix according to transaction frequency, with the most liquid assets in the top left corner and the least liquid assets in the bottom right corner. This initial step ensures that subsequent blocks will group assets with similar transaction frequencies. We further divide assets into liquidity-based clusters. Asset clusters are then combined to form a BTSCOV at last, where each block itself is a covariance matrix. Because TSCOV is not necessarily positive definiteness, the BTSCOV, which is reconstructed by a series of small TSCOV, is also not necessarily positive definiteness. Positive definiteness of the covariance matrix is a very important theoretical nature. When high frequency covariance matrix applies in the portfolio and risk management and if the covariance matrix does not have positive definiteness, combinatorial optimization problem becomes very difficult. In order to ensure positive definiteness of the covariance matrix, we adopted the “Eigenvalue Cleaning” technique and then obtained the “RnBTSCOV”. We apply the RnBTSCOV estimator in portfolio, and compare it with RCOV estimator and TSCOV estimator. We find that the portfolio, which is constructed by the RnBTSCOV, has the highest average yield. In addition, the least volatile and dynamic Sharpe ratio are the highest.In comparison with other high-frequency covariance matrix, RnBTSCOV method has the average annual yield. In summary, RnBTSCOV estimator performs better under all the evaluation criteria. The estimator reduces data loss, and clearly increases the estimator’s efficiencywithout imposing any additional structure on the covariance estimate. TSCOV;RnBTSCOV;Equally weighted risk contribution portfolio 中文编辑:杜 健;英文编辑:Charlie C. Chen F830.9 A 1004-6062(2016)02-0076-08 10.13587/j.cnki.jieem.2016.02.009 2012-10-10 2013-11-17 国家社会科学基金资助项目 (10XTJ0001);贵州财经大学人才引进资助项目 刘丽萍(1984—),女,山东菏泽人,副教授,统计学博士,主要从事金融数量分析研究。
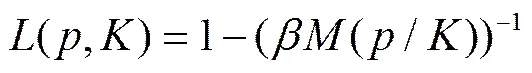
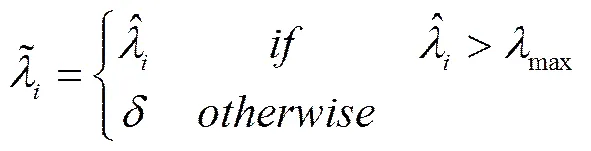

3 协方差矩阵的估计及其在投资组合中的应用研究

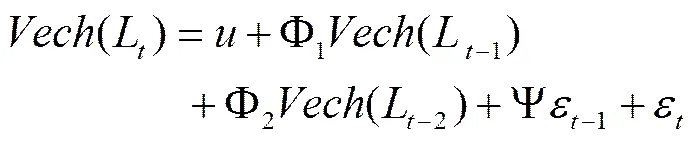
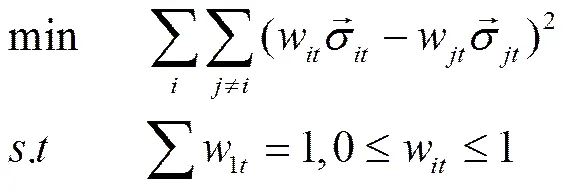

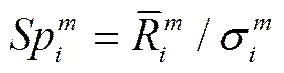
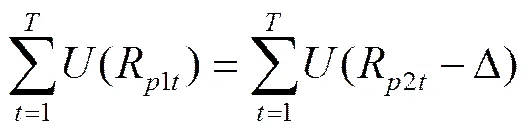
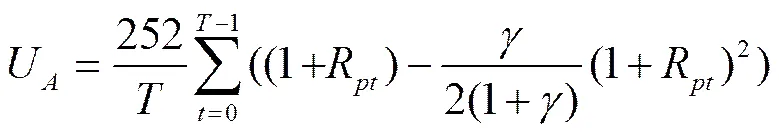
4 结论

