受控旋转弹飞行动力学建模和稳定性分析*

甄亭亭 徐鉴 温建明

（同济大学航空航天与力学学院，上海 200092）

受控旋转弹飞行动力学建模和稳定性分析*

甄亭亭 徐鉴 温建明

（同济大学航空航天与力学学院，上海 200092）

选取带有控制系统的旋转弹为研究对象，考虑到控制环节不可避免的时滞及气动非线性效应，从理论上进一步完善了旋转弹动力学模型.从模型的特征方程出发，以时滞、控制增益为分岔参数，对系统的零平衡点稳定性进行了分析，得到平衡点失稳后发生Hopf分岔的临界参数值，并在理论预测的情况下数值模拟了攻角和侧滑角在不同情况下的失稳情况以及Hopf分岔周期解振幅随分岔参数的变化情况.数值结果表明了理论预测的正确性，时滞虽未改变旋转弹锥形运动方式，但是却大幅度的减小了稳定飞行控制增益的取值范围，因此在旋转弹姿态稳定性系统设计过程中时滞的影响不可忽略.

旋转弹，时滞，控制增益，稳定性，Hopf分岔

引言

旋转弹是指弹体在飞行中绕自身纵轴连续旋转的一类飞行器，广泛用于常规兵器、制导兵器、战术导弹等.随着常规兵器制导化及旋转制导弹药的发展，研究带有控制系统的旋转弹运动系统稳定性具有重要意义.但是在受控系统中，控制信号传输或控制设备自身存在的某些缺陷使得控制系统与执行机构之间存在时滞，于是控制系统就会成为时滞动力系统.

无时滞时的旋转弹的稳定性分析已经有了一定的研究结果.Nicolaides［1］在1953年较早的指出旋转弹体存在圆运动的特征.Murphy［2-3］针对旋转引起的陀螺效应、马格努斯效应对于无控旋转弹的稳定性的影响进行了研究；Kang，Meyer［4-6］等在分析飞行器姿态稳定性的过程中考虑了有效载荷模块导致的飞行通道耦合行为；侯鹏［7］等针对直升机地面开车过程耦合气弹动力学行为进行了分析；Zarchan，George，Garnell［8-10］提出分别在非旋转导弹俯仰通道和偏航通道设计自动驾驶仪并且成功应用于飞行器设计中；Greagh［11］则尝试将上述方法应用于旋转导弹的设计中；李克勇［12］等针对气动非线性的情况，利用李雅普诺夫一阶近似方法给出了弹道顶点锥形运动的稳定性判据；毛雪瑞［13］基于弹体的短周期运动建立了弹体的章动角运动模型，并采用李雅普诺夫一级近似方法得出了弹体章动稳定性的基本条件.

考虑受控环节不可避免的时滞对于旋转弹的稳定性影响文献并不多见.Lang，B.O.，Idan［14-15］等指出由于控制系统与执行机构之间存在时滞，俯仰通道和偏航通道之间的耦合会在其他通道产生一个多余的控制力矩.Yang［16-19］对带有自动驾驶仪的旋转导弹锥形运动的稳定性进行了研究，文中提到了时滞，但是却未分析时滞对于其稳定性的影响.

已有研究［20-21］表明在一些机械设计过程中如果不考虑时滞，就会降低控制效果，甚至会导致控制失败.近年来随着对飞行精度要求的提高，考虑动力系统中时滞的影响就显的很有必要.所以本文选取带有控制系统的旋转弹为研究对象，考虑气动非线性效应，进一步完善了旋转弹动力学模型，得出避免旋转弹发生不收敛运动的时滞及增益量的适当范围以及时滞、控制增益对于系统稳定性的影响，为旋转弹的工程设计和进一步深入研究提供理论依据.

1 旋转弹飞行动力学建模

旋转弹在空间的运动一般看成可控制的变质量系统具有6个自由度的运动.文献［18］采用具有三回路自动驾驶仪的鸭式气动布局旋转弹作为研究对象，两对鸭翼作为控制面随着弹体旋转.文中把要研究的变质量系的旋转弹当作常质量的带有薄翼的细长刚体处理，且认为旋转弹在小段时间内速度v及绕弹轴旋转速度为常值，即=0，=0，得到旋转弹的动力学方程如下：其中各字符所代表的物理含义见附录1.设航向角φ，偏航角φ，攻角α及侧滑角β很小，则有cosφ≈1、cosφ≈1、sinφ≈φ、θ=ϑ-α、φ=ψ-β，将旋转弹所受力及力矩（见附录2）代入方程（1）则简化为如下形式：

其中，

且

由于时滞τ的存在，→σc实际上是针对t-τ时刻的误差信号做出的反应，则式（3）实际上应为

文中采用文献［19］中三回路自动驾驶仪对旋转弹进行稳定控制.由三回路自动驾驶仪的工作原理可知t-τ时刻输入指令为

令加速度输入指令acy=0，acz=0，且旋转弹加速度ay=vθ，az=-vφ，整理式（5）得

将式（6）代入式（4）得到

假设在自动驾驶仪的设计过程中考虑了重力的因素，则将式（7）代入方程（2）经简化得

其中各项系数的表达式见附录三.

2 旋转弹稳定性分析

下面分析方程（8）受控回路中的时滞对弹体飞行稳定性的影响.令方程（8）可以写成如下形式

令x=0，易得（000000）是方程（9）的平衡点.取方程（9）的线性部分有

从而得到方程（10）的特征方程

即

由于A≠0，所以方程（11）无零解.令λ=μ +iω，由于特征方程（11）的复根总是以共轭复数形式出现，不妨设ω>0.我们考虑kp、kz、γ、τ满足什么样的条件时，方程（11）的所有实部μ<0.当μ= 0时，λ=iω，代入方程（12）并将方程（12）的实部和虚部分开，得到

为了便于分析，不失一般性，假定加速度器位于弹体质心位置，即c=0，此时，加速度器测量的是弹体质心实际的加速度，于是可令加速度调节增益ka=1.当阻尼回路增益kω过小时，令时滞τ和转速γ为常值时，无论kp、kz如何取值，旋转弹都将失稳.因此，根据经验我们选取了kω=0.6.通过数值模拟即可得到满足方程（13）的不同的函数曲线f （kp，kz）=0，即旋转弹保持稳定的临界曲线，如图1 （a）～（d）所示，临界曲线下面的区域则表示使系统保持稳定的kp、kz的范围.表1给出了某旋转弹相关参数.

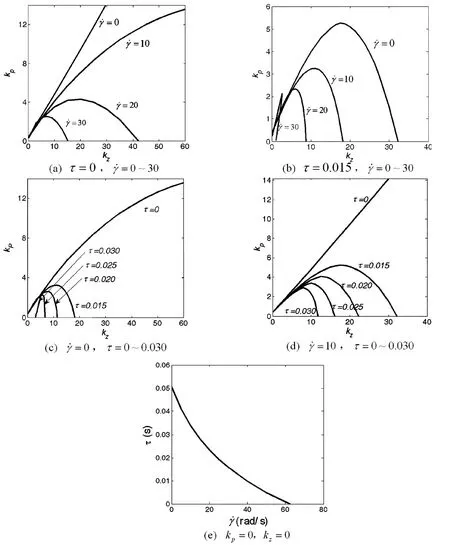
图1 临界曲线Fig.1 Critical curves

由图1（a）可知控制系统不存在时滞时，随着转速的增加，使系统保持稳定的kp、kz范围越来越小；由图1（b）可知控制系统存在时滞时，使系统保持稳定的kp、kz范围依然随着转速的增加而减小，且与图1（a）的比较可知，当系统中存在时滞τ时，使系统保持稳定的kp、kz的范围缩小的更为剧烈；由图1（c）和图1（d）可知无论弹体是否旋转，使系统保持稳定的kp、kz的范围均随着时滞τ的增大而减小；由图1（a）及图1（b）已知旋转速度的增大会减小使系统稳定的kp、kz区域，因此当弹体旋转时，时滞的加入使得kp、kz范围减小的更为剧烈.

表1 旋转弹的相关参数Table 1 Parameters of a spinningmissile

由图1（d）可知随着时滞的增加，使系统保持稳定时kp、kz的范围会减小到零这种极限情况，此时若要保持系统稳定则需要相应的调整转速γ.则令kp=0、kz=0，通过式（13）即可得到系统稳定性临界曲线f（γ，τ）=0，如图1（e）.

图1（e）表明当kp、kz均缩小为0的时候，若要使时滞继续增加，则必须相应地减小旋转速度，而当时滞达到一定值时，无论怎样调整控制增益kp、kz及转速γ系统都不能保持稳定状态.如图1（e），当时滞τ=0.051，转速γ=0，无论怎样调整控制增益kp、kz系统都将不能保持稳定.

为验证上述所得稳定区域的正确性，选取不同稳定区域中的点观察平衡点的稳定性，如图2（a）～2 （d）所示.如取图1（a）中点A（τ=0，γ=10，kz=10，kp=4）；图1（c）中点B（γ=0，τ=0.025，kz=10，kp=3. 4）；图1（d）中点C（γ=10，τ=0.03，kz=2，kp=0.2）；图1（e）中点D（τ=0.04，γ=5.5，kz=0，kp=0）.

由图2（a）～2（d）可知弹体飞行时顶部的运动轨迹随着时间收敛到平凡解，进而验证了所得稳定性临界曲线的正确性，同时表明时滞的加入并未改变旋转弹的锥形运动形式.

图2 不同点处的稳定运动曲线Fig.2 Stablemotion curves at different points

综上可知，时滞虽未改变旋转弹的锥形运动形式，但是时滞和转速都会影响使系统保持稳定的kp、kz的范围，且kp、kz的范围均随着时滞与转速的增加而减小.同时值得注意的是该时滞存在上限，当时滞超过某一值时，无论如何调整kp、kz的值系统都将失稳.所以在研究旋转弹的动力学系统稳定性过程中，考虑时滞的影响就显得很有必要.

3 旋转弹失稳运动分析

上一节我们通过数值模拟已经得到了系统（9）对应的线性系统的平衡点渐进稳定时的kp、kz区域范围.当kp、kz的值超过临界曲线进入不稳定区域时，将导致系统平衡点失稳.由于在临界曲线上存在纯虚根λ=iω，系统（9）将出现分岔.由Hopf分岔的定义可知，当临界曲线上的点满足条件时，系统发生Hopf分岔，攻角和侧滑角产生周期解的运动形式.由方程（12）可以得到

取图1（d）上一点E（τ=0.02，γ=10，kz=10，kp=2.021）为例，特征值实部存在μ=0的情况.将该点带入方程（14），得到0，即当 kp，kz穿过临界值增大时，方程（11）的特征值的实部μ由负变正.我们取E点附近数据观察方程（11）的特征值的分布情况：（1）E1：τ=0.02，γ= 10，kz=10，kp=1.9；（2）E2：τ=0.02，γ=10，kz= 10，kp=2.1；（3）E3：τ=0.02，γ=10，kp=2.021，kz=9.8；（4）E4：τ=0.02，γ=10，kp=2.021，kz=10. 2，如图3（a）～3（d）所示.

由图3（a）～3（d）可知kp、kz的值穿过临界曲线增大时，特征方程（11）的特征值的实部由负变正，与理论预测结果一致.由非线性时滞系统的Hopf分岔定理可知，当kp、kz从稳定区域经过上述稳定性临界点时，系统（9）发生了Hopf分岔.

图3 不同点处的特征值分布Fig.3 Distrib ution of eigenvalues at different points

图1（e）表示kp=0、kz=0的极限情况，此时我们以转速γ及时滞τ为分岔参数.由Hopf分岔的定义可知，当临界曲线上的点满足条件时，系统发生Hopf分岔.同理我们取图1（e）临界曲线上一点F（τ=0.034，γ=10，kz=0，kp=0）为例，得到，即当γ，τ穿过临界值增大时，特征方程（11）的特征值的实部μ由负变正，即当γ，τ从稳定区域经过 F点时，系统（9）发生了Hopf分岔.

同理我们验证了图1（c）上临界点 G（τ=0. 02，γ=0，kz=15，kp=3.967），图1（d）上临界点H （τ=0.025，γ=10，kz=6.879，kp=0）满足Hopf分岔条件.同时我们分别在E、G、H、F点附近失稳区域选取一个不同点，观察旋转弹失稳之后的运动形式：（1）Eu：τ=0.02，γ=10，kz=10，kp=2.1；（2） Gu：τ=0.02，γ=0，kz=15，kp=4.1；（3）Hu：τ=0. 025，γ=10，kz=8，kp=0；（4）Fu：τ=0.05，γ=10，kz=0，kp=0如图4（a）～4（d）所示.

图4 不同点的失稳运动曲线Fig.4 Unstablemotion curves at different points

由图4（a）～4（d）可知当增益kp、kz及时滞τ穿过临界值某些点时系统平衡点失稳发生Hopf分岔，产生周期解，且在非稳定区域内选取不同的参数值时，产生的周期解的振幅也不相同.例如，设初始扰动为(5°3°5°3°00)，图5（a）中令γ=10、τ=0.015，图5（b）中令γ=10，kp=1，分别模拟了kz取不同值平衡点失稳后攻角和侧滑角周期运动振幅随比例调节增益kp及时滞τ的变化情况.

图5 周期解振幅随参数变化的曲线Fig.5 Amplitude of periodic solution changing with parameters

图5（a）及图5（b）表明，当所取参数超过临界曲线进入非稳定区域时，旋转弹并不是立即发散，而是在一定范围内做周期性运动，随着参数远离临界值周期解振幅也随之变大，则旋转弹的命中率也随之降低.

4 结论

本文选取带有控制系统的旋转弹为研究对象.在考虑时滞及气动非线性效应下，从理论上进一步完善了旋转弹的动力学模型.以时滞τ、增益kp、kz为控制参数，数值模拟得到系统的稳定性临界曲线及平衡点失稳后的运动形式，进而得到以下结论：

（1）虽然时滞的存在未改变旋转弹锥形运动形式，但时滞和转速均会影响系统稳定时kp、kz的取值范围，并且kp、kz的取值范围均会随着时滞及转速的增大而减小.因此当弹体旋转时，时滞的存在就会使得kp、kz的取值范围缩小地更为剧烈.同时系统的时滞存在上限，即超过某一值时，无论如何调整kp、kz的值系统都将失稳.因此可以看出时滞的存在对于系统保持稳定是非常不利的，所以随着对飞行精度要求的提高，考虑控制系统时滞的影响就显得更加重要.

（2）增益kp、kz及时滞τ在穿越临界曲线上的点时会发生Hopf分岔，产生周期解，且周期解的振幅随分岔参数远离临界值而增大，从而降低了旋转弹的命中率.

1 Nicolaides JD，On the free flightmotion ofmissiles having slight configurational asymmetries，U.S.Army Ballistic Research Lab.Rept.858，June 1953

2 Murphy C H.Free-flight motion of symmetric missiles，Ballistic Research Lab.Rept.1216，Aberdeen Proving Ground，MD，1963

3 Murphy CH.Some special cases of spin yaw lock-in.Journal of Guidance，1989，12（6）：771～776

4 Kang，JY，Cochran JE.Stability criteria of slosh motion with periodicity in a spinning spacecraft.Journal of Guidance Control and Dynamics，2004，27（3）：356～364

5 Meyer R X.Coning instability of spacecraftduring period of thrust.Journal of Spacecraft and Rockets，1996，33（6）：781～788

6 Kang JY，Cochran JE.Resonantmotion of a spinning stabilized thrusting spacecraft.Journal of Guidance Control and Dynamics，2004，27（3）：356～364

7 侯鹏，杨卫东，孙东红，等.直升机地面开车过程旋翼/机体/起落架耦合气弹动力学分析.振动工程学报，2013，26（3）：318～327（Hou P，YangW D，Sun D H，et al.Aero-elastic analysis of rotor/fuselage/landing gears coupled system for helicopter during rotor starting process on the ground.Journal of Vibration Engineering，2013，26 （3）：318～327（in Chinese））

8 Zarchan P.Tactical and strategic missile guidance，5th ed.，AIAA，Reston，VA，2007：510～527

9 George M S.Missile guidance and control systems，Springer-Verlag，New York，2004：129～151

10 Garnell P.Guidedweapon control systems，2nd ed.New York：Pergamon，1980：92～151

11 Creagh M A，Mee D J.Attitude guidance for spinning vehicles with independent pitch and yaw control.Journal of Guidance Control and Dynamics，2010，33（3）：915～922

12 李克勇，赵良玉，周伟.一类旋转弹在高空的锥形运动的稳定性.动力学与控制学报，2012，10（3）：239～243 （Li K Y，Zhao LY，Zhou W.Stability of coningmotion of spinning rocket projectiles at high altitude.Journal of Dynamics and Control，2012，10（3）：239～243（in Chinese））

13 Mao X R，Yang S X，Xu Y.Coning motion stability of wrap around fin rockets.Science in China Series E：Technological Sciences，2007，50（3）343～350

14 Lange B O，Fleming A W，Parkinson BW.Control synthesis for spinning aerospace vehicles.Journal of Spacecraft and Rockets，1967，4（2）：142～150

15 Idan M，Shinma T，Golan OM.Integrated slidingmode autopilot guidance for dual-controlmissile.Journal of Guidance Control and Dynamics，2007，30（4）：1081～1089

16 闫晓勇，杨树兴，张成.基于章动运动理论的火箭弹锥形运动稳定性分析.兵工学报，2009，30（10）：1291～1296（Yan X Y，Yang SX，Zhang C.Analysis of stability for coningmotion of rockets based on theory of nutation movement.Acta Armamentarii，2009，30（10）：1291～1296（in Chinese））

17 Yan X Y，Yang SX，Zhang C.Coningmotion of spinning missiles induced by the rate loop.Journal of Guidance Control and Dynamics，2010，33（3）：1490～1499

18 Li K Y，Yang S X，Zhang C.Stability of spinning missiles with an acceleration autopilot.Journal of Guidance Control and Dynamics，2012，35（3）：774～786

19 Li K Y，Yang S X，Zhao L Y.Three-loop autopilot of spinning missiles.Journal of Aerospace Engineering，2014，228（7）：1195～1201

20 Xu J，Chung K W，Chan C L.An efficientmethod for studying weak resonant double Hopf bifurcation in nonlinear systemswith delayed feedbacks.SIAM Journal Applied Dynamical Systems，2007，6（1）：29～60

21 Xu J，Chung KW.Effects of time delayed position feedback on a van der Pol-Duffing oscillator.Physica D，2003，180：17～39

附录1 主要符号表

附录2 旋转弹所受力与力矩表达式

假设旋转弹气动轴对称，考虑气动非线性的力与力矩的表达式可有文献［12］得到：升力FLy及侧向力FLz为

的马格努斯力在速度坐标系Oyv、Oyv轴上的分量Fμy、Fμz为

*The project supported by the Key Program of the National Natural Science Foundation of China（11032009）

阻尼力矩在准弹体坐标系Oynb轴及Oznb轴上的分量Mωy、Mωz为

马格努斯力矩在准弹体坐标系Oynb轴及Oznb轴上的分量Mμy、Mμz为

静稳定力矩在准弹体坐标系Oynb轴及Oznb轴上的分量Msy、Msz为

控制力矩在准弹体坐标系Oynb轴及Oznb轴上的分量为

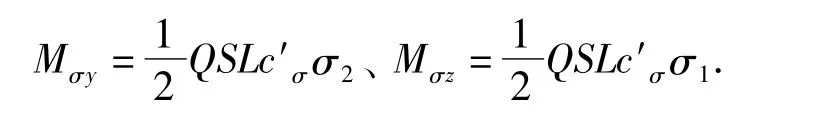
推力T及重力G在速度坐标系上的分量可参考文献［18］，利用速度坐标系与弹体坐标系、惯性坐标系之间的转换关系得到：

MODELING AND STABILITY ANALYSISOF SPINNING M ISSILE W ITH CONTROL SYSTERM*

Zhen Tingting Xu Jian Wen Jianming
（School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China）

A spinningmissile with control system was chosen as the research object in this paper.The dynamic model of the spinning missile was improved in theory by considering nonlinear aerodynamics and time delay in control segment.Setting time delay and control gains as the bifurcation parameters，stability analysis of one equilibrium pointwasmade based on the characteristic equation of thismodel.Critical Hopf bifurcation values were obtained when the equilibrium point lost its stability.Then，the instable states of the attack angle and sideslip angle were numerically simulated under theoretical prediction.Meanwhile，the amplitude of periodic solutions changing with congtrol gains and tiem delay were achieved.The numerical results indicate that the theoretical prediction is relatively reasonable.Time delaymade little change on the coningmotion of the spinningmissile，but it dramatically decreases the selectable ranges of control gains in keeping the system stable.In consequence，time delay can not be ignored for designing stability system of the spinningmissile.

spinningmissile，time delay，control gains，stability analysis，Hopf bifurcation Received 29 March 2015，revised 7 April 2015.

E-mail：xujian@tongji.edu.cn

附录3 文中相关系数的表达式

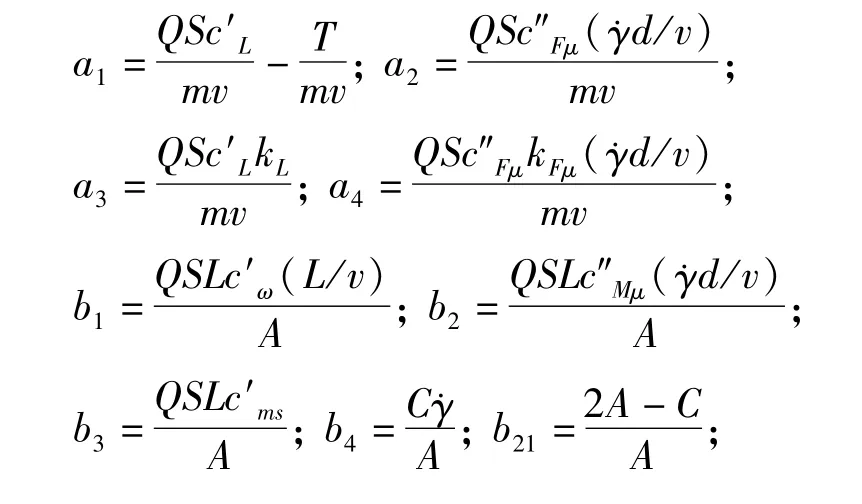
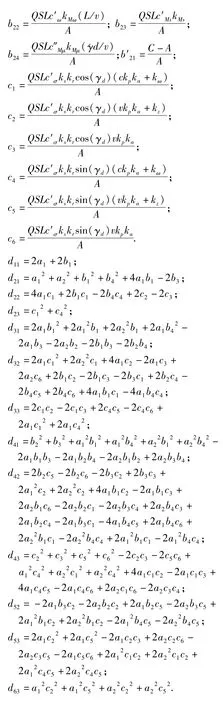
10.6052/1672-6553-2015-040

2015-03-29收到第1稿，2015-04-07收到修改稿.

*国家自然科学基金重点资助项目（11032009）

E-mail：xujian@tongji.edu.cn