品味2016年高考数列创新试题

王　维

(山东省曹县第三中学,274400)



○高考之窗○

品味2016年高考数列创新试题

王维

(山东省曹县第三中学,274400)

创新试题已成为近几年高考数学卷的一大亮点,特别是有关数列的创新试题,倍受高考命题专家的青睐.高考创新试题主要考查学生对数学问题的理解能力、抽象概括能力以及创新意识.创新试题通常以“新定义”为载体考查考生正确理解与运用新知识的能力,特别是能将所学知识与方法迁移到不同情境中,进而考查考生的理性思维与数学素养.本文仅以2016年全国各省市高考有关数列试题为例予以说明.

一、定义新数列创新题

例1(全国卷)定义“规范01数列”{an}如下:{an}共有2m项,其中m项为0,m项为1,且对任意k≤2m,a1,a2,…,ak中0的个数不少于1的个数.若m=4,则不同的“规范01数列”共有()

(A)18个(B)16个

(C)14个(D)12个

解由题意可知,必有a1=0,a8=1,a2,a3,…,a7中有3个0，3个1,且对任意k≤8,a1,a2,…,ak中0的个数不少于1的个数.

于是，可将不同的“规范01数列”列举如下:

(1)0,0,0,0,1,1,1,1;

(2)0,0,0,1,0,1,1,1;0,0,0,1,1,0,1,1;0,0,0,1,1,1,0,1;

(3)0,0,1,0,0,1,1,1;0,0,1,0,1,0,1,1;0,0,1,0,1,1,0,1;0,0,1,1,0,0,1,1;0,0,1,1,0,1,0,1;

(4)0,1,0,0,0,1,1,1;0,1,0,0,1,0,1,1;0,1,0,0,1,1,0,1;0,1,0,1,0,0,1,1;0,1,0,1,0,1,0,1.

综上可知,不同的“规范01数列”共有14个,故应选C.

评注本题是一个新定义数列创新试题,解决该题的关键是对新定义数列的正确理解与应用,同时也考查分类加法计数原理.

例2(全国卷)Sn为等差数列{an}的前n项和,且a1=1,S7=28.记bn=[lg an],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg 99]=1.

(1)求b1,b11,b101;

(2) 求数列{bn}的前1 000项和.

解(1)由题意，可得等差数列{an}的通项公式为an=n(过程略).于是有

b1=[lg 1]=0,b11=[lg 11]=1,

b101=[lg 101]=2.

(2) 设数列{bn}的前n项和为Tn,则当0≤lg an<1时,n=1,2,3,…,9;当1≤lg an<2时,n=10,11,12,…,99;当2≤lg an<3时,n=100,101,102,…,999;当lg an=3时,n=1 000,

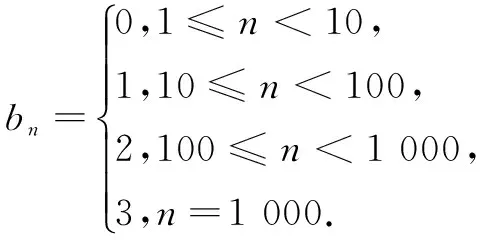
所以，数列{bn}的前1000项和为

T1000=b1+b2+b3+…+b1000

=0×9+1×90+2×900+3×1

=1 893.

评注本题定义一个新函数即取整函数(又称高斯函数)，应紧扣取整函数的定义,把数列{bn}的通项公式表示为分段函数的形式,进而使问题得以顺利解决.

二、新数列运算创新题

例3(江苏卷)设U={1,2,…,100}对数列{an}(n∈N*)和U的子集T,若T=∅,定义ST=0;若T={t1,t2,…,tk},定义ST=at1+at2+…+atk.例如，T={1,3,66}时,ST=a1+a3+a66.现设{an}(n∈N*)是公比为3的等比数列,且当T={2,4}时,ST=30.

(1)求数列{an}的通项公式;

(2) 对任意正整数k(1≤k≤100),若T⊆{1,2,…,k},求证:ST

(3)设C⊆U,D⊆U,SC≥SD,求证:SC+SC∩D≥2SD.

解(1)由题意,可得an=a1·3n-1(n∈N*).当T={2,4}时,ST=a2+a4=a2+a2·32=10a2=30,从而a2=3,所以a1=1,因此an=3n-1(n∈N*).

(3)下面分三种情况进行证明:

①若D⊆C,则SC+SC∩D=SC+SD≥SD+SD=2SD.

②若C⊆D,则SC+SC∩D=SC+SC=2SC≥2SD.

E≠∅,F≠∅,E∩F=∅，

从而SC=SE+SC∩D,SD=SF+SC∩D,由SC≥SD,可得SE≥SF.

设k为E中的最大数,m为F中的最大数,则k≥m,m≥1,k≠m.由(2)可得SE

SF≤a1+a2+…+am

=1+3+…+3m-1

所以SE≥2SF+1,

整理,可得SC+SC∩D≥2SD+1.

综合①②③,可得SC+SC∩D≥2SD.

评注这是一道数列创新题,解决此题的关键就在于对新运算的理解与运用.第(1)问利用新定义和等比数列的通项公式求解;第(2) 问利用等比数列的求和公式,并结合放缩法使问题得以顺利证明;第(3)问合理利用化归与转化思想以及分类讨论思想,并结合推理知识，问题即可得证.

三、新数列性质创新题

例4(上海卷)若无穷数列{an}满足:只要ap=aq(p,q∈N*),必有ap+1=aq+1,则称{an}具有性质P.

(1)若{an}具有性质P.且a1=1,a2=2,a4=3,a5=2,a6+a7+a8=21,求a3;

(2)若无穷数列{bn}是等差数列,无穷数列{cn}是公比为正数的等比数列,b1=c5=1,b5=c1=81,an=bn+cn,判断{an}是否具有性质P,并说明理由;

(3)设{bn}是无穷数列,已知an+1=bn+sin an(n∈N*),求证:“对任意a1,{an}都具有性质P”的充要条件为“{bn}是常数列”.

解(1)由题意,可知a2=a5=2,从而a3=a6,a4=a7=3,a5=a8=2.

由a6+a7+a8=21,可得a6=21-a7-a8=21-3-2=16,即a3=16.

(2)设{bn}的公差为d,{cn}的公比为q(q>0),则b5-b1=4d=80,从而d=20,所以bn=b1+(n-1)d=20n-19.

故{an}不具有性质P.

(3)充分性:若数列{bn}为常数列,令bn=C(其中C为常数),则

an+1=C+sin an(n∈N*).

若存在p,q使得ap=aq(p,q∈N*),则

ap+1=C+sin ap=C+sin aq=aq+1,

即ap+1=aq+1，故{an}具有性质P.

必要性：若对任意a1,{an}都具有性质P,则a2=b1+sin a1.

令函数f(x)=x-b1,g(x)=sin x,则对任意的b1,函数f(x)与g(x)的图象必有一个交点,即存在a1,使得f(a1)=g(a1),即a1-b1=sin a1,从而a1=b1+sin a1=a2,an=an+1,从而bn+1=an+2-sin an+1=an+1-sin an=bn.

故数列{bn}是常数列.

综上可知,“对任意a1,{an}都具有性质P”的充要条件为“{bn}是常数列”.

评注本题是数列的新定义性质创新试题,解决此题的关键就在于对新定义数列性质的正确理解与灵活运用.

四、数列综合型创新题

例5(北京卷)设数列A:a1,a2,…,aN(N≥2)，如果对小于n(2≤n≤N)的每个正整数k都有ak

(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;

(2)证明:若数列A中存在an使得an>a1,则G(A)≠∅;

(3)证明:若数列A满足an-an-1≤1(n=2,3,…,N),则G(A)的元素个数不小于aN-a1.

解(1)易求G(A)的所有元素为2与5.

(3)当aN≤a1时结论成立.

以下设aN>a1,由(2)可知G(A)≠∅.

设G(A)={n1,n2,…,np},且n1

an0

对i=0,1,…,p,记

若Gi≠∅,取mi=minGi,则对任意1≤k

故G(A)的元素个数p不小于aN-a1.

评注这是一道集合与数列的综合创新试题，主要考查新定义数列、集合以及不等式等基础知识.而解题的关键就在于对新定义数列的理解与运用,同时也考查化归与转化数学思想、运算求解能力以及创新意识.

综上可知,对已有的知识进行创新,已成为近几年高考数学卷的一大亮点.这就要求学生面对生疏情境,能迅速从问题中提取有用信息,进而对这些有用信息进行加工,合理迁移，运用已学的知识加以解决.这里有用信息的提取以及化归与转化是解题的关键,同时也是解题的一个难点.由于创新试题能够较好地考查学生的知识迁移能力与转化能力,从而可检测学生理性思维的广度与深度以及继续学习的潜能,因此,在平时的学习过程中应予以高度重视.