导数在高中数学教学中的应用
◇ 山东 杜保华
导数在高中数学教学中的应用
◇山东杜保华
导数在高中数学教学大纲中占有很重要的位置,其应用主要有以下3个方面:求曲线的切线、判断函数的单调性、求函数的极值.下面,笔者将结合自身多年来导数的教学经验,就导数在这3个方面的应用举例说明.
1 用导数求曲线的切线
一个函数在某一点的切线斜率就是该点的导数值.例如:求函数y=x2+x在点A(a,b)的切线斜率.首先,对函数进行一阶求导,得y′=2x+1,再将点A横坐标代入就可以得到切线斜率k=2a+1.
导数的本质是通过极限的概念对函数进行局部的线性逼近,例如,北京大学出版社出版的高中数学课本第3章第1节有例1这样的一道习题.


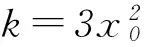
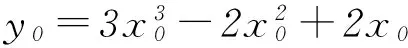
最后,将点A坐标代入曲线C的方程中就可以求出x0和y0的值,也就可以求出k的值及直线l的方程式.
2 用导数判断函数的单调性
利用某个函数导数的正负,可以判断该函数在某一区间是单调递增还是单调递减.
例如,设函数f(x)在R内存在某个独立的区间(a,b),如果f(x)的导数f′(x)在区间内(a,b)的值恒大于0,则函数f(x)在区间(a,b)内单调递增;如果f′(x)在区间(a,b)内的值恒小于或等于0,则函数f(x)在区间(a,b)内单调递减.
相应地可以证明,当函数f(x)在区间(a,b)内单调递增,则说明f′(x)的值在此区间内恒大于或等于0;当函数f(x)在区间(a,b)内单调递减,则f′(x)的值在此区间内恒小于或等于0.
在判断某个函数的单调区间时,要先求出该函数的导数f′(x),再用f′(x)=0的根将f(x)的定义域分成若干区间,列表考查此区间内f′(x)的符号,进而确定f(x)的单调区间.
注意,并不是所有的函数都有导数,也存在许多不可导的函数,例如:函数y=|x|,当x=0时,该函数是不可导的.一个函数不一定在所有的点上都有导数,若某函数在某一点有导数存在,则称该函数在这一点可导,否则称该函数在这一点不可导.并且,可导的函数一定连续;不连续的函数一定不可导.另外,还要谨记,如果一个函数是某个常数,则该函数的导数等于零.


1) 当a<0时,方程g(x)=ax2+2ax-1=0的判别式为Δ=4a2+4a,令Δ=0,解得a=0(舍去)或a=-1.
2) 当a=-1时,g(x)=-x2-2x-1=-(x+1)2≤0,即f′(x)=(ax2+2ax-1)·ex≤0,且f′(x)在x=-1两侧同号,仅在x=-1时等于0,则f(x)在(-∞,+∞)上为单调减函数.
3) 当-1 2ax-1<0恒成立,即f′(x)<0恒成立,则f(x)在 (-∞,+∞)上为单调减函数. 4) 当a<-1时,Δ=4a2+4a>0,令g(x)=0,方程ax2+2ax-1=0有2个不相等的实数根 如果函数f(x)的导数f′(x)在某一点的值0,则该点称为函数f(x)的驻点(也可能是该函数的极值点),进一步判断是极大值还是极小值则需要对该点左、右两侧的导数值进行判断.例如,若函数f(x)的导数f′(x)在x=x0的导数值为0,在临近x0的左侧,f′(x)<0,在临近x0的右侧,f′(x)>0,则x=x0称为函数f(x)的极小值点. 同理,若在临近x0的左侧,f′(x)>0,在临近x0的右方,f′(x)<0,则x=x0称为函数f(x)的极大值点;若在临近x0的左侧和右侧,f′(x)均大于零或者均小于0,则x=x0称为函数f(x)的驻点,也就是说,x=x0既不是函数f(x)的极大值点,也不是函数f(x)的极小值点. (1) 求f(x)的单调区间. 大数据的利用主体是人,人们有必要变革其中的不合理及其消极因素,并将网络伦理道德内化为大数据开发者、创新者以及作为使用者的草根阶层本身的意识。无论大数据技术多么强大,至关重要的是在网络空间中传承卓越的人类的善和道德价值,它们是实现人类繁荣的基础。网络空间的终极管理者是道德价值而不是工程师的代码。[11]也就是说,在网络空间中诉诸道德,而非大数据技术来实现网络草根民主更具有合理性。 (2) 是否存在实数k,使得函数f(x)的极大值等于3e-2?若存在,求出k的值;若不存,请说明理由. e-kx(2x+1)=e-kx[-kx2+(2-k)x+2], 即 f′(x)=-e-kx(kx-2)(x+1) (k<0). 当k=-2时,f′(x)=2e2x(x+1)2≥0,故f(x)的单调递增区间是(-∞,+∞); 当-2 表1 当k<-2时,f(x)、f′(x)随x的变化情况见表2. 表2 (2) 当k=-1时,f(x)的极大值等于3e-2. 理由如下: 当k=-2时,f(x)无极大值. 当-2 综上所述,当k=-1时,f(x)的极大值等于3e-2. 下面,笔者将求函数极值的方法进行简单总结. 求可导函数极值的步骤: 1)确定函数定义域,求函数的导数f′(x); 2)求出满足f′(x)=0的所有实数根; 3)对每个实数根进行检验,判断在每个根(如x0)的左、右两侧导函数f′(x)的符号如何变化. 通过笔者对导数的应用分析,不难看出,导数对函数问题的解决十分重要.根据笔者对各省市近几年数学高考卷的题型统计发现,对导数应用的考查越来越频繁,渐渐变成了命题的热点.熟练地运用导数不仅可以更迅速、准确地解题,还能开拓学生在解题时的思维方式,培养创新的思维习惯;因此,在平时的解题教学中应加强对导数内容的学习与巩固. 山东省枣庄市第八中学 )
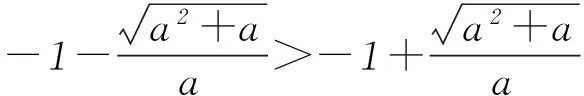

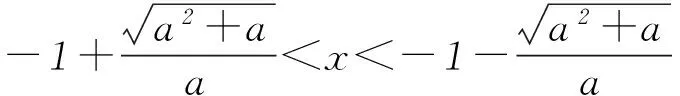
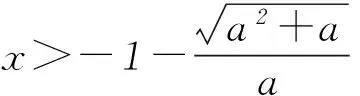
3 用导数求函数的极值