横向探究均值不等式的交汇

☉江苏省张家港市沙洲中学　陈燕

横向探究均值不等式的交汇

☉江苏省张家港市沙洲中学陈燕

均值不等式是高考重点考查内容，其主要用于求函数最值，其二元形式是a+b≥0），当且仅当a=b时，取“=”.常考的变形形式a2+b2≥2ab，当a=b时，取“=”.另外还可以推广到“三元”或“多元”的形式，应用中注意其适用条件.在知识综合交汇处命题，能有效考查同学们综合应用所学知识解决问题的能力，因此备受命题人关注.下面就均值不等式的交汇考查视角，举例分析.

一、与向量交汇，展示向量数的特征

A．13B．15C．19D．21

点评：向量具有代数和几何双重身份，通过代数化后，向量的最值问题就转化为函数最值问题，进而再借助均值不等式求最值.在向量代数化过程中向量的几何运算，即加法三角形法则、平行四边形法则，减法的三角形法则起着关键的作用.运用这些法则可实现未知向量向已知向量的转化.

二、与数列交汇，体现数列放缩技巧

例2（2015年陕西）设fn（x）是等比数列1，x，x2，…，xn的各项和，其中x＞0，n∈N，n≥2.

（Ⅰ）证明：函数Fn（x）=fn（x）-2在）内有且仅有一个零点（记为xn），且

（Ⅱ）设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为gn（x），比较fn（x）与gn（x）的大小，并加以证明.

解析：（Ⅰ）证明：因为Fn（x）=fn（x）-2=所以函数Fn（x）= fn（x）-2在函数Fn（x）=fn（x）-2在）内有且仅有一个零点（记为xn），又Fn（xn）=0，从而上为增函数，并且Fn（1）=n-1＞0，，所以

（Ⅱ）由题意，设｛an｝，｛bn｝分别是满足条件的等差数列和等比数列，｛an｝的公差为d，则an=1+（n-1）d，bn=xn-1且 xn=1+nd，即d=

若x=1，则an=bn，所以fn（x）=gn（x）；

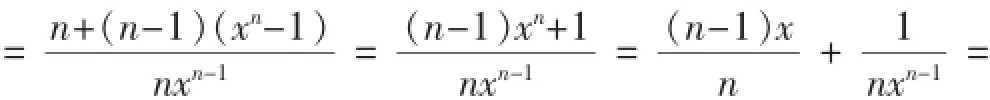
综上所述，当x=1时，fn（x）=gn（x）；当x＞0且x≠1时，fn（x）＜gn（x）.

点评：利用基本不等式，是处理含根式问题的常见方法，在高考中有广泛应用.通过用基本不等式进行放缩后，转化为我们常见的裂项放缩求和.例2证明中运用了基本不等式a+b≥2的推广形式a1+a2+a3+…+an≥（其中an＞0，n∈N*）进行放缩.

三、与三角交汇，探究三角边角关系

例3设△ABC的内角A，B，C所对边的长分别为a，b，c，则下列命题正确的是________（写出所有正确命题的编号）.

①若ab＞c2，则C＜；②若a+b＞2c，则C＜③若a3+ b3=c3，则C＜若（a+b）c＜2ab，则C＞⑤若（a2+ b2）c2＜2a2b2，则C

解析：①由ab＞c2，得-c2＞-ab，由余弦定理可知，cosC=，因为C∈（0，π），函数y=cosx在（0，π）上是减函数，所以C＜，即①正确.

③若C是直角或钝角，则a2+b2≤c2，即∈（0，1），而函数y=ax（0＜a＜1）在R上是减函数，所以）2≤1与a3+b3=c3矛盾，所以假设不成立，所以C＜即③正确.

⑤因为（a2+b2）c2＜2a2b2，所以c2＜ab＞c2，转化为命题①，故⑤错误.

答案：①②③.

点评：均值不等式与解三角形的交汇，最直接的体现是与余弦定理的交汇，从余弦定理的形式上看，具有边的二次方形式，因为其与均值不等式的交汇非常自然.

四、与圆锥曲线交汇，尽显解析几何代数性

（Ⅰ）求椭圆C的方程.

（Ⅱ）在椭圆C上，是否存在点M（m，n），使得直线l：mx+ny=1与圆O：x2+y2=1相交于不同的两点A，B，且△ABO的面积最大？若存在，求出点M的坐标及对应的△ABO的面积；若不存在，请说明理由.

设P（x，y）为椭圆C上任意给定的一点，|PQ|2=x2+（y-2）2=-2（y+1）2+6+3b2≤6+3b2，y∈［-b，b］.

由题设存在点P1满足|P1Q|=3，则9=|P1Q|2≤6+3b2，所以b≥1.

当b≥1时，由于y=-1∈［-b，b］，此时|PQ|2取得最大值6+3b2.所以6+3b2=9⇒b2=1，a2=3.故所求椭圆C的方程为

（Ⅱ）存在点M满足要求，使△ABC的面积最大.

假设直线l：mx+ny=1与圆O：x2+y2=1相交于不同的两点A，B，则圆心O到l的距离d=

因为|AB|=2，所以S△OAB=

当且仅当1-时等号成立.所以满足

点评：几何问题代数化是处理解析几何问题的常用策略，解题中既可以将几何问题直接代数化，也可以先把几何问题利用几何方法进行适度简化，再代数化.通常前者思维量小但计算量大；后者计算量小但思维量大.代数化后几何最值问题就转化为函数最值，再结合均值不等式即可求解.

均值定理是高中数学中重要的内容，在高考中占有很重要的地位，成为高考的高频考点.在近年高考命题中，对均值不等式的考查多与其他知识相交会，体现高考命题能力立意的理念，成为检查学生知识综合掌握情况和提升学生应用能力的训练战场.Y