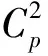内交换p群的非正规子群的共轭类数

张慧玲，白 颉

(太原学院 数学系， 太原 030001)



内交换p群的非正规子群的共轭类数

张慧玲*，白 颉

(太原学院 数学系， 太原 030001)

研究有限群的非正规子群的共轭类数是群论学中的一个重要课题.下面借助于内交换p群的分类，对内交换p群的非正规子群的共轭类数进行讨论，给出了ν(G)=p、ν(G)=p+1和ν(G)=p+2时内交换p群的分类．

内交换p群； 非正规子群； 共轭类数

正规子群在研究群的结构中起着重要作用，具有“较多”正规子群的有限群的研究一直是群论学中的一个重要研究内容，换句话说，研究具有“较少”非正规子群的有限群的结构成为群论学中的一个重要研究方向.ν(G)这个符号是由R.Brandl于1995年在文[3]中首次引入，它表示有限群G的非正规子群的共轭类数.显然，Dedekind群恰为ν(G)=0的有限群.文[3]决定了ν(G)=1的有限群，文[4]给出了ν(G)=1的有限p群的分类，文[5]给出了ν(G)=2的有限幂零群的分类，文[6]决定了ν(G)=2的有限群，文[7]又分类了ν(G)=3的有限p群.由于ν(G)=1、ν(G)=2和ν(G)=3的有限p群均已分类，很自然地，分类ν(G)较小的有限p群成为人们关心的一个问题.下面借助于文[1]内交换p群的分类，对内交换p群的非正规子群的共轭类数进行讨论，给出ν(G)=p、ν(G)=p+1和ν(G)=p+2时内交换p群的分类.

引理1 ([1]，第70页，定理2.3.7)设G是内交换p群，则G是下列互不同构的群之一：(1)Q8；

(2)Mp(n，m)=〈a，b|apn=bpm=1，ab=a1+pn-1〉，n≥2，m≥1，(亚循环情形)；

引理2([1]，第53页，命题2.1.2)设G是幂零类为2的群，x，y，z∈G，则

[x，yz]=[x，y][x，z];

(2)[xn，y]=[x，y]n=[x，yn];

引理3([2]，第1098页，定理1)设G是有限p群，则ν(G)=2当且仅当G同构于下列群之一：(1)M2(n，2)，其中n≥2；(2)D8；(3)Q16．

引理4 ([4]，定理59.1)设G是有限p群，若G的所有非正规子群都共轭，则G≅ Mp(n，1)，若p=2，则n≥3．

为了讨论内交换p群的非正规子群的共轭类数，首先给出3个命题：

证明结论是显然的．

命题2设G是亚循环的内交换p群，若H

命题3设G是非亚循环的内交换p群，若H

定理1设G是亚循环的内交换p群，G≅Mp(n，m)， n≥2，m≥1，

(2)若2≤n

证明(1)首先可证G中除pm阶子群外，其他子群均正规：

ii.所有pm阶非正规子群只有形式〈balpn-m〉且0≤l≤pm-1:

下面分两种情形对pm阶元bkal′pn-m中的k讨论.

再证ν(G)=pn-1+(m-n)(pn-1-pn-2)：

下证上述所得的非正规子群随着参数的不同而不同.

i. 〈bai〉随着i的不同而不同，其中1≤i≤pn：

若否，存在1≤i1，i2≤pn，i1≠i2，使得〈bai1〉=〈bai2〉成立，于是不妨设bai1=bai2，于是ai1-i2=1，进而i1=i2，矛盾．

ii. 〈bpm-kai〉随着i，k的不同而不同，其中1≤i≤pn且(i，p)=1：

若否，存在1≤i1，i2≤pn，i1≠i2n≤k1，k2

因此对于(2)，群G共有pn+(m-n)(pn-pn-1)个非正规子群，再由命题1知，每个非正规子群的共轭类长度为p，故ν(G)= pn-1+(m-n)(pn-1-pn-2)．

定理2设G是非亚循环的内交换p群，G≅Mp(n，m，1)，n≥m，当p=2时，m+n≥3，

(1)若n=1，则ν(G)=p+1；

(2)若n≥2，则ν(G)≥2p+1>p+2．

证明(1)由Mp(1，1，1)为p3阶非交换群，知其非正规子群只能为p阶子群.又G是极小非正规子群，于是只有1个p阶正规子群，即为G′，其余的p阶子群均不正规.又由于Mp(1，1，1)共有p2+p+1个p阶子群，于是有p2+p个非正规子群，于是由命题1知ν(G)=p+1．

(2)只需证G中至少存在2p+1个互不共轭的非正规子群即可．

下证子群〈baipn-m〉，〈bjpa〉和〈apsct〉×〈b〉为G的互不共轭的非正规子群，其中i=1，2，…，pm；j=1，2，…，pm-1；s=1，2，…，n-1；t=0，1，…，p-1．

首先易知子群〈baipn-m〉、〈bjpa〉和〈apsct〉×〈b〉之间不共轭且均不正规，下证〈baipn-m〉和〈bjpa〉之间互不共轭：若否，只能有m=n，于是存在bj′ai′ck′∈G使得 (bai)bj′ai′ck′=baic-i′cij′∈〈bjpa〉，于是存在s′满足(s′，p)=1使得baic-i′cij′=(bjpa)s′=bjs′pas′成立，即b1-js′p=as′-ici′-ij′，由(1-js′p，p)=1且〈a〉×〈c〉∩〈b〉=1知矛盾．

下证子群〈baipn-m〉随着参数的不同所对应的群也互不共轭，即证〈bai1pn-m〉和〈bai2pn-m〉不共轭，其中i1≠i2.

同法可证子群〈bjpa〉和〈apsct〉×〈b〉随着参数的不同所对应的群也互不共轭，因此得ν(G)≥pm+pm-1+(n-1)p≥p+1+p=2p+1>p+2．

由于ν(Q8)=0，自此内交换p群的非正规子群的共轭类数已讨论完毕，作为上述定理的应用，结合引理3和引理4，下面的定理3分别给出了ν(G)=p、ν(G)=p+1和ν(G)=p+2时内交换p群的分类：

定理3设G为内交换p群，

(1)若ν(G)=p，则G为下列群之一：D8，Mp(n，2)，其中n≥2；

(2)若ν(G)=p+1，则G为下列群之一：M2(2，3)，Mp(1，1，1)，其中p≠2；

(3)若ν(G)=p+2，则

当p=2时，G为下列群之一：M2(2，4)，M2(n，3)，其中n≥3；

当p=3时，G≅M3(2，3)；

当p≥5时，这样的群G不存在．

由以上3个定理及引理4，还可推得下面的结论：

推论设G为内交换p群，则ν(G)=1，或者ν(G)≥p．

[1] 徐明耀， 曲海鹏. 有限p-群[M].北京：北京大学出版社，2010．

[2] 陈贵云， 陈顺民. 非正规子群的共轭类数为2的有限群的一个注记[J].吉林大学学报，2008， 46(6)：1097-1100．

[3] BRANDL R. Groups with few non-normal subgroups[J].Comm.Alg，1995， 23 (6)：2091-2098．

[4] SCHMIDIT O Y.Groups having only one class of non-normal subgroups(Russian)[J] .Mat Sb， 1926， 33:161-172．[5] SCHMIDIT O Y.Groups with two classes of non-normal subgroups(Russian) [J].Proc Seminar on Group Theory， 1938， 33:7-26．

[6] MOUSAVI H.On finite groups with few non-normal subgroups[J].Comm.Alg， 1999， 27 (7)：2091-2098．

[7] MOUSAVI H.Finite nilpotent groups with three conjugacy classes of non-normal subgroups[J]. Bulletin of the Iranian Mathematical Society, 2014, 40(5):1291-1300.

[8] ZHANG Q H， GUO X Q， QU H P， et al.Finite group which have many normal subgroups[J].J Korean Math Soc， 2009， 46 (6)：1165-1178．

The conjugacy classes of non-normal subgroups of internal exchangep-group

ZHANG Huiling, BAI Jie

(Department of Mathematics, Education Institute of Taiyuan University, Taiyuan 030001)

Study on the conjugacy classes of non-normal subgroups of finite groups is an important project in group theory. With the classification of internal exchangep-group, the conjugacy classes of non-normal subgroups are discussed, and the classification of internal exchangep-group whenv(G)=p,v(G)=p+1 andv(G)=p+2 are given.

internal exchangep-group; non-normal subgroups; conjugacy class

2016-03-09.

国家自然科学基金项目(71561008).

1000-1190(2016)04-0486-03

O152.1

A

*E-mail: huiling.103020@163.com.