一种三维线弹性随机数值均化方法

王 南,马 娟,张玉林

(西安电子科技大学机电工程学院,陕西西安 710071)

一种三维线弹性随机数值均化方法

王 南,马 娟,张玉林

(西安电子科技大学机电工程学院,陕西西安 710071)

对小变形下具有随机微观结构非均质材料的数值均化问题进行了研究.当考虑材料微观结构形态、各组分性质的随机性及相关性时,基于多尺度有限元方法和蒙特卡罗法,建立了非均质材料的随机均化模型.求出了不同边界条件下的随机有效量及其数字特征值以及有效量之间所具有的相关性.考察了随机微观结构参数对随机有效量以及表征体积单元中应力分布的影响.结果表明,在分析非均质材料的宏观有效力学性质时,考虑材料微观结构中客观存在的随机性和相关性非常重要.

均化;随机性和相关性;三维线弹性;有限元法;蒙特卡罗法

非均质材料在持续的机械应力和热应力的作用下,其微观特性对材料整体性能[1]有着至关重要的影响.就非均质材料而言,均化方法作为一种将材料微观特性和宏观响应联系起来的有效方法已经发展了数十年.用均化方法得到的等效性质可以把宏观的非均质材料转化为等效的均值材料,而且极大地减少了求解时需要的自由度的个数.此外,通过引入应用了功准则的有效特征,均化方法亦极大地减少了解决宏观问题所需的计算量.就线弹性非均质材料的均化而言,目前已发展的较为完善,其中解析均化法可参见文献[2],数值均化方法参见文献[3].就其实质而言,均化是通过确定和分析具有统计意义的非均质材料的表征体积单元(Representative Volume Element,RVE)[4],获得非均质材料弹性张量的估值或一组边界值.

非均质材料的重要特征之一是其成分材料、缺陷分布以及这些因素间的相互作用的不确定性.近年来,对材料参数和荷载不确定性[5]的认识使得随机非均质材料得到关注并取得了一些研究成果[6-8].文献[6]解决了多孔领域中障碍问题的均匀化,其中孔洞是周期分布且拥有随机的形状和尺寸.文献[7]基于高斯随机场的非线性转化重构了带有随机形态的两相复合材料,并按照给定的统计特征值提出了一种高效的计算方法.文献[8]采用广义变分原理将一个带有随机微观结构的边值问题分解为一个慢尺度的确定性问题和一个快尺度的随机问题.

尽管取得了一些进展,但对于非均质材料的随机均化分析仍有待进一步深入研究.由于该类问题需从非均质材料不同尺度上的不确定变量入手来求解,已有的随机均化方法主要是通过减少微观结构中随机变量的数目来达到简化的目的的,其大致可分为两类,一类是仅考虑微观结构形态的不确定性[5-10];另一类是直接采用组分的杨氏模量和泊松比,而不是采用多尺度有限元法从组分的体积模量和剪切模量进行推导得出[11].此外,已有的均化模型几乎均未涉及微观结构参数间的相关性和均化结果之间的相关性.而微观结构所具有的随机性和相关性是客观存在、不容回避的,故亟需发展充分考虑微观结构不确定性的随机均化分析模型,并建立非均质材料微观结构的不确定性与材料整体宏观性质不确定性之间的量化关系.

笔者对小变形下三维线弹性随机非均质材料的均化问题进行了研究.当同时考虑微观结构所具有的随机性及相关性时,基于多尺度有限元方法以及蒙特卡罗法构建了随机均化模型,并对不同边界条件下材料的随机有效量如有效模量、有效弹性参数和有效弹性张量及其数字特征值进行了求解;最后考察了微观结构的不确定性对随机均化结果的影响,得到了一些有意义的结论.

1　线弹性非均质材料的均化问题

1.1均化问题

设由均匀各向同性的基体(M1)和颗粒(M2)材料组成非均质材料M如图1所示,其参考形状为R0,本构方程σ=(X,ε),其中σ和ε分别表示应力和应变,X为表征R0位置的矢量.图1中,L表示介观,d表示微观,D表示宏观,且将宏观非均质材料用等效均质材料替代.

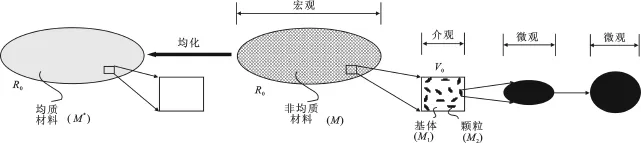
图1　二相非均质材料的均化问题及其微观-介观-宏观的尺度准则

关于该非均质材料M的一个力学边值问题为:求解位移u(X,t),以便下述方程在R0上成立:

其中,在∂Ru、∂Rt上的边界条件分别是:u=和t=σn=,ρ是材料的密度,ρb和ρ分别为宏观体力和惯性力.因M固有的非均质性所引起的求解困难,采用等效均质材料M*替代M后得到式(1)中x的近似解x*,故关于M*的均化问题成为:确定u*(X,t),以使式(2)在R0上成立:

其中,∂Ru、∂Rt上的边界条件分别是:u*=和t*=σ*n=,本构方程为σ*=*(X,ε*).

1.2有效本构关系

均化结果的准确性与材料的表征体积单元直接相关.考虑图1所示非均质材料中的一个表征体积单元,其体积为V0,即V0⊂R0.在微观结构分析中,忽略宏观体力和加速度,且边界条件服从Hill功准则.若将表征体积单元进行有限元网格划分,则均化过程中需要求解的边值问题即简化为求解u(X),以便

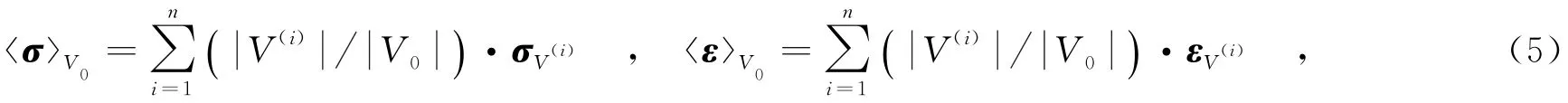
材料的有效弹性张量C*可由和计算得到[3]

1.3几类特殊的边界条件

在表征体积单元上施加的边界条件可分为由平均应力Σ控制的边界条件和由平均应变ε控制的边界条件,其中平均应力Σ为给定的常量,而平均应变ε=(〈H〉+〈H〉T)/2中平均位移梯度〈H〉是给定的常量.均化理论中4种广泛使用的由平均应变ε和平均应力Σ控制的边界条件[12]分别为:平均应变控制的线性位移边界条件(ε-Linear Displacement Boundary Conditions,ε-LD-BCs)、平均应变控制的周期性边界条件(ε-PeRiodic Boundary Conditions,ε-PR-BCs)、平均应变控制的均匀应力边界条件(ε-Uniform Traction Boundary Conditions,ε-UT-BCs)和平均应力控制的均匀应力边界条件(Σ-UT-BCs).

欲求解C*,可通过在表征体积单元上施加边界条件并通过体积平均获得其有效应力后按式(6)获得.

1.4基于有限元法的宏观有效量

此外,将边界条件施加于表征体积单元得到有效应力σ*和有效应变ε*后,有效体积模量和有效剪切模量分别为

其中,有效应力σ*和有效应变ε*是表征体积单元上的体积平均量和;张量A的(′)部分定义为A′=A-(tr(A)/3)I.

三维线弹性材料的有效杨氏模量E*和泊松比ν*可计算如下:

2　基于蒙特卡罗法的线弹性非均质材料的随机均化

考虑由两种均匀各向同性材料组成的二相非均质材料,即在基体中加入不同材质、随机分布的圆形颗粒.基体和颗粒的体积模量和剪切模量分别为k1、u1和k2、u2,颗粒体积比V2,半径为r.随机均化流程如图2所示.假设k1、 u1、k2、u2、V2和r为正态分布的随机变量:、u1～,其中μ和dmsd分别为变量的均值和均方差.k1、 u1和k2、u2的相关系数分别为和.利用蒙特卡罗法可生成各随机参数变量的m个样本,其中第j组样本为k1j、k2j、u1j、u2j、V2j和rj,且k1j、u1j和k2j、u2j是根据随机向量协方差矩阵的乔列斯基分解[13]并按照和产生的,故满足及

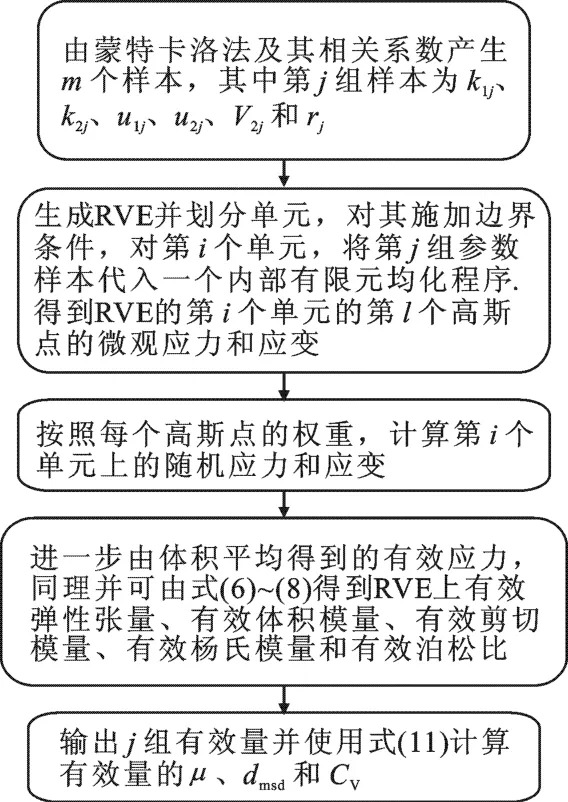
图2　随机均化流程图

用随机序列添加算法[14]生成表征体积单元并将其划分为n个单元后,对其施加边界条件.对第i个单元,将第j组参数样本代入一个内部有限元均化程序中,首先可获得第i个单元上第l个高斯点的随机微观应力和微观应变.之后按照每个高斯点的权重系数ωl可得到第i个单元上的随机应力,即

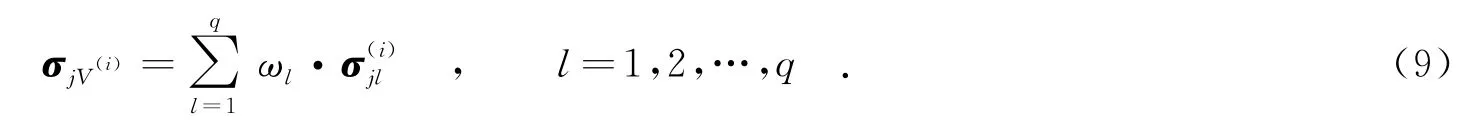
进一步由体积平均可得到表征体积单元上的随机有效应力为

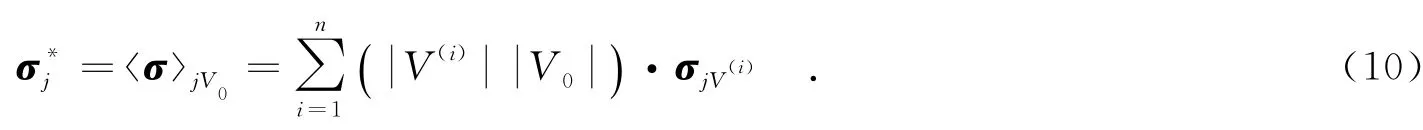
同理可由式(6)～(8)得到表征体积单元上的有效弹性张量、有效体积模量、有效剪切模量、有效杨氏模量和有效泊松比,将这些有效量统一用Q*表示.以此类推,m组参数样本代入程序后即获得m组有效量Q*.由数理统计即可求得有效量Q*的均值μ、均方差dmsd和变异系数CV为

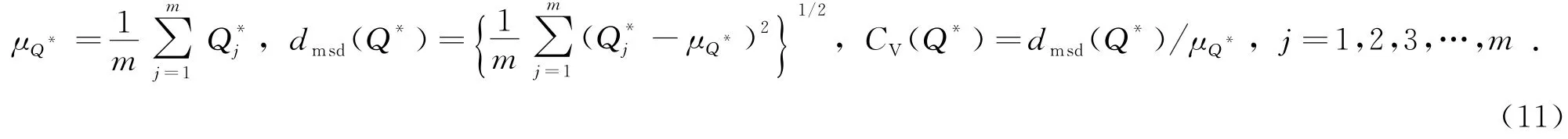
3　数值算例

针对一种颗粒随机分布的二相非均质材料,表1给出了基体及颗粒的各向同性材料参数的均值和变异系数,k1、u1和k2、u2之间的相关系数

表1　一种二相随机非均质材料的微观结构参数

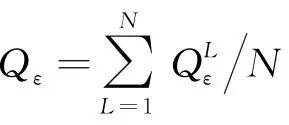
下面均化计算中所用的微观结构参数均为表1中的值,蒙特卡罗法模拟的次数为5000次.

表2是3种边界条件下求解获得的随机有效弹性参数E*和ν*.从表2可见,ν*的均方差随着V2的增大而增加,而E*的数字特征值和ν*的均值则相反;不同边界条件下ν*的均方差满足不等式(·)ε-LD-BCs＞(·)ε-PR-BCs＞(·)ε-UT-BCs;而E*的数字特征值和ν*的均值则满足不等式(·)ε-LD-BCs＜(·)ε-PR-BCs＜(·)ε-UT-BCs.图4则给出了±3dmsd原则下有效模量的取值范围,可见ρ=0.6时的取值范围大于ρ=0时的取值范围.从表2和图4可知,是否考虑参数间的相关性对均化结果是有影响的.

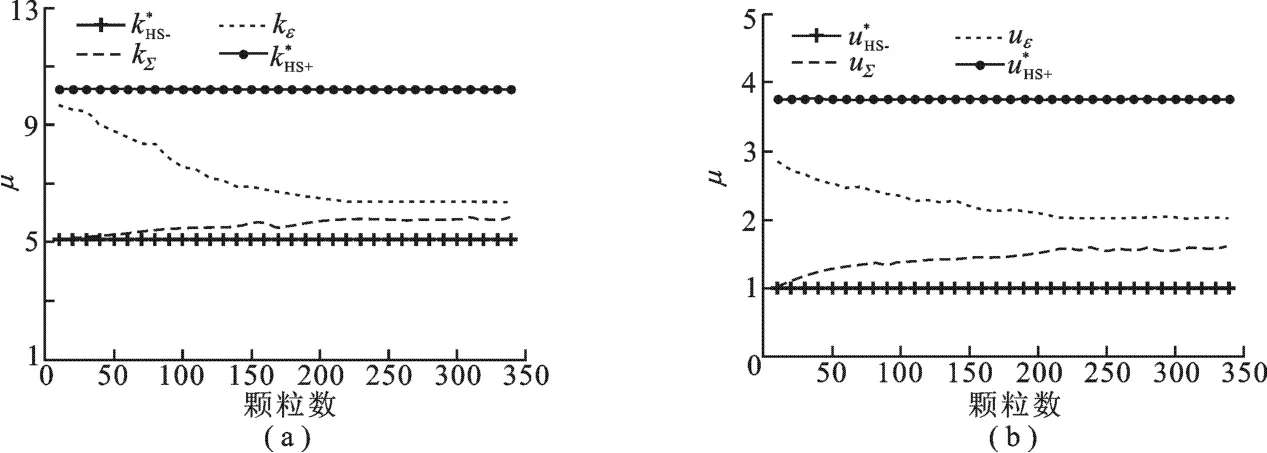
图3　非均质材料线弹性均化的解析解和数值解的均值比较

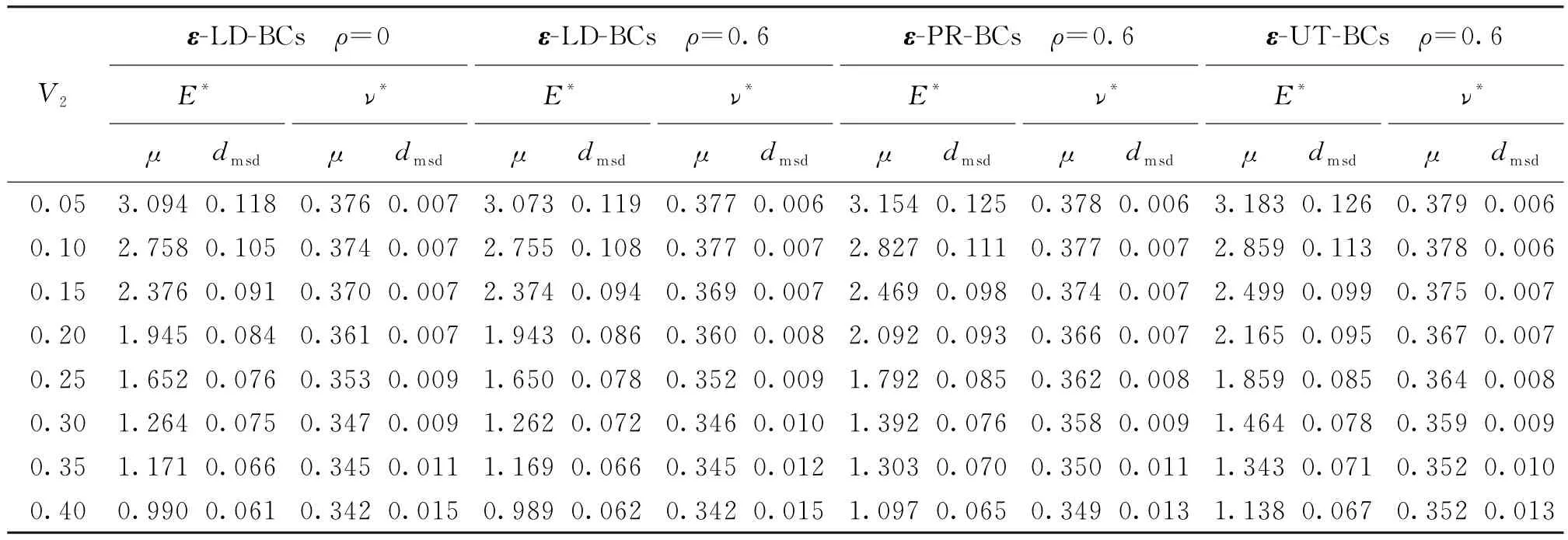
表2　随机有效弹性参数的均值和均方差

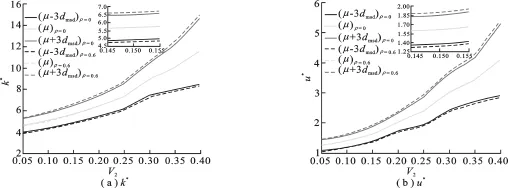
图4　ε-LD-BCs下两种相关情况时k*和u*的取值范围

有效弹性张量C*中部分元素的数字特征值列于表3中,明显可见其数字特征值随着V2的增加而增加.

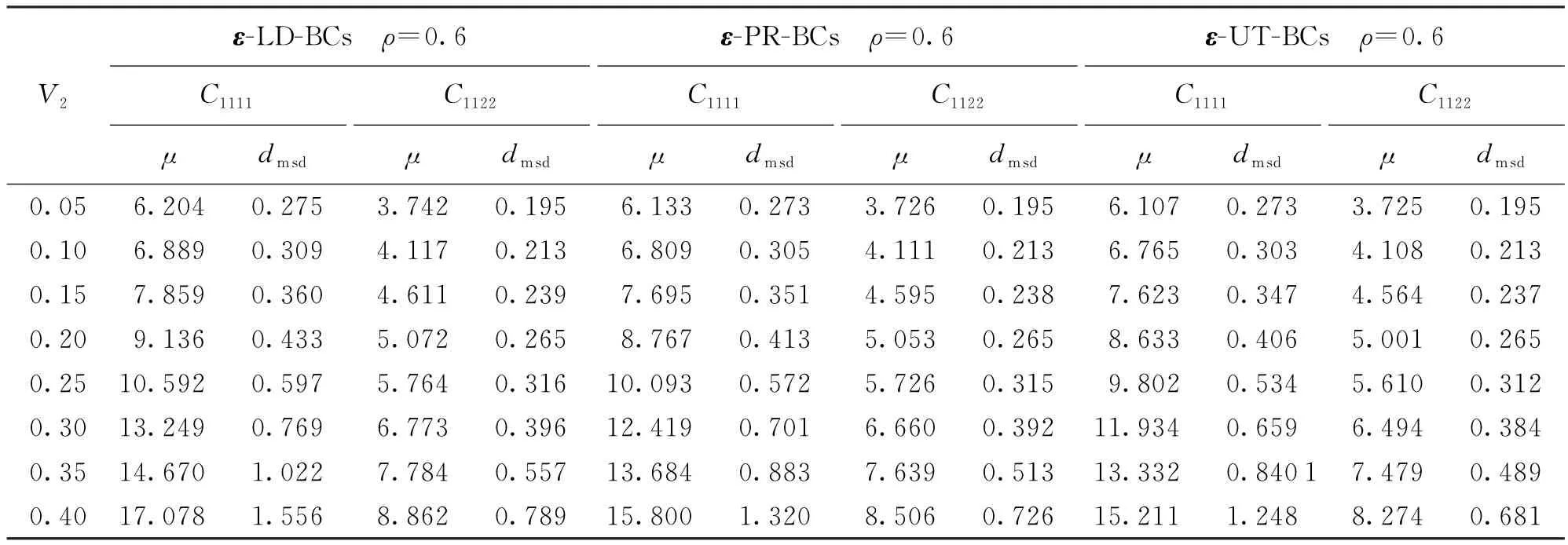
表3　有效弹性张量C*部分元素的数字特征值

当各随机参数的变异系数均为0.05时,考察了有效量间的相关性与随机参数间相关性的关系.由图5可知:随着随机参数间ρ的增加,k*和u*间的正相关性显著增强,而E*和ν*间的负相关性也随之增强.

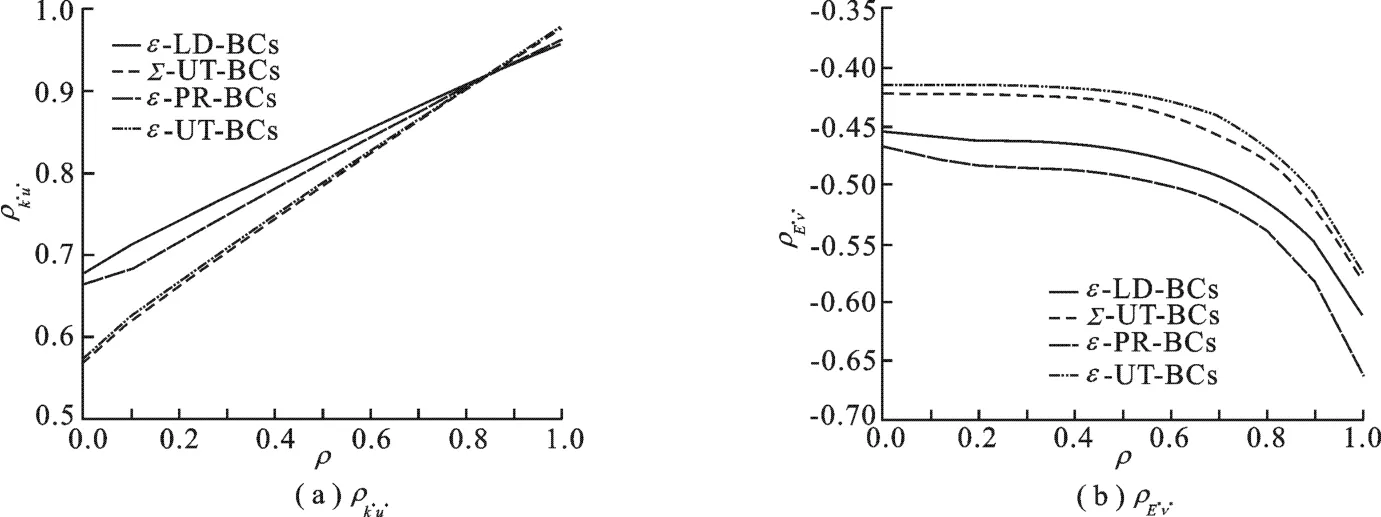
图5　当V2=0.25时和随变化的情况

图6　ρ=0.9时3种边界下表征体积单元中随机应力的分布图

从图6可见,在ε-PR-BCs下,表征体积单元的边界相对于ε-LD-BCs下的边界呈周期性变化,而ε-UT-BCs下表征体积单元边界的波动则无规律,这与各边界条件的本质密切相关;此外,不同的边界条件下应力分布的上界、均值和下界不相同;各图中应力分布均不均匀,离颗粒越近的基体中单元应力梯度越大且应力也越大,反之则越小.

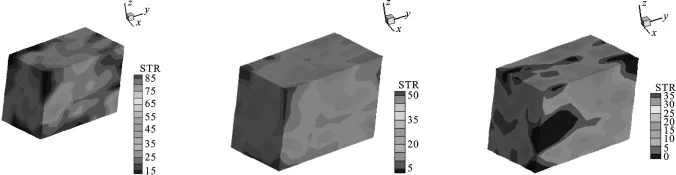
图7　ε-LD-BCs下,当ρ=0时表征体积单元中的随机应力分布图

图7为ε-LD-BCs下,各成分模量相互独立时表征体积单元中的随机应力分布图.与图6中第1行图形比较可见,两种相关情况下应力分布的上下边界明显不同,这是因为本质上两种相关条件下求得的有效模量、有效弹性参数和有效弹性张量是不同的.故在非均质材料有效力学性质分析或在进行含有非均质材料且承受静动态载荷的结构响应分析时,需要慎重考虑材料微观结构中客观存在的随机性和相关性.

4　结束语

笔者提出了一种多尺度随机均化方法来量化随机微观结构对材料随机有效量的影响,通过多尺度有限元法和蒙特卡罗法解决了小变形下三维线弹性材料的随机均化问题.数值算例采用二相非均质材料,当施加不同边界条件时求解了各随机有效量的数字特征如均方差、变异系数和相关系数等,并得出了一些有意义的结论.显然,随机数值均化模型是基于蒙特卡罗法发展而来的,因此其计算效率和结果的精确性与模拟次数直接相关.此外,也亟需采用其它随机方法来解决随机数值均化问题,从而使得两种方法的结果可以相互验证.三维数值算例表明:已建立的随机多尺度方法在有效评估及优化新材料、新结构方面具有潜在的应用价值;为更准确预测失效概率,概率高阶矩量信息和统计数据的获取也非常重要,相关研究也在进行.

[1]BRUNO D,GRECO F,LUCIANO R,et al.Nonlinear Homogenized Properties of Defected Composite Materials[J]. Computers&Structures,2014,134:102-111.

[2]NEMAT-NASSER S,HORI M.Micromechanics:Overall Properties of Heterogeneous Materials[M].2nd.Amsterdam: North-Holland,1999:27-71.

[3]ZOHDI T I,WRIGGERS P.Introduction to Computational Micromechanics[M].Berlin:Springer Verlag,2005: 63-104.

[4]NGUYEN V P,LLOBERAS-VALLS O,STROEVEN M,et al.Homogenization-based Multiscale Crack Modelling: from Micro-diffusive Damage to Macro-cracks[J].Computer Methods in Applied Mechanics and Engineering,2011,200 (9-12):1220-1236.

[5]MA J,TEMIZER I,WRIGGERS P.Uncertain Analysis of the Homogenization in the Heterogeneous Material of Linear Elasticity[J].International Journal of Solids and Structures,2011,48:280-291.

[6]CAFFARELLI L A,MELLET A.Random Homogenization of an Obstacle Problem[J].Annales de l’Institut Henri Poincare(C)Non Linear Analysis,2009,26(2):375-395.

[7]FENG J W,LI C F,CEN S,et al.Statistical Reconstruction of Two-phase Random Media[J].Computers& Structures,2013,137:78-92.

[8]XU X F,CHEN X.Stochastic Homogenization of Random Elastic Multi-phase Composites and Size Quantification of Representative Volume Element[J].Mechanics of Materials,2009,41(2):174-186.

[9]LE GUENNEC Y,COTTEREAU R,CLOUTEAU D,et al.A Coupling Method for Stochastic Continuum Models at Different Scales[J].Probabilistic Engineering Mechanics,2014,37:138-147.

[10]SAKATA S,ASHIDA F,OHSUMIMOTO K.Stochastic Homogenization Analysis of a Porous Material with the Perturbation Method Considering a Microscopic Geometrical Random Variation[J].International Journal of Mechanical Sciences,2013,77:145-154.

[11]SAKATA S,ASHIDA F,FUJIWARA K.A Stochastic Homogenization Analysis for a Thermoelastic Problem of a Unidirectional Fiber-reinforced Composite Material with the Homogenization Theory[J].Journal of Thermal Stresses, 2013,36(5):405-425.

[12]HILL R,RICE J R.Elastic Potentials and the Structure of Inelastic Constitutive Laws[J].SIAM Journal on Applied Mathematics,1973,25(3):448-461.

[13]TOURAN A,WISER E P.Monte Carlo Technique with Correlated Random Variables[J].Journal of Construction Engineering and Management,1992,118(2):258-272.

[14]JIA X,WILLIAMS R A.A Packing Algorithm for Particles of Arbitrary Shapes[J].Powder Technology,2001,120 (3):175-186.

[15]TEMIZER I,ZOHDI T I.A Numerical Method for Homogenization in Non-linear Elasticity[J].Computational Mechanics,2007,40(2):281-298.

(编辑:王 瑞)

Random computational homogenization for three-dimensional linear elasticity

WANG Nan,MA Juan,ZHANG Yulin
(School of Mechano-electronic Engineering,Xidian Univ.,Xi’an 710071,China)

The computational homogenization of heterogeneous materials under infinitesimal deformation is addressed in the context of elasticity when the uncertainty in microstructure is fully considered.Based on the multi-scale finite element method and Monte-carlo method,the random homogenization model of heterogeneous materials is established when the randomness of microstructural morphology and of material properties of constituents as well as the correlation of material properties are accounted for simultaneously. The random effective quantities and their numerical characteristics as well as their correlations under different boundary conditions are then found.And the impacts of microstructural parameters on random effective quantities are also investigated and illustrated.Finally,the random stress distributions within a representative volume element under different boundary conditions are revealed as well.Obviously,it is necessary that the randomness and correlation existing in the microstructure should be fully considered during the solution of the effective mechanical properties of heterogeneous materials.

homogenization;randomness and correlation;three-dimensional linear elasticity;finite element method;Monte-Carlo method

TB33;O343.2

A

1001-2400(2016)04-0092-08

10.3969/j.issn.1001-2400.2016.04.017

2015-04-20 网络出版时间：2015-10-21

国家自然科学基金青年基金资助项目(11102143);西安电子科技大学留学回国人员择优资助项目(6450041101)

王 南(1990-),男,西安电子科技大学硕士研究生,E-mail:wangnan@stu.xidian.edu.cn.

网络出版地址：http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.034.html