求解大规模线性离散不适定问题的RRArnoldi-Fractional Tikhonov正则化算法

张 慧

(南京航空航天大学 金城学院 基础部，南京 211156)



求解大规模线性离散不适定问题的RRArnoldi-Fractional Tikhonov正则化算法

张 慧

(南京航空航天大学 金城学院 基础部，南京 211156)

不适定问题广泛出现在地球物理、自动控制等多种领域.正则化方法是求解此类问题近似解的有效算法.将Fractional Tikhonov正则化算法应用于投影算法，提出了求解大规模线性离散不适定问题的Arnoldi-Fractional Tikhonov正则化算法.进一步提出限制值域的Arnoldi-Fractional Tikhonov正则化算法.并针对经典算例，进行了数值试验和比较.数值试验结果表明了新算法是有效且具有优势的.

不适定问题；正则化方法；Fractional正则化方法；Fractional Tikhonov正则化算法

随着科技日新月异的发展，不适定问题[1]广泛出现在图像恢复、数学物理等科学领域[2-3]，实际上，上述问题转化为线性离散不适定问题，即求解

Ax=btrue+e，A∈Rn×n

(1)

其中b=btrue+e是实际观测到的带有噪音的右端项，btrue是理想状态下的输出结果，e是观测过程中无法消除的噪音数据.而真正需要求解的线性系统为：

Axtrue=btrue，A∈Rn×n

(2)

因此，求解的难度就在于如何由已知的观测系统式(1)来求解未知的xtrue.

对于不适定问题求解的有意义研究开始于20世纪60年代，由前苏联A.N.Tikhonov[4]院士及其领导的工作小组在从事反问题理论研究中提出的，即当今最为著名和广为使用的Tikhonov正则化方法，它也一直是学者们研究的热点.2011年，Hochstenbach[5]和Reichel在此基础上进一步提出了Fractional Tikhonov正则化方法.本文在此基础上提出基于大规模系数矩阵A的投影Fractional Tikhonov正则化方法.

1 Fractional Tikhonov正则化方法

首先，考虑这样一个极小化问题：

(3)

其中α>0.若0<α<1，则矩阵W可以借助AAT的广义逆来表示.参数α的介入，会使得式(3)式的解xλ,α更接近线性系统式(1)的精确解.我们把上述方法称作Fractional Tikhonov正则化方法或Weighed Tikhonov正则化方法.在经典的Tikhonov正则化方法中α=1，即矩阵W=I.

为了求极小化问题(3)的解，我们可以转化为求解如下线性系统：

(4)

任意给定一个λ>0,α>0，就能求出一个正则解xλ,α，解的精确度与λ,α的选取息息相关.将系数矩阵A进行奇异值分解后即可转化为求解

(5)

其中

(6)

那么正则化解表示如下：

(7)

其中x=Vy.Fractional Tikhonov正则化方法的滤波因子为

(8)

假设已知右端输出项b中噪音部分e满足‖e‖≤ε，那么可以利用广义交叉准则确定正则化参数λ.令α>0，是事先定好的一个数值，定义

δ=ηε

(9)

这里取η>1，它是一个独立于ε的参量，第六部分的数值试验中均取η=1.1.要求正则化解xλ,α满足

‖b-Axλ,α‖2=‖δ‖2

(10)

将式(7)代入式(10)的左端，有

(11)

将式(8)代入式(10)右端(1-σjφtikh,W(σ))中，有

其中μ=λ-1，那么求解式(10)相当于求解下式的零点，

(12)

我们采用牛顿法求解上式，得到μ值进而确定λ值，代入式(8)求得正则化解.

2 Arnoldi Fractional Tikhonov 正则化方法

Fractional Tikhonov正则化方法建立在对系数矩阵A进行奇异值分解的基础上，然而对于大规模矩阵，它的奇异值分解需要非常大的计算量，因此我们选择先将大规模问题投影到维数较低的Krylov子空间上，对小规模问题进行求解.Lewis和Reichel在2008年提出Arnoldi Tikhonov方法[6]，详细地介绍了该类方法.

2.1 Arnoldi Tikhonov方法

1)选初始向量x0，计算残量r0=b-Ax0，β=‖r0‖,ν1=r0/‖r0‖;

2)for j=1,2,…,m

ωj=Aνj,

for i=1,2,…,j

hij=(ωj,νi),

ωj=ωj-hijνi,

end for

hj+1,j=‖ωj‖,

if hj+1,j=0

m=j，exit；

else

νj+1=wj/hj+1,j;

end if

end for

4)计算近似正则解xλ=x0+Vmyλ.

2.2 Arnoldi Fractional Tikhonov方法

1)选初始向量x0，计算残量r0=b-Ax0，β=‖r0‖,ν1=r0/‖r0‖;

2)for j=1,2,…,m

ωj=Aνj,

for i=1,2,…,j

hij=(ωj,νi),

ωj=ωj-hijνi,

end for

hj+1,j=‖ωj‖,

if hj+1,j=0

m=j，exit；

else

νj+1=wj/hj+1,j;

end if

end for

4)计算近似正则解xλ=x0+Vmyλ.

3 限制值域的Arnoldi Fractional Tikhonov正则化方法

Arnoldi类算法是建立在Krylov子空间span{b,Ab,A2b,…,Am-1b}的.这个子空间的最大缺点在于其包含了右端向量中的噪声成分，这意味着由b,Ab,A2b,…,Am-1b线性组合得到的解很有可能包含了大量的噪声成分.于是改进Krylov子空间如下

span{Ab,A2b,…,Amb}

这个子空间的优点在于，其噪声成分被乘上了矩阵A，而这样做，可以对噪声中的高频部分起到一种阻尼和光滑效果.这就是所谓的限制值域的Arnoldi类算法，记作RRArnoldi方法.

(13)

RRArnoldi算法简单描述如下：

3.1 RRArnoldi过程

1)选初始向量ν1=Ab/‖Ab‖;

2)for j=1,2,…,m

ωj=Aνj,

for i=1,2,…,j

hij=(ωj,νi),

ωj=ωj-hijνi,

end for

hj+1,j=‖ωj‖,

if hj+1,j=0

m=j，exit；

else

νj+1=wj/hj+1,j;

end if

end for

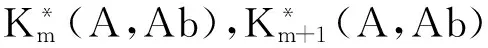
(14)

其中

Vm=[ν1,ν2,…,νm], Vm+1=[Vm,νm+1]

(15)

xj=Vjyj, yj∈Rj

那么

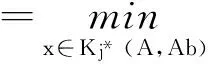
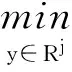
(16)

那么通过RRArnoldi过程将原问题转化为极小化问题

(17)

假设yj是式(17)的极小范数最小二乘解，那么原问题的解为xj=Vjyj,y∈Rj.

4 数值试验

文中提出的所有改进算法都进行了数值试验，并与已有的算法进行了数值比较，以显示其优越性.数值试验从matlab(2010b)工具箱“regularization tool”[7]中得到系数矩阵A，右端向量b和精确解x.算例中的α的选取与文献[8]中的取法类似.

例 求解方程Ax=b，其中系数矩阵A分别取baart、foxgood、gravity、i_laplace(2)、phillips、shaw等6类矩阵，矩阵阶数N取1 000、5 000，投影到的子空间维数m=10,20，取参数α=0.2，分别取右端扰动项ν=1%,5%,10%，其中ν=‖e‖/‖b‖.比较RRArnoldi Fractional Tikhonov正则化方法(简记为RRAFT)与RRArnoldi Tikhonov(简记为RRAT) 正则化方法的计算解与精确解相对误差范数结果如表1、2所示.

表1 N=1 000，m=10，α=0.2 RRAFT和RRAT解的相对误差比较

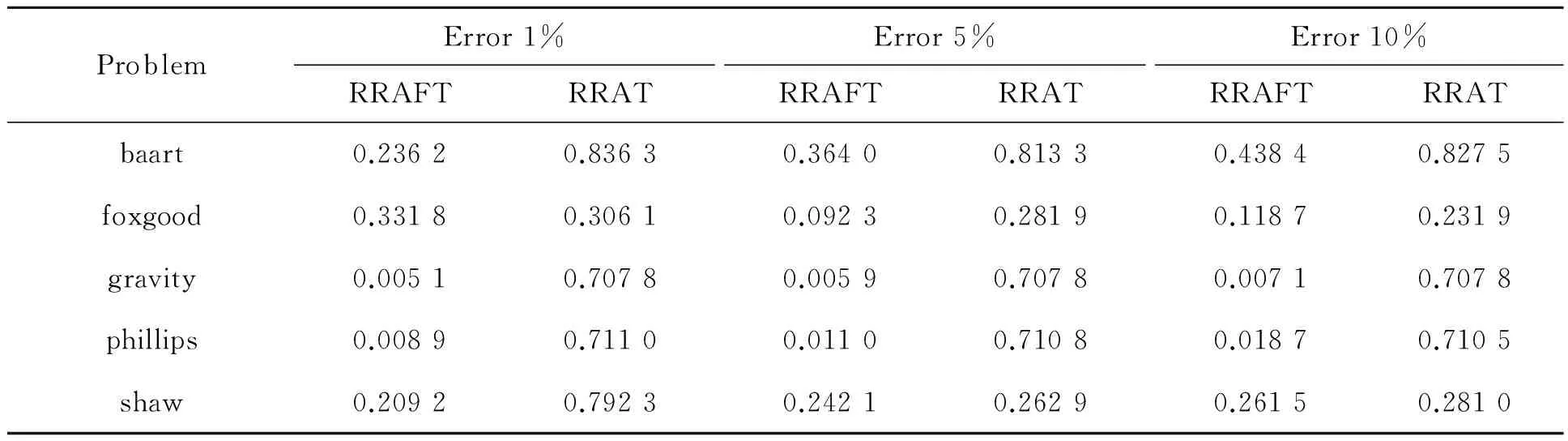
表2 N=5 000，m=20，α=0.2 RRAFT和RRAT解的相对误差比较

根据表1、2的结果可知，RRAFT的计算结果精度比RRAT的计算结果高，参数α的选取会直接影响到求解精度，数值结果显示，通过参数α的调节，计算结果精度提升较明显.

6 结语

不适定问题广泛出现在不同领域.它的求解难度在于系数矩阵的维数过大和右端项的噪音干扰.Arnoldi Fractional Tikhonov正则化方法和RRArnoldi Fractional Tikhonov正则化方法在一定程度上减轻了求解的难度.数值试验表明，新方法在求解的精度上具有一定的优势.

[1] 黄光远，刘小军.数学物理反问题[M].济南：山东科学技术出版社，1993.

[2] KIRSCH A.An introduction to the mathematical theory of inverse problems[M].NewYork:Springer- Verlag，1996.

[3] 王彦飞.反演问题的计算方法及其应用[M].北京：高等教育出版社，2007.

[4] TIKHONOV A N.Solution of incorrectly formulated problems and the regularization method[J].Soviet.Math.Dokl.，1963，4:1035-1038.

[5] HOCHSTENBACH M E，REICHEL L.Fractional tikhonov regularization for linear discrete ill-posed problems[J].BIT，2011,51:197-215.

[6] LEWIS B,REICHEL L.Arnoldi-Tikhonov regularization methods[J].J.Comput.Appl.Math.，2009，226：92-102.

[7] 肖庭延，于渗根，王彦飞.反问题数值解法[M].北京：科学出版社，2003.

[8] MORIKUNI K，REICHEL L,HAYAMI K.FGMRES for linear discrete ill-posed problems[J].Appl.Numer.Math.，2014,75：175-187.

[责任编辑 王新奇]

An Arnoldi-Fractional Tikhonov Regularization Algorithm forSolving Large Scale Linear Discrete Ill Posed Problems

ZHANG Hui

(Department of Basic, Jincheng College, Nanjing University of Aeronautics and Astronautics, Nanjing 211156, China)

The ill posed problems are widely presented in many fields such as geophysics, automatic control and so on. The regularization method is an effective method to solve the approximate solution of this kind of problem. In this paper, the Fractional Tikhonov regularization algorithm is applied to the projection algorithm. Firstly, an Arnoldi-Fractional Tikhonov regularization algorithm is proposed for solving large-scale linear discrete ill posed problems. Secondly, an Arnoldi-Fractional Tikhonov regularization algorithm of restricted range is put forward. And numerical experiments and comparisons are carried out for the classical examples. The numerical experiment results show that the new algorithm is effective and has more advantages.

ill posed problem; regularization method; Fractional regularization method; Fractional Tikhonov regularization algorithm

1008-5564(2016)04-0017-05

2016-02-09

张 慧(1990—)，女，安徽马鞍山人，南京航空航天大学金城学院基础部助教，硕士，主要从事数值代数研究.

O411

A