Reliable single epoch ambiguity resolution for precise attitude determination using BeiDou triple-frequency observations

WU Ming-kui, HE Jun, WANG Hong-Chen(. School of Geodesy and Geomatics, Wuhan University, Wuhan 40079, China; . China ship design and development center,Wuhan 40064, China; . Research and development office, Wuhan University, Wuhan 4007, China)

Reliable single epoch ambiguity resolution for precise attitude determination using BeiDou triple-frequency observations

WU Ming-kui1, HE Jun2, WANG Hong-Chen3
(1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China; 2. China ship design and development center,Wuhan 430064, China; 3. Research and development office, Wuhan University, Wuhan 430072, China)

In view that the carrier-phase integer ambiguity resolution (AR) is critical to the high-precision attitude determination of GNSS, a fast and reliable single epoch AR approach is proposed for BeiDou triple-frequency attitude determination with baseline length constraint. Firstly, two extra wide-lane (EWL)ambiguities are reliably resolved using a geometry-free approach. Then a wide-lane (WL) combination,which is less affected by observation noise and ionospheric delay, is derived from the former two EWL ambiguities. Followed by the third narrow-lane (NL) ambiguity, which is linearly independent from the former two EWL ambiguities, is estimated using the geometry-free approach and is fixed using a constrained least-squares ambiguity decorrelation adjustment (C-LAMBDA) method. Finally, the three original carrier ambiguities are uniquely recovered and used for instantaneous attitude determination. The performance of the proposed approach is evaluated using raw BeiDou triple-frequency data collected by receivers from different manufacturers and types in both static and kinematic situations. The results demonstrate that the proposed approach can deliver relatively high AR success rate with high computational efficiency. Moreover, the proposed approach is insensitive to the occurrences of troublesome carrier-phase cycle slips as the ambiguities are resolved epoch by epoch. The proposed approach is fairly suitable for the data processing in multi-frequency GNSS based attitude determination applications with high data sampling rate under complicated kinematic environments.

BeiDou; triple-frequency; single-epoch; attitude determination; C-LAMBDA

The Chinese BeiDou navigation satellite system(BDS) has attained initial regional operational status over the Asian-Pacific region since December 27, 2012, with a constellation of five satellites in Geostationary Orbit(GEO), five satellites in Inclined Geosynchronous Orbit(IGSO), and four satellites in Medium Earth Orbit(MEO). Each of the satellites transmits signals on three frequencies, namely 1561.098 MHz on B1frequency,1207.14 MHz on B2frequency, and 1268.52 MHz on B3frequency respectively. As an alternative to GPS, BDS has attracted widespread interests in fields of high precision applications such as GNSS based attitude determination[1-3]. Because of its advantages of high precision,no error accumulation, low power consumption and low cost, GNSS based attitude determination has attracted much attention in recent researches with a variety of challenging applications on land, at sea, in air and space[4-8].

The key to fast and high precision GNSS based attitude determination is the resolution of the unknown cycle ambiguities. Once this has been done successfully,the carrier phase observations will act as very precise pseudorange data, thus making very precise attitude determination possible. Many algorithms have been proposed and used for integer ambiguity resolution(AR) in GNSS based attitude determination[9-17], among which the constrained Least-squares AMBiguity Decorrelation Adjustment (C-LAMBDA) method is generally accepted as the optimal one. The C-LAMBDA method can fully integrate the nonlinear baseline constraint into the ambiguity objective function and does proper justice to this a priori information, thus leading to a higher success rate than other methods[15-16].

The C-LAMBDA method is generally used with original observation equations on each frequency[2-6,15-16].In that case, the advantage of multi-frequency ambiguity resolution is not fully employed. Compared to singlefrequency and dual-frequency observations, various linear combinations with special properties (long wavelength, minimal ionospheric and noise scale factors)can be formed using triple-frequency observations. This means that there is no need to resolve all the ambiguities on three frequencies on a whole as it is time-consuming.Instead, we can fix them in a cascading approach[18-23].Unfortunately, most of the studies focus on the long baseline case. Little attention has been paid to its special application of attitude determination.

In this contribution, a fast and reliable single epoch AR approach is proposed for BDS triple-frequency attitude determination with baseline length constraint.Two extra wide-lane (EWL) (λ>2.93 m) ambiguities are reliably fixed using the geometry-free approach. Then a wide-lane (WL) (0.75 m<λ<2.93 m) combination, which is less affected by observation noise and ionospheric delay, is derived from the former two ambiguity resolved EWL combinations. Followed by a narrow-lane (NL)(λ<0.75 m) ambiguity combination, which is linearly independent from the former two EWL ambiguities, is estimated using the ambiguity resolved WL observations and fixed using C-LAMBDA method. Finally the ambiguities of the three original carrier phase observations are uniquely recovered and used for precise attitude determination. Since the WL combination is less affected by ionospheric delay and observation noise, the estimated float NL ambiguities can be more accurate than those estimated from original pseudorange observations. In addition, the number of the float NL ambiguities for searching in the proposed approach is much less than those from the traditional methods. As a consequence,the proposed triple-frequency AR approach can be more computational efficient. Moreover, the resolution of the three linearly independent EWL/NL combinations is performed epoch by epoch, thus making it free from the troublesome cycle slips which occur frequently in the kinematic situations.

1 BDS triple-frequency AR model for attitude determination

1.1 Triple-frequency observation equations

Considering BDS Bi(i=1,2,3) frequency pseudorange Riand carrier phase Li(expressed in unit of meters),the BDS triple-frequency combination of doubledifferenced (DD) pseudorange and carrier phase observation equations can be expressed as

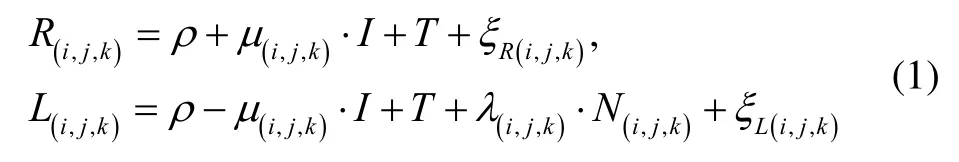
Where R(i,j,k)triple-frequency combination of DD pseudorange, L(i,j,k)triple-frequency combination of DD carrier phase observation in unit of meters, ρ geometric distance between satellite and receiver, μ(i,j,k)first-order ionospheric scale factor of combined observations, I firstorder ionospheric delay on B1frequency, T tropospheric delay, λ(i,j,k)wavelength of combined carrier phase observations, N(i,j,k)integer ambiguity of combined carrier phase observations, i, j, k integer combination coefficients on B1, B2, B3frequencies respectively, ξR(i,j,k)combined DD pseudorange noise, and ξL(i,j,k)combined DD carrier phase noise.

Triple-frequency linear combination of pseudorange and carrier phase observations in Eq.(1) can be generally formulated as[19]

Where firepresents BDS Bifrequency. Replacing Liwith λi·φiin the second equation of Eq.(2) yields

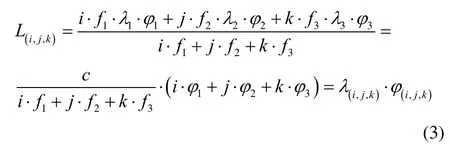
Where φ(i,j,k)is the triple-frequency carrier phase combination expressed in unit of cycles, c is the speed of light in vacuum and

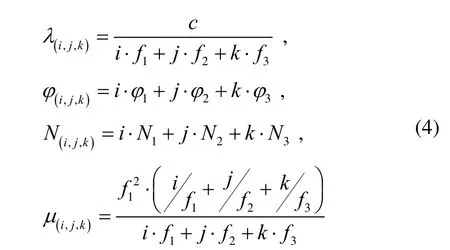
Assuming the noise terms (in unit of meters) for the original pseudorange or carrier phase observations are independent and identical in variance, i.e.with “*=R” for pseudorange and “*=L” for carrier phase, the variances of the combined pseudorange and carrier phase measurements can be expressed as

1.2 Geometry-free AR model

By differencing the first and second observation equations in Eq.(1), one can obtain the geometry-free AR model

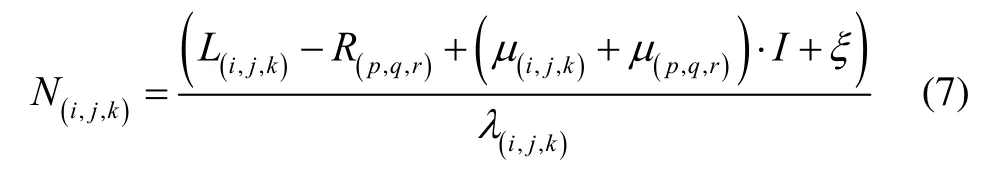
Where the (i, j, k) and (p, q, r) are the coefficients of the carrier phase and pseudorange combinations respectively,and ξ is the combined observation noise of the phase and pseudorange combinations. Note that the pseudorange combination R(p,q,r)can be replaced by another ambiguity resolved phase combinationas

N(i,,j,k)can be simply resolved by integer rounding.Whether the combined ambiguity N(i,,j,k)can be successfully rounded to an integer by Eq.(7) and Eq.(8)depends mainly on the effect of uncertainty terms. This requirement yields the criterion for selecting the optimal combination coefficients

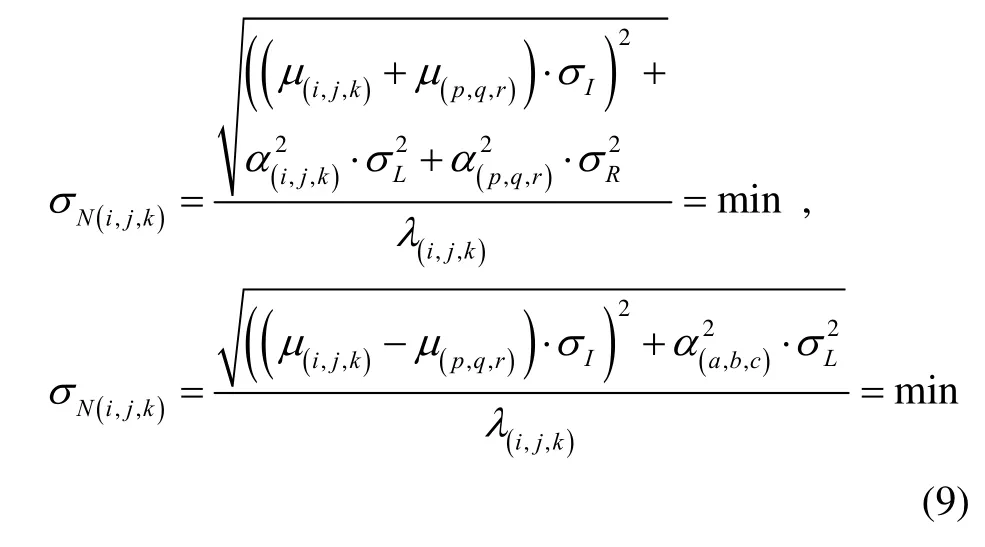
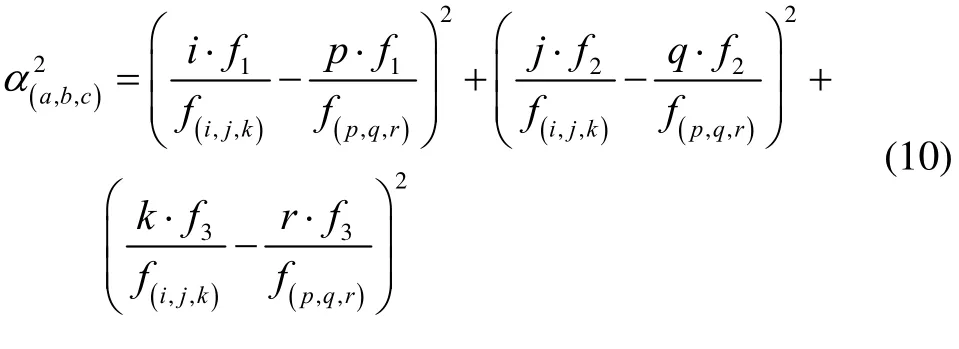
1.3 Geometry-based AR model with baseline length constraint

Assuming n+1 satellites are simultaneously observed in a certain epoch, the linearized form of Eq.(1) with known baseline length l can be expressed as[15]

The variance-covariance (VC) matrix Qyyis expressed as

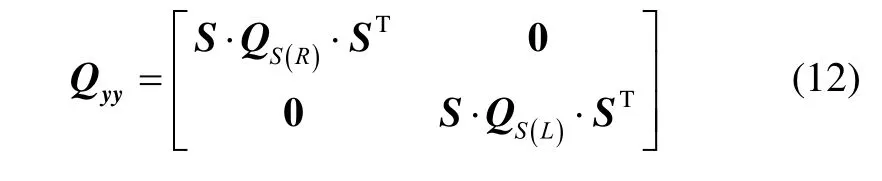
From Eq.(11), z and b can be solved for by applying the constrained least-squares adjustment with the objective function

When applying the geometry-based AR model, the combinations with minimal ionospheric and noise scale factors with respect to their wavelengths are preferred.Taken this into account, the optimal combination for the geometry-based AR can be identified by[19]

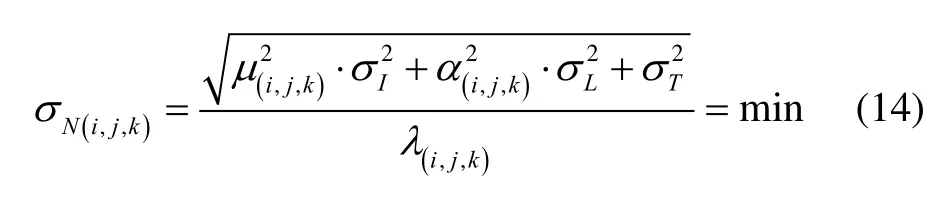
WhereTσ denotes the standard deviation for the tropospheric delay.

Provided that the baseline vector of the two GNSS antennas is parallel to the moving direction of the corresponding platform. The heading H and the elevation E can be computed as

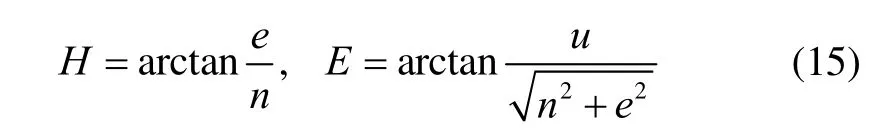
Where e, n, u are the local coordinates with e the east direction, n the north direction and u the up direction,respectively.

2 Instantaneous BDS triple-frequency AR approach

Among the various triple-frequency linear combinations, the EWL combinations are outstanding for their extraordinary long wavelengths. AR for elaborately selected EWL combinations can even be accomplished epoch by epoch with the simple geometry-free approach.Consistent with most literatures[19-23], the BDS B2and B3Melbourne-Wübbena (MW) combination, which is free of both ionospheric and tropospheric delay, is used for geometry-free AR in the first step of our procedure. Fig.1 showsin Eq.(9) as a function of DD codestandard deviations (STD). It can be seen that the noise level for N(0,-1,1)would generally not exceed 0.2 cycles. This indicates that the probability of obtaining correct integers of N(0,-1,1)by the integer rounding with a single epoch observations can be above 98%[19].

After the resolution of N(0,-1,1), the ambiguity resolved EWL observationand phase is used in Eq.(7)instead of the less precise pseudorange combination R(p,q,r). According to [18], the best combinations in terms of long wavelength and low ionospheric delay are all belong to the so-called S0group, which is characterized by

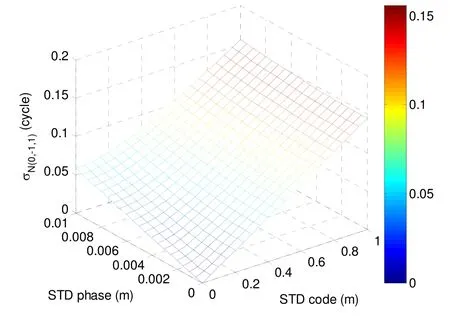
Fig.1 vs. DD code and phase noise

By substituting Eq.(16) into Eq.(9) and replacingL(p,q,r)with ambiguity resolved, one obtains:

In order to identify the best integer coefficientsiandjthat satisfies Eq.(17), the standard deviations of the DD ionospheric delay and phase observation are fixed to a general value which best fits the ultra-short baseline case:Iσ=5 cm,Lσ=0.5 cm. By setting the range foriandjas –50 to 50, the minimal value foris obtained and shown in Table 1.

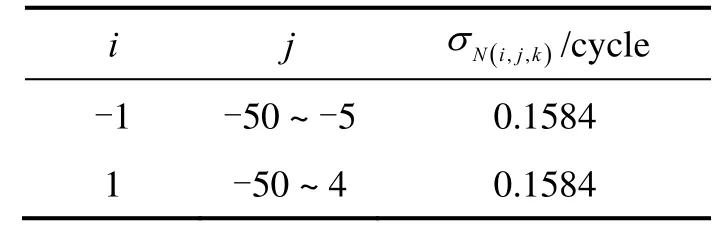
Tab.1 The second optimal combination

It can be seen from Table 1 that the second optimal combination is not unique. These optimal combinations can be classified into two groups: the first group with coefficientiequal to –1 and the second group withiequal to 1. The noise level for the ambiguity of the second optimal combination in geometry-free mode is about 0.1584 cycles in general. Fig.2 illustrates the wavelengths of these optimal combinations. It’s shown that most of the combinations have a wavelength close to zero. Only a few combinations have a wavelength longer than 1m and the longest one has a wavelength of about 21 m. We employL(1,4,-5)as the second optimal combination in this paper. Fig.3 shows the noise level forN(1,4,-5)with ambiguity resolved measurement combination. The standard deviations of the phase observation and ionosphere are assumed to vary from 0 to 0.01 m and from 0 to 0.1 m, respectively. From Fig.3, it can be concluded thatis more sensitive to the change of the phase standard deviation. When the standard deviation of the phase observation increases to 0.01 m,reaches its maximum value of about 0.3 cycles.As a consequence, the ambiguity resolution of the second optimal combination is still reliable using the geometryfree approach.

Fig.2 λ of the second candidate optimal combination

Fig.3 vs. ionosphere and phase noise

After the resolution ofN(0,-1,1)andN(1,4,-5), any ambiguity combinations with the sum of coefficients being equal to 0, can be derived. In order to recover the original ambiguities onB1,B2andB3frequencies, a third ambiguity combination, which is linearly independent fromN(0,-1,1)andN(1,4,-5), should be resolved. In this step,the third admissible combination has to be taken from the S1group, which is characterized by the sum of coefficients being equal to 1. Fig.4 illustrates the noise level for ambiguity resolution of the third combination under geometry-free mode. The coefficientsiandjare selected between -10 and 10. According to the figure, the minimal noise level of the third combination in S1group exceeds 0.5 cycles, which is too noisy for reliable integer rounding. As a consequence, the geometry-based mode should be used instead. Eq.(14) is used as criterion to identify the optimal combination in the third step. Table 2 lists the first 10 optimal combinations for the third step,in which the double differenced troposphere, ionosphere and phase noise is set to 2 cm, 5 cm and 0.5 cm respecttively. It can be seen from the table that these optimal combinations all belong to the NL group with a wavelength smaller than 0.75 m. The noise level of all these combinations is almost the same. So it makes no sense to choose which one from the table. In this paper, linear combination ofL(3,-2,0)is used as the third combination.

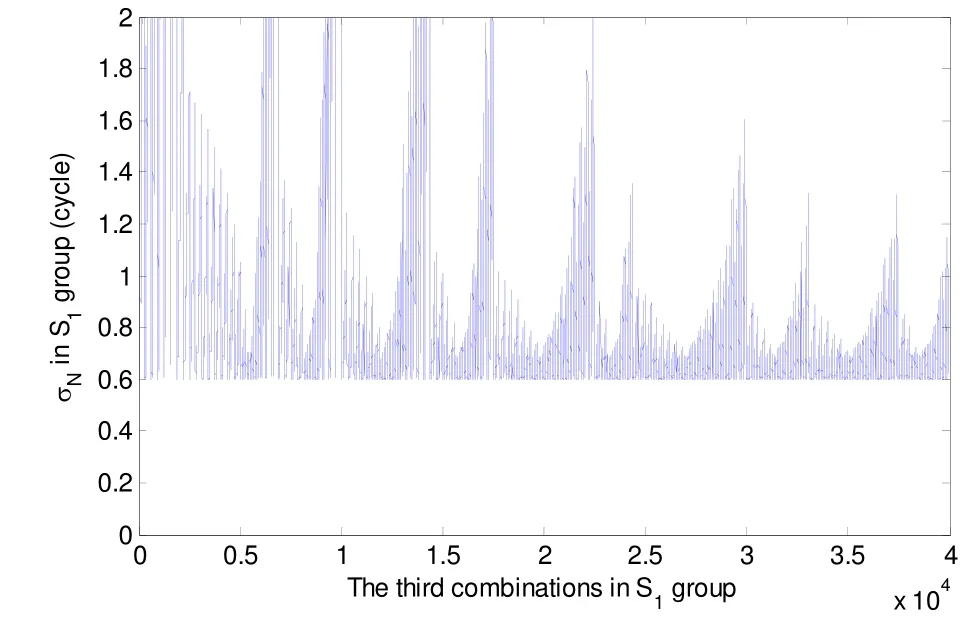
Fig.4 Nσof the third combination

Tab.2 First 10 optimal combinations in the third step

Tab.3 First 10 optimal combinations with minimum TNL in unit of meters from S0 group

In order to get a more accurate float solution in the third step, the liner combination derived from the two ambiguity-fixed EWL combinations should be as precise as possible. Table 3 lists the best 10 combinations in S0group with a minimal TNL value in unit of meters. These combinations are also selected by setting coefficients from –10 to 10. As can be seen from the table, the TNLs for these combinations show insignificant difference between each other. This indicates that precise pseudorange observations with about decimeter accuracy (about 0.072 m) can be achieved in single epoch with the selected combinations. As a result, the combinations listed in Table 3 can be used to assist the ambiguity resolution of the linearly independent combination in the third step. In this paper, linear combination ofL(2,-1,-1)is used and can be calculated by

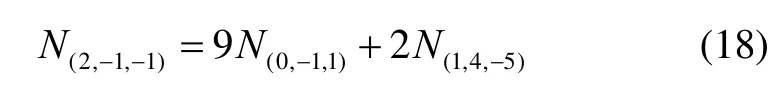
Considering the discussion above, the proposed instantaneous triple-frequency attitude determination procedure is summarized as follows and shown in Fig.5:

1) Geometry-free AR for the resolution ofN(0,-1,1)withB2/B3frequency MW combination;

2) Geometry-free AR for the resolution ofN(1,4,-5)with the ambiguity resolved

3) Compute the ambiguity ofN(2,-1,-1)by Eq. (18). Then perform geometry-based AR forN(3,-2,0)with the ambiguity resolved observation, during which the C-LAMBDA method is applied;

4) Recover the original ambiguities onB1,B2,B3frequencies and perform instantaneous attitude determination.

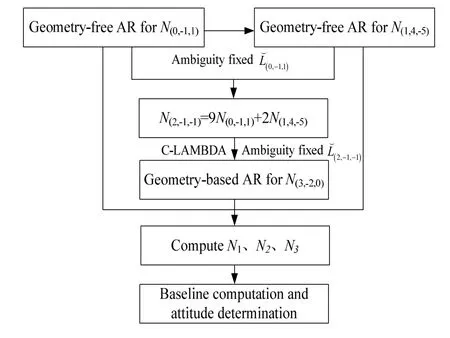
Fig.5 Flowchart of the proposed instantaneous triple-frequency attitude determination approach

3 Performance of instantaneous triple-frequency AR of BDS based attitude determination

In this section, the performance of the proposed approach is evaluated with four sets of raw BDS triplefrequency data collected in Wuhan, China. The receivers involved in the experiments include Trimble NetR9,ComNav K505, ComNav K508, and Unicore UB370. The detailed description of the data sets is listed in Table 4.The trajectory and velocity of the cars for each kinematic experiment are illustrated in Fig.6.

Tab.4 BDS triple-frequency data sets

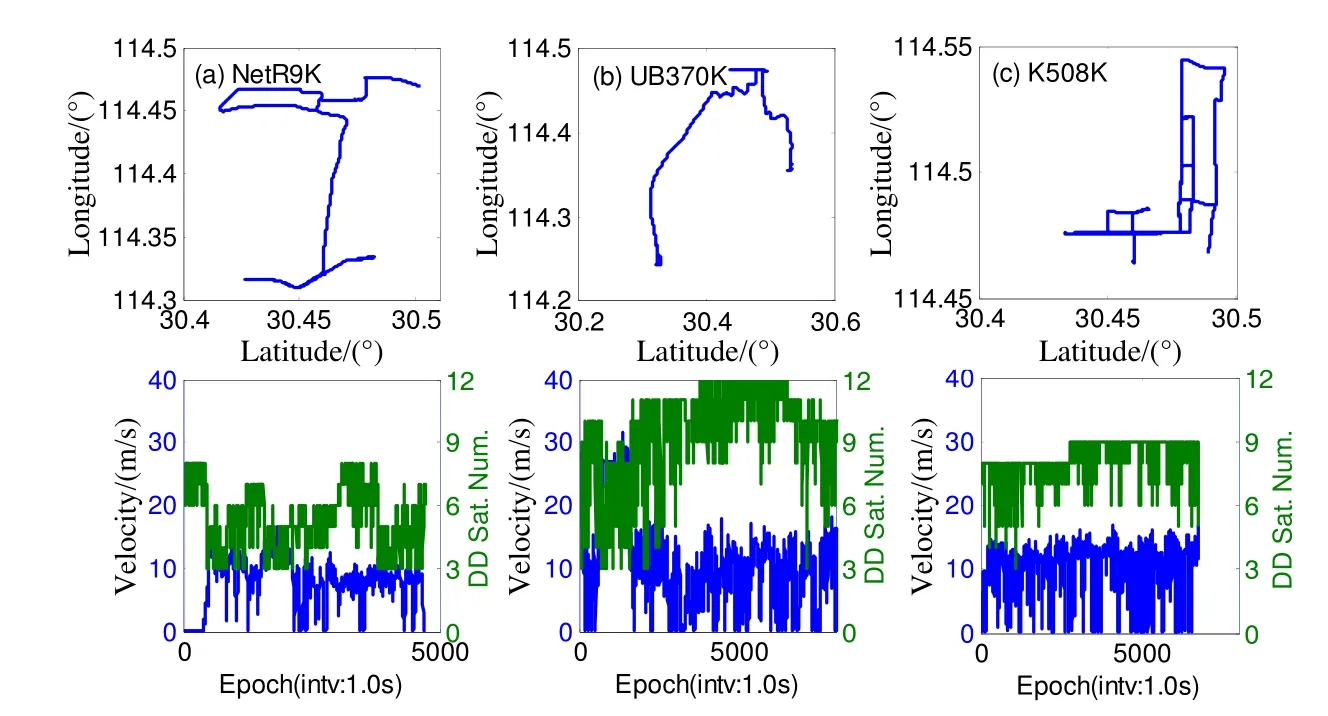
Fig.6 Trajectory (top) and velocity (bottom) of the cars

3.1 Geometry-free AR for N(0,-1,1) and N(1,4,-5)

As mentioned above,N(0,-1,1)andN(1,4,-5)can be reliably resolved by the geometry-free approach. The offsets between the float ambiguities calculated by the geometry-free AR approach and their nearest integer values are shown in Fig.7. It can be seen that the offsets between the float and integer ambiguities forN(0,-1,1)would not exceed 0.2 cycles for all the four data sets.Most of the offsets are even below 0.1 cycles for experiments K508K and K505S (Fig.7(c) and Fig.7(d)).These results are consistent with the theoretical analysis demonstrated by Fig.1. With such small offsets between the float ambiguities and their nearest integers,N(0,-1,1)can be resolved reliably by integer rounding. Except for experiment NetR9K, the offsets between the float and integer ambiguities forN(1,4,-5)is a little larger thanN(0,-1,1), which means that the AR ofN(1,4,-5)is slightly difficult thanN(0,-1,1). However, these offsets are below 0.3 cycles for most epochs, which means thatN(1,4,-5)can still be reliably resolved.

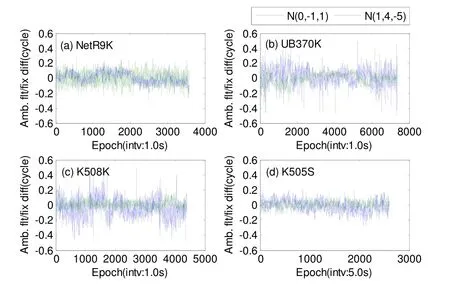
Fig.7 Offsets of float ambiguities and their corresponding integer values for N(0,-1,1) and N(1,4,-5)

3.2 Geometry-based AR for N(3,-2,0)

After the resolution ofN(0,-1,1)andN(1,4,-5), the ambiguity forL(2,-1,-1)can be easily derived from Eq.(18) and used for the resolution ofN(3,-2,0). Empirical success rate and computing time are used to evaluate the performance of geometry-based AR forN(3,-2,0). The empirical success rate is defined as

These numbers are determined by comparing the estimated ambiguities to the true ambiguities, which are solved by using a combined system with multiple frequencies and a Kalman filter over the whole time-span.The computing time refers to the time consumed to get the integer ambiguities from the float ones in the C-LAMBDA method.

Fig.8 demonstrates the empirical AR success rate for the above four data sets. “single”, “dual” and “trip”represent the traditional geometry-based AR using original single-frequency, dual-frequency, and triplefrequency observations with C-LAMBDA method respecttively. “trip-m” represents the proposed approach.

It is shown that the empirical AR success rate using single-frequency observations is obviously lower than the dual-frequency or triple-frequency case. The proposed approach can provide almost identical AR success rate in comparison to the traditional triple-frequency geometrybased AR using C-LAMBDA method in the K508K and K505S experiments. However, it’s a little lower in the NetR9K and UB370K experiments. This is reasonable considering that the signal onB3frequency sometimes lose track for one or two satellites in the two experiments.These satellites cannot be used in the proposed approach while they can still be used in the traditional geometrybased AR using original triple-frequency observations.

Fig.8 Empirical success rate for instantaneous AR

Fig.9 Time consumed by the C-LAMBDA method

Fig.9 demonstrates the time consumed by the C-LAMBDA method for the four approaches. It’s shown that the time consumed by the proposed triple-frequency AR approach is slightly less than that consumed by the traditional single-frequency approach in K508K and K505S experiments. However, the improvement is significant in NetR9K and UB379K experiments. This is because that the ambiguity fixed WL observations used for calculating the float ambiguities ofN(3,-2,0)in the proposed approach is more precise than the originalB1pseudorange, which is used to determine theB1float ambiguities in the traditional single-frequency approach.On the other hand, the time consumed by the proposed triple-frequency AR approach is much less than that consumed by the traditional dual-frequency or triplefrequency approach. This is reasonable considering that the number of float ambiguities for traditional dualfrequency and triple-frequency approach are twice and three times the number of the proposed triple-frequency approach.

From Fig.8 and Fig.9, it can be concluded that the proposed approach can deliver relatively high AR success rate with high computational efficiency.

4 Conclusions

In this contribution, a fast and reliable single epoch AR approach is proposed for BDS triple-frequency attitude determination with baseline length constraint.The proposed approach consists of three major steps,namely the geometry-free AR for two EWL ambiguities and the geometry-based AR for a third independent NL ambiguity with C-LAMBDA method. In order to ensure the reliability of ambiguity resolution, a detailed analysis concerning the error characteristics of the geometry-free and geometry-based AR for the selected EWL, WL, and NL ambiguity combinations is carried out. The performance of the proposed approach is demonstrated using raw BDS triple-frequency data collected by different receivers in both static and kinematic situations.It’s demonstrated that the proposed approach can deliver relatively high AR success rate with less consuming time, in comparison to the traditional geometrybased AR using original observations with C-LAMBDA method.

[1]Lu L, Li Y, Rizos C. Virtual baseline method for Beidou attitude determination: an improved long-short baseline ambiguity resolution method[J]. Advances in Space Research, 2013, 51(6): 1029-1034.

[2]Nadarajah N, Teunissen P J G, Raziq N. Instantaneous BeiDou-GPS attitude determination: a performance analysis[J]. Advances in Space Research, 2014, 54(5): 851-862.

[3]Nadarajah N, Teunissen P J G. Instantaneous GPS/BeiDou/Galileo attitude determination: a single-frequency robustness analysis under constrained environments[J].Navigation: Journal of the Institute of Navigation, 2014,61(1): 65-75.

[4]Giorgi G, Teunissen P J G, Verhagen S, et al. Testing a new multivariate GNSS carrier phase attitude determination method for remote sensing platforms[J]. Advances in Space Research, 2010, 46(2): 118-129.

[5]Giorgi G, Teunissen P J G, Gourlay T P. Instantaneous global navigation satellite system (GNSS)-based attitude determination for maritime applications[J]. IEEE Journal of Oceanic Engineering, 2012, 37(3): 348-362.

[6]Teunissen P J G, Giorgi G, Buist P J. Testing of a new single-frequency GNSS carrier phase attitude determination method: land, ship and aircraft experiments[J]. GPS Solutions, 2011, 15(1): 15-28.

[7]Unwin M, Purivigraipong P, da Silva Curiel A, et al.Stand-alone spacecraft attitude determination using real flight GPS data from UOSAT-12[J]. Acta Astronautica,2002, 51(1): 261-268.

[8]Zhang X, Wu M, Liu W. Receiver time misalignment correction for GPS-based attitude determination[J]. Journal of Navigation, 2015: 1-19.

[9]Chen W, Qin H. New method for single epoch, single frequency land vehicle attitude determination using lowend GPS receiver[J]. GPS Solutions, 2012, 16(3): 329-338.

[10]Dai L, Ling K V, Nagarajan N. Real-time attitude determination for microsatellite by LAMBDA method combined with Kalman filtering[C]//Proceedings 22nd AIAA International Communications Satellite Systems Conference and Exhibit. 2004.

[11]Giorgi G, Teunissen P J G. Low-complexity instantaneous ambiguity resolution with the affine-constrained GNSS attitude model[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1745-1759.

[12]Monikes R, Wendel J, Trommer G F. A modified LAMBDA method for ambiguity resolution in the presence of position domain constraints[C]//Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005). 2005: 81-87.

[13]Park C, Kim I, Lee J G, et al. Efficient ambiguity resolution using constraint equation[C]//Position Location and Navigation Symposium. IEEE, 1996: 277-284.

[14]Park C, Teunissen P J G. A new carrier phase ambiguity estimation for GNSS attitude determination systems[C]//Proceedings of International GPS/GNSS Symposium.Tokyo, 2003.

[15]Teunissen P. The LAMBDA method for the GNSS compass[J]. Artificial Satellites, 2006, 41(3): 89-103.

[16]Teunissen P J G. Integer least-squares theory for the GNSS compass[J]. Journal of Geodesy, 2010, 84(7): 433-447.

[17]Wang B, Miao L, Wang S, et al. A constrained LAMBDA method for GPS attitude determination[J]. GPS Solutions,2009, 13(2): 97-107.

[18]Cocard M, Bourgon S, Kamali O, et al. A systematic investigation of optimal carrier-phase combinations for modernized triple-frequency GPS[J]. Journal of Geodesy,2008, 82(9): 555-564.

[19]Feng Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy,2008, 82(12): 847-862.

[20]Li B, Feng Y, Shen Y. Three carrier ambiguity resolution:distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J]. GPS Solutions, 2010, 14(2): 177-184.

[21]Tang W, Deng C, Shi C, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. GPS Solutions, 2014, 18(3): 335-344.

[22]Zhang X H, He X Y. BDS triple-frequency carrier-phase linear combination models and their characteristics[J].Science China Earth Sciences, 2015, 58(6): 896-905.

[23]Zhang X, He X. Performance analysis of triple-frequency ambiguity resolution with BeiDou observations[J]. GPS Solutions, 2016, 20(2): 269-281.

北斗三频精密姿态测量中整周模糊度的单历元可靠固定

吴明魁1，何 俊2，汪宏晨3

（1. 武汉大学测绘学院, 武汉 430079；2. 中国舰船研究设计中心，武汉 430064；3. 武汉大学科学技术发展研究院，武汉 430072）

载波相位模糊度固定是GNSS高精度姿态测量中的关键问题。针对附有基线长约束的姿态测量场景提出了一种可靠的 BeiDou三频模糊度单历元快速固定算法。首先使用无几何模型可靠地固定两个超宽巷模糊度；其次使用这两个超宽巷模糊度计算一个宽巷模糊度；然后在固定模糊度的宽巷观测值的辅助下，使用几何相关模型对第三个窄巷模糊度（该模糊度需与两个超宽巷模糊度线性独立）的浮点解进行估计，并使用C-LAMBDA方法对其进行固定；最后对三个频点上的原始模糊度进行恢复并利用其进行单历元姿态测量。多组 BeiDou三频实测数据的处理结果表明，提出的单历元模糊度固定方法具有固定成功率高和计算速度快的特点，能够有效地避免周跳的影响，非常适合高采样、动态复杂环境下的多频GNSS姿态测量数据处理应用。

北斗；三频；单历元；姿态测量；C-LAMBDA

P228.41

A

1005-6734(2016)05-0624-09

10.13695/j.cnki.12-1222/o3.2016.05.012

2016-06-28；

2016-09-28

国家重点研发计划（2016YFB0501803）；国家自然科学基金（41204030）；湖北省自然科学杰出青年基金（2015CFA039）

吴明魁（1988—），男，博士研究生，从事GNSS精密导航定位技术及应用研究。E-mail: wmk@whu.edu.cn

联 系 人：汪宏晨（1974—），男，副教授。E-mail: wanghc@whu.edu.cn