鲁棒图局部坐标编码*
印爽
(辽宁师范大学数学学院,辽宁大连116029)
鲁棒图局部坐标编码*
印爽
(辽宁师范大学数学学院,辽宁大连116029)
文章将局部坐标编码(NGLF)和图非负矩阵分解(GNMF)合并形成新框架,并用L2,1范数代替原始L2范数构成新的目标函数,提出新的鲁棒图局部坐标分解(RGLCF)算法.新算法在使数据行稀疏的同时也确保数据在几何结构上具有鲁棒性,给出了算法的更新规则并对算法的收敛性进行了证明.
非负矩阵分解;局部坐标;图正则;聚类
近几年特征提取已经受到广泛关注,特征提取的变体模型如主成分分析(PCA)[1],奇异值分解(SVD),非负矩阵分解(NMF)[2-3]和CF[4]被研究用于找到高维数据的一个低维表示.然而,在实际应用程序中总会涉及到数据,当测量重组误差时,成平方的损失对异常点和噪声是敏感的,最近一些提高NMF鲁棒性的模型已经被提出,Zhang et al提出了鲁棒非负矩阵分解,将数据矩阵分解成一个稀疏误差矩阵和两个非负矩阵的和.Kong et al提出了基于L21范数的鲁棒NMF,能够解决噪声和异常点.Zhang et al提出的鲁棒非负图嵌入(GNGE)可以同时解决噪声数据及其分布.
本文中,提出了一个新的矩阵分解方法,鲁棒图局部坐标编码(RGLCF).图正则方法构造样本间的相似关系图刻画数据的流形结构.然而GNMF模型的目标函数采用的是L2范数的平方误差,在实际应用中数据容易受到噪声数据的干扰,无法准确反映应有的特征,严重降低了聚类效果,NLCF模型同样对噪声和异常点非常敏感,分类效果都不十分理想.本文采用比L2范数更具有鲁棒性的L21范数,解决了数据中的噪声干扰,异常点及不良图对原始数据的影响,聚类效果得到显著增强.
1 相关工作
本文中,对于向量,x∈R,x的Lp范数定义为;矩阵X=(xij)中,用x(i),x(j)分别代表矩阵X的第i行和第j列,xij表示矩阵X的第i行第j列数.Tr[X]代表矩阵X的迹.矩阵X∈RM×N的F范数记为矩阵的2,1范数可看成是L1范数的旋转不变量,定义为以看出2,1范数对旋转矩阵R的行保持旋转不变性,几乎处处有‖XR‖2,1.X中与非零行有关的特征被选择下来,特征选择通过这种方法来实现.
给定一个非负矩阵X=[X(1),X(2),…,XN]∈RM+×K,X的每列可看为一个数据点.NMF是要找到两个非负矩阵,使得目标函数最小,V≥0,这里‖·‖F是F范数.目标函数对U或V分别是凸函数,但对U和V不再是凸函数.因此,很难找到解决上述问题的一个全局最优解.Lee et al.提出了如下的更新规则对目标函数进行优化←
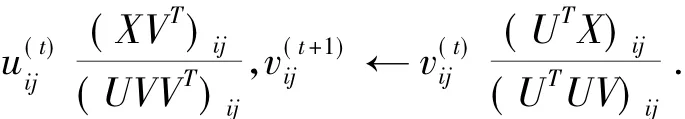
2 RGLCF框架
2.1 鲁棒局部坐标编码
局部坐标编码可定义为一个概念对(γ,C),其中C是具有d维的锚点集合,γ是从x∈Rd到[γv(x)]v∈C∈R|C|的映射.NMF模型可以看成一个坐标编码,这里基矩阵U的列向量就是锚点的集合,系数矩阵V的列向量则包含了对应于每个锚点的系数.为了获得稀疏编码,每一个数据点需要被表示成由附近少数锚点的线性组合.通过下面介绍的局部坐标约束能够做到这一点:
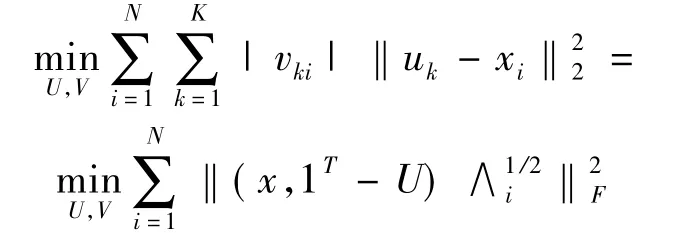
局部坐标编码采用的平方误差对噪声和异常值都很敏感,为了减少不相关和噪声数据的影响,我们提出如下局部坐标编码的聚类问题.
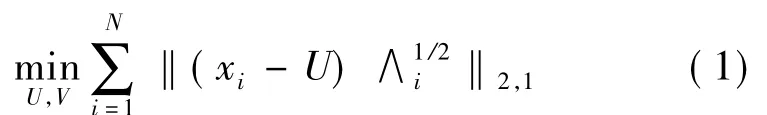
局部坐标编码不带平方项,因此较大异常值和噪声不会影响目标函数.
2.2 鲁棒图非负矩阵分解
NMF可找到一组欧氏距离最能够接近原始数据的基向量,却不能反映本征数据结构,为了使局部约束能很好地反映本征数据结构,需要考虑数据空间中的流形几何结构,而且已经证明数据的局部几何结构可用分散数据的近邻图刻画,因此提出如下目标函数
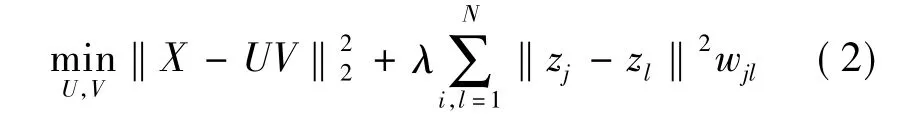
从上式可以看出两个问题,第一,样本重组误差是带平方的,较大误差的噪声样本容易影响目标函数.第二,图非负矩阵分解也受不良解构图的影响.为了使目标函数对噪声数据和不良图具有鲁棒性,提出如下公式
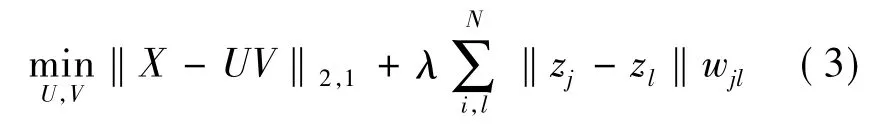
2.3 RNLCF的目标函数
将鲁棒局部坐标编码(1)和鲁棒图非负矩阵分解(3)合并形成一个新的框架.RNLCF的整体目标函数被定义为这里μ是权系数,称(4)为鲁棒图局部坐标编码.
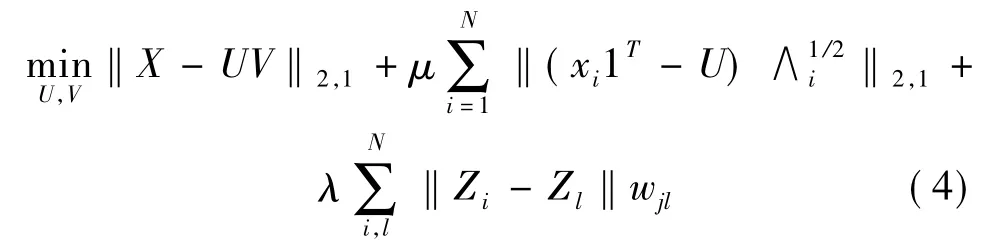
3 优化
优化问题(4)涉及的L2,1范数是非平滑的,为了解决这个问题,应用L2,1范数的变体形式.由矩阵性质有,Tr(A),其中∧i=diag(|vi|)∈RK×K.
考虑到U和V的非负限制,目标函数(4)可以改写成

其中A,B,C为对角矩阵,对应的对角线元素分别为
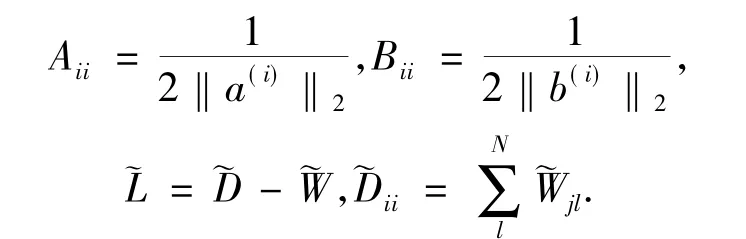
目标函数(5)对于U和V是非凸的,因此不能找到一个可算出全局最小值的算法,下面介绍一种能够找到局部最小值的更新规则,通过计算目标函数可被写成:

令φij,φij是限制uij≥0和vij≥0相应的拉格朗日乘数,Ψ=[φij],Φ=[φij].其拉格朗日函数L可写成
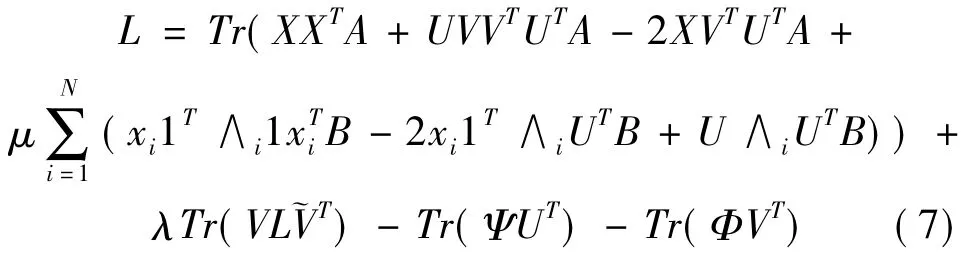
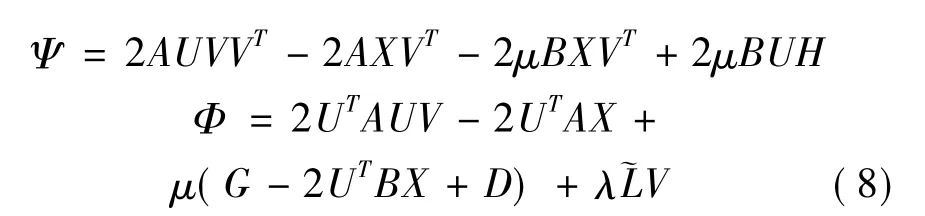
这里H是由V的行之和组成的对角矩阵.
定义g=diag(XTBX)∈RN,令G=(g,…,g)T是K×N维矩阵;定义d=diag(UTBU)∈RK,令D =(d,…,d)是K×N维矩阵.按照KKT条件φijuij=0和φijvij=0.可得到如下等式:
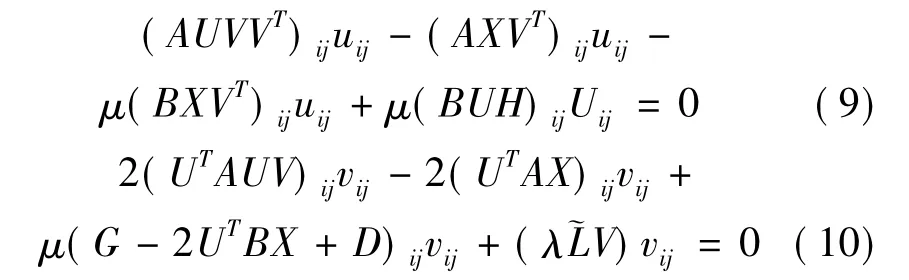
解决式子(9)和(10),有如下更新规则

定义1 Z(h,h')为F(h)的辅助函数,满足Z(h,h')≥F(h),Z(h,h)=F(h).
引理1 如果Z(h,h')是F的辅助函数,那么F在如下更新规则是单调递减函数
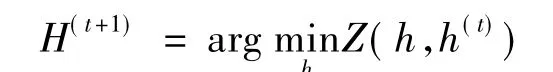
引理2 对任意非负矩阵A∈Rn×n、B∈Rk×k、S∈Rn×k、S'∈Rn×k且A和B是对称矩阵,则满足不等式
本文算法收敛性正确性如下:
对于给定的X,固定U,用O(V)表示目标函数中至于V相关的部分,则

定理1 函数Z(V,V')=-2Tr(UTAXVT)-+ μ∑Gij是 O(V)的一个辅助函数.
因为Z(V,V')满足辅助函数的定义,那么它对v来说是一个凸函数,则有全局极小值
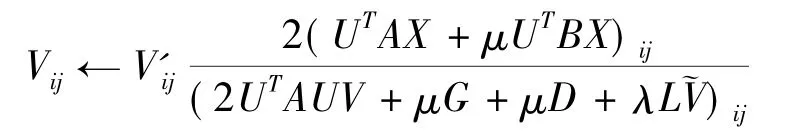
证明 Z(V,V')=O(V)是显然的,只需证Z(V,V')≥O(V).
对于(12)(13)式子,运用引理3,可以得到
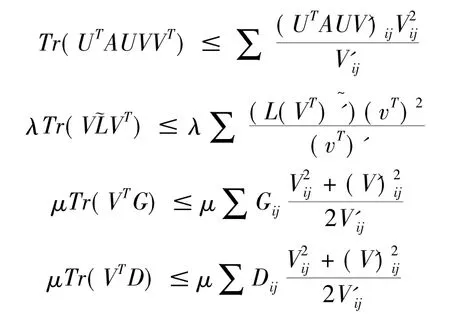
综上可得Z(V,V')≥O(V),因此Z(V,V')是O(V)的辅助函数.
为了得到Z(V,V')的极小值,求出其Hessian矩阵这里Yij是正定的对角矩阵,且
由Hessian矩阵性质知Z(V,V')是关于V的凸函数,用求导得到全局极小值.
[1]R.O.Duda,P.E.Hart,and D.G.Stork.Pattern classification [M].New York:John Wiley&Sons,2012.
[2]D.D.Lee and H.S.Seung.“Learning the parts of objects by nonnegative matrix factorization”[J].1999,401(6755):788-791.
[3]H.Liu,Z.Wu,X.Li,D.Cai,and T.S.Huang.“Constrained nonnegative matrix factorization for image representation”[J].Pattern A-nalysis and Machine Intelligence,IEEE Transactions on,2012,34(7): 1299-1311.
[4]W.Xu and Y.Gong.“Document clustering by concept factorization”[J].in Proceedings of the 27th annual international retrieval.ACM,2004:202-209.
(责任编辑:陈衍峰)
O152.5
A
1008-7974(2016)06-0031-03
10.13877/j.cnki.cn22-1284.2016.12.010
2016-05-12
辽宁省自然基金项目“大数据环境下高维视觉信息鲁棒表示方法研究”(60875029)
印爽,女,辽宁辽阳人,辽宁师范大学数学学院在读硕士.

