全面深化课程改革，践行数学核心素养

☉湖北恩施州教科院 杨超

全面深化课程改革，践行数学核心素养

☉湖北恩施州教科院 杨超

2014年3月，教育部印发了《关于全面深化课程改革，落实立德树人根本任务的意见》；教育部组织研究提出各学段学生发展核心素养体系；2016年9月正式发布了“中国学生发展核心素养”，以科学性、时代性和民族性为基本原则，以培养“全面发展的人”为核心，分为文化基础、自主发展、社会参与三个方面.数学学科六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析.2016年恩施州初中数学学业考试中许多试题源于教材又高于教材，具有灵活多变、旧题新出的特点，很好地践行了数学核心素养.本文以2016年恩施州初中毕业学业考试数学试题第24题为例进行评析.

一、试题欣赏

如图1，在矩形OABC纸片中，OA=7，OC=5，D为BC边上的动点，将△OCD沿OD折叠，当点C的对应点落在直线l：y=x-7上时，记为点E、F，当点的对应点落在边OA上时，记为点G．

（1）求点E、F的坐标.

（2）求经过G、E、F三点的抛物线的解析式.

（3）当点C的对应点落在直线l上时，求CD的长.

（4）在（2）中的抛物线上是否存在点P，使以E、F、P为顶点的三角形是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

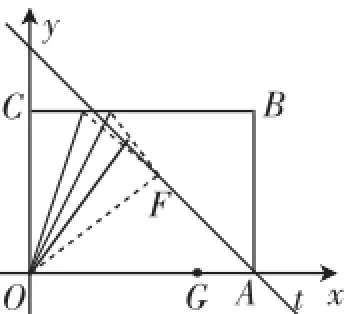
图1

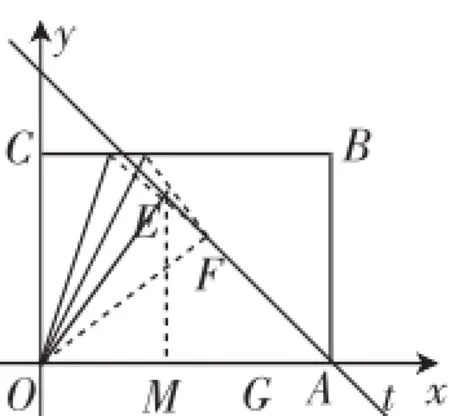
图2

标准答案：

解析：（1）如图2，过点E作EM⊥x轴于M.

由折叠知OE=OC=5.

设点E（x，-x+7），则EM=-x+7，OM=x.

在Rt△OME中，OM2+EM2=OE2.

则x2+（-x+7）2=52.

解得x=3或x=4.

当x=3时，y=-x+7=4；

当x=4时，y=-x+7=3.

则点E（3，4）、F（4，3）.

（2）设抛物线的解析式为y=ax2+bx+c.

由抛物线过点E（3，4）、F（4，3）、G（5，0），得

则所求抛物线的解析式为y=-x2+6x-5.

（3）如图3，当点C的对应点落在点E时，设CD=m，作ME⊥x轴于M，交BC于N.

由点E（3，4），得CN=3，EM=4，EN=5-4=1.

DN=3-m，DE=CD=m.

在Rt△DNE中，DE2=DN2+NE2.

即m2=（3-m）2+12.

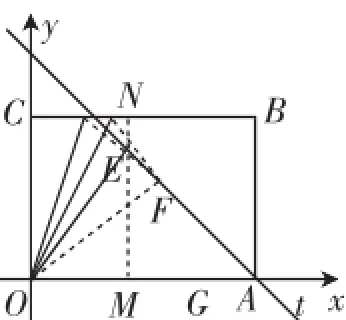
图3

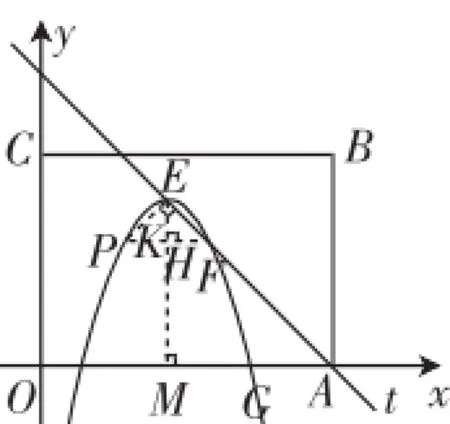
图4

（4）假设抛物线上存在点P符合题意，设点P（x，-x2+ 6x-5）.

若PF为斜边，如图4，作FH⊥EM于H，作PK⊥EM于K.

∠PKE=∠EHF=90°.又∠PEK=∠EFH，则△PKE∽△EHF.

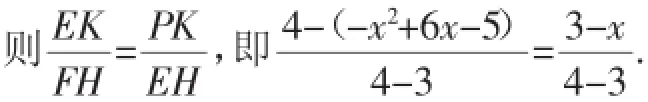
即x2-5x+6=0.

解得x=3（舍）或x=2，则点P（2，3）.

若PE为斜边，同理可求得P（1，0）.

若EF为斜边，点P在以EF为直径的圆上，显然该圆除点E、F以外与抛物线无交点，所以此时不存在点P使△EPF为直角三角形．

则存在点P（2，3）或点P（1，0），使以E、F、P为顶点的三角形为直角三角形．

二、试题评析

试题来源于新人教版八年级上册P79习题2和八年级下册数学活动折纸，以矩形的折叠为载体，要求学生从运动变化中探究不变的数学本质，动静结合，多个知识点交织在一起，综合运用了矩形、全等三角形、勾股定理、二次函数与一元二次方程、直线与圆等初高中衔接内容，题目设计循序渐进，梯度分明，综合性强.题目精心设计，构思巧妙，矩形的长是7，宽是5，精心设置这组数据是为了得出勾股数3、4，在此基础上生成3+4=7，为进一步求解奠基.动手操作，探索解题思路，多种方法都行得通，但难易程度相去甚远，要一下子捕捉到简单、自然的方法，快速求出结果，需要丰富的数学核心素养和解题经验.在数学思想方法方面，渗透了数形结合思想、函数思想、方程思想、转化思想及分类讨论思想等数学思想，考查学生的思维能力、计算能力，培养学生运动变化的辩证唯物主义观，是一道践行数学核心素养的好题.

三、践行数学核心素养——数学抽象、数学建模

对于此题，初读迷茫一片，如一头雾水：1.将△OCD沿OD折叠，点C的对应点C′落在直线l：y=-x+7上吗？要落在直线上，与什么量有关？取决于什么？2.点C′的位置是只有两个点吗？重重迷雾直指折叠后点C的对应点C′，抽象为数学问题就是动手实践中的“翻折”；在实践中把握问题实质，回到操作中去，定位C′.

引导学生动手操作：拿一张自备的矩形纸片，按图5所示方式折叠矩形的一个角，并使折痕经过O点.

教师提问：折叠时，你会遇到什么问题？在学生回答没告诉沿哪条折痕折叠时，教师追问：确实，本题没有给出折痕，正因为没给，所以同学们折的不一样，是完全不一样吗？在学生思考得出所有折叠都过O点时，教师鼓励学生进行反复不同的操作.在学生充分体验思考后，教师引导：过O点折叠矩形的一个角，你有什么感悟吗？如果你有感悟，能和同学分享一下吗？当有学生指出，过O点折叠矩形的一个角，实质上是把线段OC绕O点旋转时，教师适时给出引导：过O点任意折叠矩形的一个角时，C点必落在哪儿？此时学生易给出如下应答：C点必在以O为圆心，OC为半径的圆上，如图6所示.

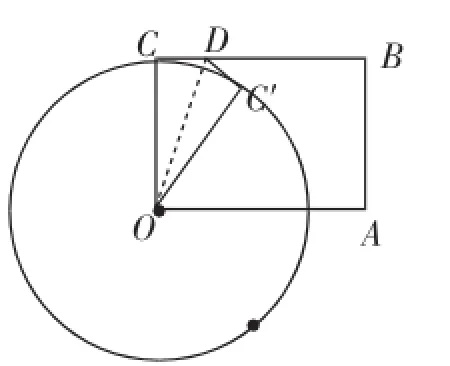
图6

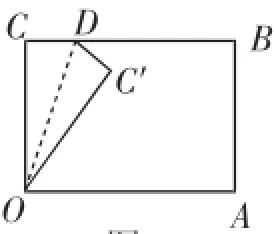
图5

观察并思考下列问题：

①过O点折叠矩形的一个角，C点一定会落在直线l上吗？

②过O点折叠矩形的一个角，C点所落的位置C′点与直线l有哪些位置关系？

③折叠后C点与直线l三种位置关系取决于什么？与哪些量有关？

不难发现，C点与l的关系，实质上就是直线与圆O的位置关系，而直线与圆的位置关系用圆心到直线的距离d与r（OC）的大小关系来衡量.这就回到了直线和圆的位置关系的数学模型.易求得圆心到直线的距离＜5，所以直线与圆有两个交点.令交点为E、F，如图7所示.

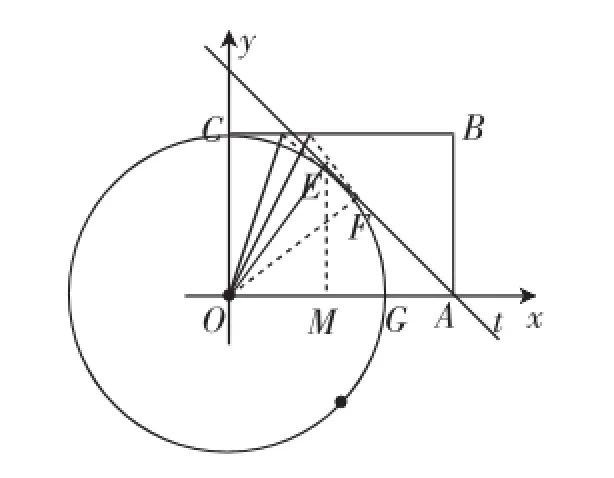
图7

如图7所示，定点E、F已经找到，那么AE、AF就一定是定值.

问题化归到定点E、F到矩形OABC的顶点、边界、静态线段的距离都是定值时.于是很容易将问题化归为图8中的问题：在矩形OABC中，沿过O点的某条直线折一个“拐”，使C点落在边MN上，同理，F点也演化为类似问题.

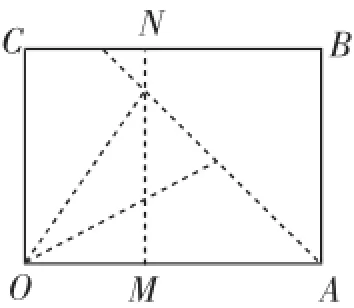
图8

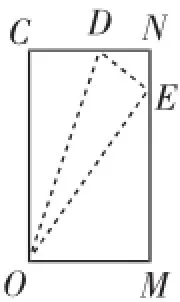
图9

找出图8中矩形OABC的有关已知线段.化繁为简，去掉多余的图形，从图8中提炼图9中的问题，在矩形OMNC中，沿直线OD折叠，D点恰好落在直线MN上的E点，且已知EN=1，求CD的长.怎样求DE的长呢？这时学生头脑中熟悉的翻折模型被唤醒了：将图形的一个角的顶点折到图形某边所在直线上，这里是将矩形的一个角“拐”的顶点折到相邻的边MN上，既然问题与熟知的模型有关，就得回到模型中去认识.转化到三角形中，用勾股定理模型求解.从而把几何问题转化为代数问题.

四、践行数学核心素养——直观想象、数学建模

在解答（4）时，除用标准答案外，可以通过数学建模、直观想象，简化运算，直接得出答案.要使以E、F、P为顶点的三角形是直角三角形，由分类讨论可分三类：

①以E为直角顶点.

如图10，作FH⊥EM于H，延长FH交抛物线于点P.由已知直观想象，显然三角形FHE为等腰直角三角形；∠FEH=45°.

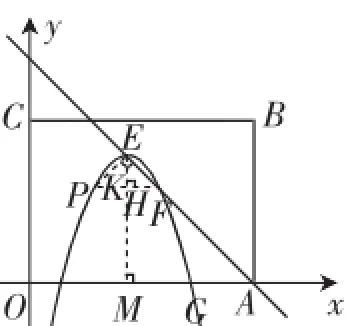
图10

由抛物线的对称性观察可得∠FEK=∠PEH=45°.

所以∠FEP=90°，显然点P满足条件.

点P与点F关于对称轴对称，由F（4，3），有P（2，3）.

②以F为直角顶点.

过F作FP⊥EF交抛物线于点P′.通过观察得P′（1，0）.

联想勾股定理模型.

由勾股定理可以求得：

FP′2=18，EF2=2，EP′2=20，显然FP′2+EF2=EP′2.

由由勾股定理逆定理知：

三角形P′EF为直角三角形.从而可求得P（1，0）.

③以P为直角顶点（同标准答案）.

这样通过直观想象、数学猜想、数学推理等，神奇.简洁地解决了数学难题，体现了数学的内在美.

五、践行数学核心素养——逻辑推理、数学运算、数据分析

题目构思巧妙，数据精心设计；题目中数据只有5、7，直线方程为x+y=7；由（1）的解答E（3，4）、F（4，3），数据中有3、4.经过数据分析、数学运算，3+4=7（x+y=7），32+ 42=52（x2+y2=52）.由直观想象、逻辑推理，有x、y对应3、4，所以x=3，y=4或x=4，y=3.由此可知E（3，4）、F（4，3）既在直线x+y=7上，又在以原点为圆心、5为半径的圆（x2+y2= 52）上.从而达到用最简洁的办法解决数学难题的目的.纵观此题题目和答案数据（1、2、3、4、5、7），仅有简单的6个个位数，却体现了数学的内在美，诠释了数学的魅力，令人叹为观止.

此题以平面直角坐标系为背景，通过翻折将全等变换、相似构造融进矩形中，数据设计非常巧妙.引导学生分析，构造基本图形.在解这类题时，首先要读懂图形，理解题意，深入挖掘隐含条件.要熟练掌握基础知识才能解决此问题.数学教学的精髓在于启发、引导学生探究、猜想、思考、受挫、反思、感悟的过程，在不断的参与中，穷尽问题本质，在理解和把握之后求解，是学生能力培养、品质提升的重要途径.在教学中，要强化核心知识的教学，引导学生探索问题的解决方法，教会学生思考，善于思考.全面培养学生的数学抽象、数学建模、直观想象、逻辑推理、数学运算、数据分析等核心素养，达到培养“全面发展的人”的核心目标.