一类分数阶微分方程边值问题解的存在性
蔡宁宁, 苏新卫, 张淑琴
(中国矿业大学(北京) 理学院 北京 100083)
一类分数阶微分方程边值问题解的存在性
蔡宁宁, 苏新卫, 张淑琴
(中国矿业大学(北京) 理学院 北京 100083)
将一类分数阶微分方程边值问题转化为等价的积分方程,通过构造特殊的Banach空间,应用Kuratowski非紧性测度的性质及Darbo不动点定理,得到了在无穷区间上分数阶微分方程解的存在性结果,并通过具体例子说明了主要结果.
分数阶微分方程; 边值问题; Banach空间; 非紧性测度
0 引言
近年来,分数阶微分方程由于在各个领域的广泛应用而备受关注[1],关于分数阶微分方程解的存在性和唯一性已经有了丰硕的成果[2-7].文献[8]讨论了一类分数阶微分方程边值问题:
(1)

(2)

1 预备知识
在下文中,用Dα、Dα-1表示α及α-1阶的Riemann-Liouville型分数阶导数,关于其定义和性质可参见文献[2].

定义空间
空间上的范数是
其中:0<ρi<1(i=1,2),易证,(X,‖·‖X)和(Y,‖·‖Y)是Banach空间.
引理1[3]若H⊂C(I,E)有界且等度连续,则α(H(t))在I上连续且
其中:H(t)={x(t):x∈H},t∈I.
引理2[3]设D是Banach空间E上有界闭凸子集,若算子T:D→D是严格集压缩,则T在D内有不动点.
2 主要结果
为应用Darbo不动点定理建立边值问题(2)解的存在性结果,假设f满足如下条件:
(H1) 存在非负函数a(t),b(t),c(t)∈C(J),0<ρi<1(i=1,2)使得
‖f(t,x,y)‖≤a(t)‖x‖ρ1+b(t)‖y‖ρ2+c(t),t∈J,x∈E,

(H2) 对于r1,r2>0,I⊂J,f(t,x,y)在I×BE(θ,r1)×BE(θ,r2)上一致连续,θ是E中零元,
(H3) 存在非负函数h(t)∈L1(J),使得α(f(t,S,Dα-1S))≤h(t)α(S),t∈J,其中S是E的有界子集,
引理3 若条件H1成立,则问题(2)等价于积分方程
证明过程参见文献[9]中引理3.1.
定义算子T:
则求解问题(2)转化为求算子的不动点问题.
引理4 若条件H1和H2成立,则算子T:Y→Y有界连续.
证明 第一步:T:Y→Y.对于∀u(t)∈Y,则u(t)∈X,注意到,
类似于文献[8]中引理3.2的证明,可得Tu(t)∈X.又
由f的连续性可得Dα-1Tu(t)∈C(J,E),且有
第二步:证明T:Y→Y有界.注意到上式以及




由Lebesgue控制收敛定理可得算子T的连续性.
引理5 若条件H1成立,B是Y的有界子集,则
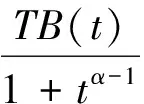
(b) 对∀ε>0,∃N>0使得对t1,t2≥N,u(t)∈B,有
证明 (a):由H1及B的有界性知存在K>0,使得对u∈B,
(3)
取R使得‖u(t)‖Y≤R,∀u∈B,令I=[a,b]⊂J为紧区间,t1,t2∈[a,b],t1 类似于文献[8]中引理3.3的证明易知:∃N1>0,对∀t1,t2≥N1, (4) (5) (6) 则对∀Tu1,Tu2∈TBi,t≥N,应用(4)和(5)式有 同理可得‖Dα-1Tu1(t)-Dα-1Tu2(t)‖ρ2≤(‖Dα-1Tu1(N)-Dα-1Tu2(N)‖+2ε)ρ2. 定理1 若条件H1~H3成立,则问题(2)至少存在一个解. 令B={u∈Y:‖u‖Y≤R},下证T:B→B.对∀u(t)∈B,有 当n→∞时,d(‖TnS(t)‖Y,‖TS(t)‖Y)→0,由非紧性测度性质得: 注意到(1+tα-1)ρ1>1,1/Γ(α)>1, 下面考虑问题(2)中u∞=0,且定理1中f的次线性条件改为超线性条件时,则有定理2. 定理2 若f满足(H0),存在非负函数a(t),b(t)∈C(J),ρi>1(i=1,2),使得 且同时满足H2和H3,则问题(2)至少存在一个解. (7) 显然f(t,x,y)∈C(J×E×E,E).注意到 (8) (9) 由(8)式可知 (10) 所以w={w1,w2,…,wn,…}∈E.由(8)和(10)式知,对∀ε1>0,∃n>N时,有 (11) 由(9)式知,对∀ε>0,∃K>0,使得当i>K时, (12) 由(11)和(12)式易得‖f(2)(t,x,y(m))-w‖≤ε,即当i→∞时,‖f(2)(t,x,y(m))-w‖→0.所以对D⊂E,f(2)(t,x,D)是相对紧集.故α(f(2)(t,x,D))=0.因此对任一有界集S⊂E,有 由定理1可知问题(7)至少存在一个解. [1] SABATIER J,AGRAWAL O P,TENREIRO M J A.Advances in fractional calculus[M].Nether-Lands:Springer,2007. [2] MA D X.Positive solutions of multi-point boundary value problem of fractional differential equation[J]. Arab journal of mathematical sciences,2015,21(2):225-236. [3] GUO D,LAKSHMIKANTHAM V,LIU X.Nonlinear integral equations in abstract space[M].Dordr-echt:Kluwer Academic Publishers,2013. [4] WANG J R,ZHANG Y.A class of nonlinear differential equations with fractional integrable impulses[J].Commun Nonlinear Sci Numer Simul,2014,19(9):3001-3010. [5] LIU Z H,LI X W.Existence and uniqueness of solutions for the nonlinear impulsive fractional differen-tial equation[J]. Communications in nonlinear science and numerical simulation,2013,18(6):1362-1373. [6] 王勇.非线性分数阶微分方程积分边值问题的正解[J].应用数学,2016,29(1):1-6. [7] 刘东利,杨军,崔更新.高阶分数阶微分方程边值问题正解的存在性[J].郑州大学学报(理学版), 2014,46(1):16-20. [8] SU X.Solutions to boundary value problem of fractional order on unbounded domains in a Banach space [J]. Nonlinear analysis,2011,74(8):2844-2852. [9] SU X,ZHANG S.Unbounded solutions to a boundary value problem of fractional order on the half-line[J]. Computers and mathematics with applications,2011,61(4):1079-1087. (责任编辑:王海科) Existence of Solutions to a Boundary Value Problem of Fractional Differential Equations CAI Ningning, SU Xinwei, ZHANG Shuqin (DepartmentofMathematics,ChinaUniversityofMiningandTechnology,Beijing100083,China) The existence of solutions to a boundary value problem of fractional differential equations on the half-axis in a Banach space was studied.The boundary value problem was transformed into an equivalent integral equation. By the properties of the Kuratowski noncompactness measure and Darbo’s fixed point theorem, the existence of solutions of boundary value problem were proved. An example illustrating the main result was also given. fractional differential equation; boundary value problem; Banach space; noncompactness measure 2016-07-25 国家自然科学基金项目(11371364). 蔡宁宁(1991—),女,河北邯郸人,硕士研究生,主要从事分数阶微分方程理论研究,E-mail:kuangdacnn@163.com. O175.8 A 1671-6841(2017)02-0007-07 10.13705/j.issn.1671-6841.2016210

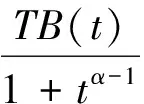

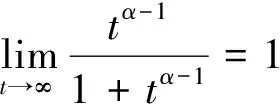



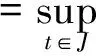
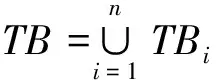
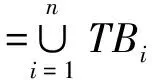


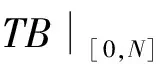










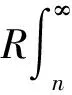




3 例子