谈“对数形结合思想方法”的感悟——以近三年高考压轴题为例

☉湖南省永顺县第一中学 石家文

谈“对数形结合思想方法”的感悟
——以近三年高考压轴题为例

☉湖南省永顺县第一中学 石家文

解决数学问题离不开数学思想方法，数学思想方法在解决数学问题时的作用举足轻重，思想方法选择得当，往往有事伴功倍的效果，思想方法不当，往往引起思维混乱，解题思路受阻.纵观近几年的高考试题，特别是函数压轴大题，有的以其复杂的分类讨论而令人生畏；有的因入口难寻而让人却步.其实，处理这类题数形结合是最有效的方法之一.下面笔者以近三年的高考压轴大题为例谈一谈“对数形结合思想方法”的感悟.

感悟之一：数形结合是避开分类讨论的最佳方法

例1（2016年全国高考理科卷21题）已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.

（1）若f（x）有两个零点，求a的取值范围.

（2）略.

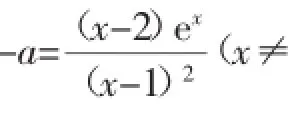
解：（1）由f（x）=0⇒a（x-1）2=（2-x）ex.

则f（x）有两个零点⇒直线y=-a与函数y=g（x）的图像有两个交点.

所以函数g（x）在（-∞，1）内单调递减，在（1，+∞）内单调递增.

当x≥2时，g（x）≥0，当x＜2时，g（x）＜0.

又g（0）=-2，故在同一坐标系中作直线y=-a及函数y=g（x）的图像，如图1所示.

由图1知，当且仅当-a＜0，即a＞0时，直线y=-a与函数y=g（x）的图像有两个交点.

故a的取值范围为（0，+∞）.

图1

反思：本题采用先分离参数再“数形结合”的方法将函数的零点画出来，让人一眼就能看出问题的答案，确实比评分标准上给的答案简单得多.一个图形胜过千言万语，它避开了复杂的分类讨论！

感悟之二：数形结合是撬开分类讨论入口的杠杆

（1）当a为何值时，x轴为曲线y=f（x）的切线；

（2）用min｛m，n｝表示m、n中的最小值，设函数h（x）= min｛f（x），g（x）｝（x＞0），讨论h（x）零点的个数.

分析：这是一道见过多次的新定义函数问题，一般方法先由不等式f（x）≤g（x）解出x的取值范围，然后将h（x）转化成分段函数，但是f（x）的表达式含有参数，且g（x）为超越式，故f（x）≤g（x）不可解（因为关于x的方程f（x）=g（x）的根算不出来），注意到函数g（x）=-lnx的图像易作出来，于是，解法如下.

解：（1）略.

图2

（2）由函数y=g（x）的图像（如图2）知，当x＜1时，g（x）＜0，当x=1时，g（x）=0，当0＜x＜1时，g（x）＞0，结合h（x）的定义知，有如下三种情况.

（1）当x∈（1，+∞）时，g（x）=-lnx＜0，h（x）=min｛f（x），g（x）｝≤g（x）＜0，h（x）在（1，+∞）内无零点.

（3）当x∈（0，1）时，g（x）=-lnx＞0，由h（x）的定义知，若（fx）=0，则x就是h（x）的零点，故只需研究（fx）在（0，1）内的零点个数.

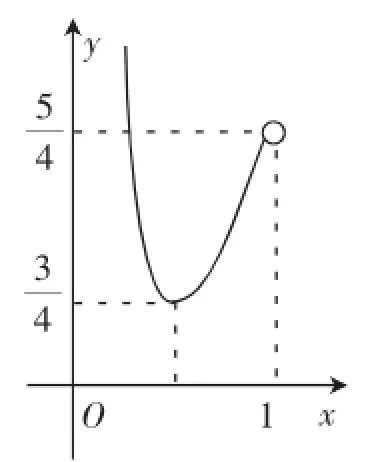
图3

1 x=-a有一个解，所以（fx）在（0，1）内仅有一个零点；

反思：本题当年参加高考的学生普遍反映难度太大，难以入手，由于参数无法分离，不能像例1那样画图解决，但是，上述解法充分利用了函数g（x）=-lnx的图像特点，结合h（x）的定义及函数零点的几何意义，自然而然分三类讨论，转化研究函数t（x）的零点个数.

以上解法，关键是通过研究函数图像，采用数形结合的方法，找到了分类讨论的入口和分类标准，使问题圆满解决.数形结合的确像一根杠杆，发挥了四两拨千斤的功效.

感悟三：数缺形时少直观，形缺数时难入微

例3（2014年天津高考理科卷20题）设（fx）=x-aex（a∈R），x∈R，已知函数y=（fx）有两个零点x1，x2，且x1＜x2.

（1）求a的取值范围；

（3）略.

原供参考解答如下：

解析：（1）由（fx）=x-aex，可得f（′x）=1-aex.

下面分两种情况讨论：

（i）a≤0时，f（′x）＞0在R上恒成立，可得（fx）在R上单调递增，不合题意.

（ii）a＞0时，由f（′x）=0，得x=-lna.

当x变化时，f（′x），（fx）的变化情况如下表：

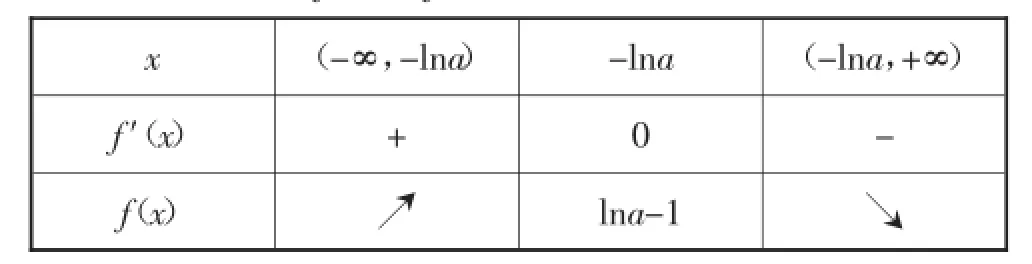
这时，f（x）的单调递增区间是（-∞，-lna）；单调递减区间是（-lna，+∞），于是，“函数y=f（x）有两个零点”等价于如下条件同时成立：

①f（-lna）＞0；

②存在s1∈（-∞，-lna），满足f（s1）＜0；

③存在s2∈（-lna，+∞），满足f（s2）＜0.

由f（-lna）＞0，即-lna-1＞0，解得0＜a＜e-1.

而此时，取s1=0，满足s1∈（-∞，-lna），且f（s1）=-a＜0；

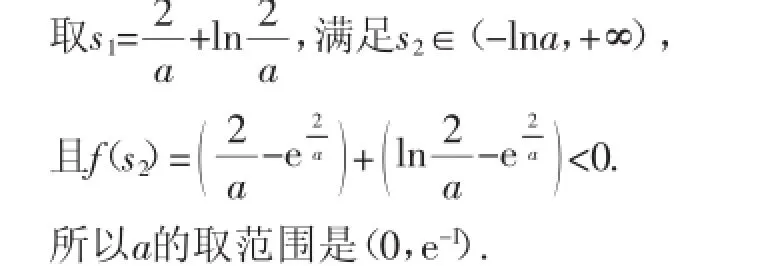
并且，当x∈（-∞，0）时，g（x）≤0；当x∈（0，+∞）时，g（x）＞0.

由已知，x1，x2满足a=g（x1），a=g（x2）.

由a∈（0，e-1）及g（x）的单调性，可得x1∈（0，1），x2∈（1，+∞）.

对于任意的a1，a2∈（0，e-1），设a1＞a2，g（ξ1）=g（ξ2）=a1，其中0＜ξ1＜1＜ξ2；g（η1）=g（η2）=a2，其中0＜η1＜1＜η2.

因为g（x）在（0，1）上单调递增，故由a1＞a2，即g（ξ1）＞g（η1），可得ξ1＞η1；类似可得ξ2＜η2.

说明：暂且不说第（1）问的解法是否简单，上述对第（2）问的证明笔者花一个多小时尚未看出究竟.于是，笔者按自己的思路从第（1）问做起，解答如下：

由g′（x）≥0⇒x≤1，所以函数g（x）在（-∞，1］内单调递增，在［1，+∞）内单调递减.

又当x≤0时，g（x）≤0；当x＞0时，g（x）＞0.

在同一坐标系中，作出直线y=a及y=g（x）的图像，如图4所示.

又f（x）有两个零点⇒直线y=a与函数y=g（x）的图像有2个交点.

反思：在笔者用分离参数和数形结合的方法轻松解决第（1）问之后，再来解决第（2）问，由图4作出图5后，笔者顿时恍然大悟：

原供第（2）问的解答就在图中.笔者深深地体会到：数缺形时少直观啊！于是第（2）问的证明如下：

图4

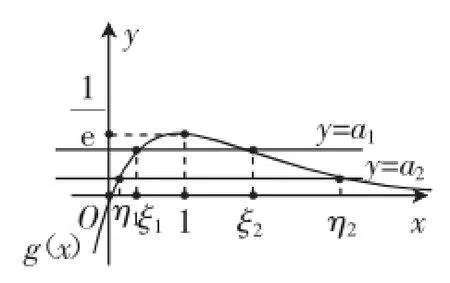
图5

（2）由图5可以知，当a的取值由a1减小到a2时对应值由明显增大.

反思：第（2）问的证明真的如此简单？“可以看图说话，不能以图代证，必须用代数方法来论证”，因此，上述对第（2）问的证明是不严谨的.究竟该如何证明呢？这种一眼就能看出的结论偏偏就是讲不出道理的经历，使笔者深深体会到“形缺数时难入微”.

感悟之四：数形结合千般好，隔离分家万事休

上述例3的第（2）问如何证明呢？经过对图5认真观察：发现函数g（x）在（0，1］上递增，在［1，+∞）上递减，这一直观发现，让第（2）问的证明水到渠成.

反思：以形助数是发挥图形的直观性，使抽象的东西具体化；而以数辅形是用数式的严谨性来弥补形的不足，由于数缺形时少直观，形缺数时难入微，因此只有数与形相结合，发挥两方面的优势，才能形成互补，相得益彰.

综上所述，数学解题中要善于发掘“数”与“形”的内在联系，借助图形的直观性和数式的严谨性，去揭示和描述数学问题的本质.借助图形的直观性，有时可以避开分类讨论；有时可以找到分类讨论的标准和入口；有时可以揭示题中的隐含条件，从而迅速找到解题途径，达到以形助数的目的.然而，对于代数证明，即使由图可以直观看出答案，也不能以图代证，需借助数式的严谨性，采取以数辅形、数形结合的方法，发挥两方面的优势，形成互补.

总之，数学解题首先要有扎实的数学基本知识和基本技能，并在此基础上进一步发展成为基本思想方法.著名教育家张奠宙教授说：“数学思想是对数学的本质认识，是对数学事实与理论进行抽象概括的认识的升华，数与形是数学中最基本的研究对象，数形结合是最重要的数学思想.”我国伟大数学家华罗庚先生也曾说过：“数缺形时少直观，形缺数时难入微，数形结合千般好，隔离分家万事休.”因此，解题时若能巧妙应用数形结合思想，“由数思形，以形助数”或“由形思数，以数辅形”，发挥数与形的双重优势，往往能在短时间内化简解题过程，培养思维的灵活性，提升解题能力.

1.石家文.例谈函数零点问题解题策略［J］.湖南教育，2016（10）.F