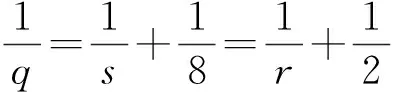带加性噪声的分数阶随机Ginzburg-Landau方程的渐近行为
王云肖,舒 级,杨 袁,李 倩,汪春江
(四川师范大学 数学与软件科学学院,四川 成都 610066)
带加性噪声的分数阶随机Ginzburg-Landau方程的渐近行为
王云肖,舒 级*,杨 袁,李 倩,汪春江
(四川师范大学 数学与软件科学学院,四川 成都 610066)
考虑带加性噪声的随机分数阶Ginzburg-Landau方程在L2(D)中的渐近性质.首先将随机偏微分方程转化为仅含随机参数的随机方程,然后对该方程的解进行先验估计,从而得到随机动力系统的紧性,最后证明L2(D)中随机吸引子的存在性.
随机分数阶Ginzburg-Landau方程; 随机动力系统; 随机吸引子; 加性噪声
复Ginzburg-Landau方程是关于非平衡流体动力系统和化学系统的不稳定、超导和超流体、非线性光纤和Bose-Einstein凝聚及其空间模型描述的重要模型.它是一个非常有趣的模型.非线性Schrödinger方程是一Hamilton系统,在有限时间拥有局部奇异解,复Ginzburg-Landau方程是非线性Schrödinger方程的耗散情形.目前有许多关于Ginzburg-Landau方程的研究[1-9].Guo B.L.等[9]研究了广义2D Ginzburg-Landau方程
并得到了在
条件下整体吸引子的存在性.对于随机情形,文献[10]研究了随机广义2D Ginzburg-Landau方程
本文考虑如下带加性噪声的随机广义2D分数阶Ginzburg-Landau方程
(1)
具有周期边界条件和初始条件:
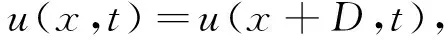
(2)
其中,u(x,t,ω)是未知复值函数,x∈D=[0,1]×[0,1],t>0,ω∈Ω,(-△)α是分数阶拉普拉斯算子,Φ是线性算子,ρ>0,1<α<2,γ,μ,β是实参数,λ1和λ2是复参数.W是关于时间的双边柱形Wiener过程,它是定义在适应于{Ft}t≥0的完备概率空间(Ω,F,P)中的取值于L2(0,1)上的函数,可写为
其中,wk(k∈N)是相互独立的Brown序列,(ek)k∈N是L2(D)上的正交基.
令Ω={ω∈C(R,U)|ω(0)=0},其中U是一个Hilbert空间并且满足L2(D)U是Hilbert-Schmidt嵌入的,则W(t)是取值于U的随机过程,且其对应的随机变量属于C(R,U).Φ是L2(D)上的有界线性算子.
本文的目的是证明问题(1)和(2)在L2(D)上存在随机吸引子.为此,需要证明u(t)关于时间在不同空间的一致有界性.本文应用类似于文献[11-14]中的方法来解决这个问题.
1 预备知识
首先给出随机动力系统的一些相关知识[15-16].若(Ω,F,P)是一个概率空间,{θ:Ω→Ω},t∈R+是一簇保测度变换,并且映射(t,ω)|→θtω是可测的,θ0=IX,θt+s=θtθs,其中,s,t∈R,则(θt)t∈T是一个流,((Ω,F,P),(θt)t∈T)是一个可测动力系.
定义 1.1 设(X,d)是可分的距离空间,F是Borelσ-代数,θt是(Ω,F,P)对应的保测度变换,若可测映射
在X上满足:
1)S(0,ω)=IX,
2) 对任意的s,t∈R,ω∈Ω,有S(t+s,ω)=S(t,θsω)∘S(s,ω),其中∘代表复合算子,
3)S(t,ω):X→X是连续的;
那么称S是一个连续随机动力系统.
定义 1.2 给定一个随机集K,集合
称为K的Ω-极限集.
定义 1.3 若S是随机动力系统,存在随机紧集ω|→A(ω)满足以下条件:
1)A(ω)是严格不变的,即对于所有t>0,S(t,ω)A(ω)=A(θtω),
2)A(ω)吸引所有确定有界集B⊂X;
那么称A(ω)为S的随机吸引子.
定理 1.1 假设S是Polish空间上的随机动力系统,若存在紧集ω|→K(ω)吸收每一个有界非随机集B∈X,那么集合
是S的随机吸引子.
接下来给出交换子估计的相关引理[17].
引理 1.1 设u∈Lq并且对于u的m阶导数为Dmu∈Lr,1≤q,r≤∞.对于Dju,0≤j (3) 并有 (4) 引理 1.2 假设S>0并且p,p2,p3∈(1,∞).如果f,g∈S,并且 (5) 则有不等式 (6) 下面给出分数阶拉普拉斯算子和分数阶Sobolev空间及其范数的定义[18]. 另外,分数阶Sobolev空间Hα的范数规定如下 本文常用的几个函数空间定义如下 其范数分别记为‖·‖和‖·‖V. 下面证明问题(1)和(2)随机动力系统的存在性.为此,方程(1)可写为 (7) Φ:L2(D)→D是线性算子.引入如下带初值的线性方程 初始条件为z(0)=0.该方程的解z是Ornstein-Uhlenbeck过程,z∈C([0,∞],V)[13],z是稳态遍历过程,它的迹是P-a.s.连续的,并且对于任意t和s有 设B是H中的有界集,对于t0<0和u(t0)∈B,令 其中,u是方程(1)的解.由方程(7)和v的形式知,随机过程v满足随机方程 (8) (9) 对于P-a.s.ω∈Ω,v0∈L2(D),存在唯一解v∈C1((0,T):H)∩C([0,T):H),∀T<∞,且对于t≥t0,映照ξ=v(t0)|→v(t)从H到V是连续的. 对任意v(t0)=v0,v(t,ω;t0,v0)表示方程(8)和(9)的解有 显然,由 定义了随机动力系统{(S(t,ω;t0))}t≥t0,ω∈Ω,称为由带加性噪声的随机分数阶Ginzburg-Landau方程产生的流.对于t≥t0,映照ω→S(t,ω;t0)u0是可测的. 现证明{(S(t,ω;t0))}t≥t0,ω∈Ω是紧的,并且t=0时在H、V中存在紧吸收集.令v是方程(8)和(9)的解,对于ω∈Ω,需要得到解v在H、V上的先验估计.在本文中,εi(i=1,2,…,13),i(i=1,2,…,8),ki(i=1,2,…,8),κi(i=1,2,…,14),C和c表示依赖方程(1)系数的正常数. 证明 将方程(8)与v作内积,并取实部得 (10) 首先有 (11) (10)式右边第1项可估计为 (12) (10)式右边第2和第3项分别估计为 (13) 和 (14) 通过(10)~(14)式得到 (15) 其中 且 (16) 通过(15)和(16)式可得到 且 那么可得 根据Gronwall不等式有 在t→-∞时,ω∈ω,g3(t)≥0,P-a.s,至多以多项式增长,即r1是P-a.s.有限的[11]. 引理 3.2 不等式 成立,且g5(t)证明过程中给出. 证明 将方程(8)与|v|6v作内积,并取实部得 (17) 注意到 (18) (17)式左边为 (19) (17)式右边第2项可估计为 对任意ε有0<ε<α并且p<∞且1/p+1/q=1,令ε=1/p得到 (20) 方程(17)等号右边第3项可以估计为 (21) 方程(17)等号右边第4项估计为 (22) 注意到 其中,在1 (22)式右边第1项可估计为 (22)式右边第2项可估计为 (22)式右边第3项可被估计为: 和 由上式,(22)式可估计为 (23) 其中 且 因为 求得 同上可得 (24) 由(18)~(25)式,(17)式可变为 其中 得证. 证明 将方程(8)与(-△)αv作内积,并取实部得 (26) 注意到 (27) (26)式右边第1项展开可得 (28) 且 (29) 因为 (30) 由(28)~(30)式可估计为 (31) 其中 (26)式右边第2项和第3项,可分别估计为 和 且 (32) 其中 通过(26)~(32)式,(26)式可变为 (33) 其中 根据(33)式和引理3.2可得 其中 使得 上式的积分是一个二次型,若其矩阵M为非负定的,则有 (34) 则二次型也是非负定的,于是积分为非正. 注意到 (35) 即 (37) 且 (38) 根据(34)~(38)式得 (39) 则 有 (40) g8(t)≥0(t→∞)至多以多项式增长,即r2是P-a.s.有限的. 定理 3.1 带附加噪声的随即广义2D分数阶Ginzburg-Landau方程的随机流{(S(t,s;ω))}t≥s,ω∈Ω,在H中存在紧的吸引子. 证明 由引理1.2和3.3可得该随机动力系统在H、V中存在吸收集,又嵌入VH在区域D上是紧的,因此由定理1.1便得定理3.1. [1] DOERING C,GIBBON J D,HOLM D.Low-dimensional behavior in the complex Ginzburg-Landauequation[J].Nonlinearity,1988,1(2):279-309. [2] GHIDAGLIA J M,HERON B.Dimension of the attractor associated to the Ginzburg-Landau equation[J].Physica:Nonlinear Phenomena,1987,D28(3):282-304. [3] BARTUCCELLI M,CONSTANTIN P,DOERING C.On the possibility of soft and hard turbulence in the complex Ginzburg-Landau equation[J].Physica:Nonlinear Phenomena,1990,D44(3):421-444. [4] DOERING C R,GIBBON J D,LEVERMORE C D.Weak and strong solutions of the complex Ginzburg-Landau equation[J].Physica:Nonlinear Phenomena,1994,D71(3):285-318. [5] LEVERMORE C D,OLIVER M.The Complex Ginzburg-Landau Equation as a Model Problem[M].Providence:American Mathematical Society,1997. [6] BATUCCELLI M,GIBBON J D,OLIVER M.Lengths scales in solutions of the complex Ginzburg-Landau equation[J].Physica:Nonlinear Phenomena,1996,D89(3):267-286. [7] LI D L,GUO B L.On Cauchy problem for generalized complex Ginzburg-Landau equation in three dimensions[J].Progress in Natural Science,2003,13(9):658-665. [8] LI D L,DAI Z D.Long time behavior of solution for generalized Ginzburg-Landau equation[J].J Math Anal Appl,2007,330(2):934-948. [9] GUO B L,WANG X.Finite dimensional behavior for the derivative Ginzburg-Landau equation in two spatial dimensions[J].Physica:Nonlinear Phenomena,1995,D89(1):83-99. [10] HONG L,SHU J L.Random attractor for fractional Ginzburg-Landau equation with multiplicative noise[J].Taiwanese J Math,2014,2(18):435-450. [11] 李栋龙,郭柏灵.带附加噪声的随机广义2D Ginzburg-Landau 方程的渐进行为[J].应用数学和力学,2009,30(8):883-894. [12] CRAUEL H,FLANDOLI F.Attractors for random dynamical systems[J].Probability Theory and Related Fields,1994,100(3):365-393. [13] CRAUEL H,DEBUSSCHE A,FLANDOLI F.Random attractors[J].J Dyn Diff Eqns,1997,9(2):307-341. [14] ARNOLD L.Random Dynamical Systems[M].New York:Springer-Verlag,1998. [15] PRATO G D,ZABEZYK J.Stochastic equations in infinite dimension[C]//Encyclopedia of Mathematics and Its Applications.Cambridge:Cambridge University Press,1992. [16] TARASOV V E,ZASLAVSKY G M.Fractional Ginzburg-Landau equation for fractal media[J].Physica:Statistical Mechanics and its Applications,2005,A354:249-261. [17] PU X K,GUO B L.Well-posedness and dynamics for the fractional Ginzburg-Landau equation[J].Appl Anal,2013,92(2):318-334. [18] 郭柏灵,蒲学科,黄凤辉.分数阶偏微分方程及其数值解[M].北京:科学出版社,2015. 2010 MSC:35Q56; 60H15 (编辑 李德华) Asymptotic Behavior of the 2D Generalized Fractional Stochastic Ginzburg-Landau Equation with Additive Noise WANG Yunxiao,SHU JI,YANG Yuan,LI Qian,WANG Chunjiang (CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan) In this paper,the asymptotic dynamic problem is considered for the fractional stochastic Ginzburg-Landau equation with additive noise defined inL2(D).Firstly,the partial differential equation is trasformed into the random equation that only includes the random parameters.The compactness of the random dynamical system then is established by a priori estimation method.And finally,the existence of a random attractor for the random dynamical system is proved inL2(D). stochastic fractional Ginzburg-Landau equation; random dynamical system; random attractor; additive noise 2016-04-13 四川省科技厅应用基础计划项目(2016JY0204)和四川省教育厅自然科学重点科研基金(14ZA0031) O177.92 A 1001-8395(2017)02-0149-08 10.3969/j.issn.1001-8395.2017.02.002 *通信作者简介:舒 级(1977—),男,副教授,主要从事随机动力系统和偏微分方程的研究,E-mail:shuji2008@hotmail.com
2 随机分数阶Ginzburg-Landau方程的解及其对应的随机动力系统
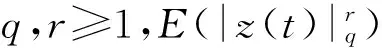
3 随机吸引子的存在性