带有一阶导数的脉冲微分方程多点边值问题解的存在性

李海艳,李军燕,李利玫

(1.四川大学 锦城学院,四川 成都 611731;2.四川师范大学 数学与软件科学学院,四川 成都 610066)

带有一阶导数的脉冲微分方程多点边值问题解的存在性

李海艳1,李军燕1,李利玫2

(1.四川大学 锦城学院,四川 成都 611731;2.四川师范大学 数学与软件科学学院,四川 成都 610066)

利用Leray-Schauder不动点定理讨论一类非线性项与一阶导数有关的二阶脉冲微分方程的多点边值问题,将以往所研究的方程的脉冲项和边界条件作了改进,得到了解的存在性新结果.

Banach空间; 多点脉冲微分方程; 边值问题; Leray-Schauder不动点定理

1 预备知识

脉冲微分方程是研究过程状态发生突然变化动力学的基本工具,反映了微分方程在固定或不固定时刻的瞬时改变,因此能更真实广泛地描述自然界性态.这一特点日益引起人们的重视,并将其广泛应用于生物、医疗、社会、经济、工程、物理、航空航天等诸多领域的研究[1-2].随着人类的不断进步与探究,脉冲微分方程方面的数学理论取得了重大进展,特别是边值问题的研究愈来愈引起数学家们的重视,并有了非常丰富的研究成果,其中不乏多点边值问题的讨论[3-10].然而,带有脉冲的边值问题的研究[11-19]也逐渐成为一些学者研究的一个焦点,但是对带有脉冲的多点边值问题的研究[11-12]甚少.

文献[10]利用Krasnoselskii不动点定理讨论了如下多点边值问题正解的存在性:

对于脉冲微分方程,文献[11]研究了只含有导数脉冲的多点边值问题

其中,J=[0,1],f∈C(J×R+,R+),Ik∈C(R+,R+),0<ξ1<ξ2<…<ξm-2<1,ai,bi∈(0,+∞),i=1,2,…,m-2.应用锥上的不动点定理获得了多个正解的存在性定理.

受文献[10-11]的启发,本文讨论了如下的二阶脉冲微分方程的m-点边值问题(BVP)

(1)

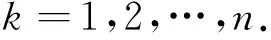
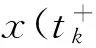
本文对文献[10-11]所研究的方程的脉冲项做了改进,对其边界条件进行了修改,并且在非线性项含有一阶导数的情形下运用Leray-Schauder不动点定理获得了该类问题解的存在性定理.

2 主要引理及其证明

显然,PC[J,R]在‖·‖PC下构成一个Banach空间,PC1[J,R]在‖·‖下构成一个Banach空间.

(2)

证明 设x是BVP(1)的解,对(1)式两端积分

(3)

对(3)式再次积分得

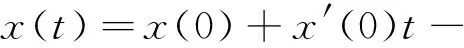
(4)

在(4)式中分别令t=1,t=ξi,则有

结合边值条件有

即

所以

再结合(4)式可得(2)式.

反过来,假定x∈PC1[J,R]是脉冲微分方程(2)的解,易知

当t≠tk时,直接对(2)式求二阶导数可得

和

故x∈PC1[J,R]∩C2(J′),可以验证

定义算子T:PC1[J,R]→PC1[J,R]如下

引理 2.2[20]集合H⊂PC1(J,R)是相对紧集的充分必要条件为H中的诸函数x(t)及其导函数x′(t)都在J上一致有界且在每个Jk(k=1,2,…,m)上等度连续.

由引理2.1和引理2.2可得引理2.3.

引理 2.3 算子T是从PC1(J,R)到PC1(J,R)的全连续算子.

引理 2.4[20](Leray-Schauder定理) 设X为实Banach空间,算子T:X→X为全连续算子,若集合{‖x‖|x∈X,x=λTx,0<λ<1}是有界的,则方程x=Tx至少有一个解.

3 存在性结果

定理 3.1 假设下列条件成立:

(H2) 存在常数M≥0,使得

(H3) 存在非负常数τk>0,ηk>0,使得

且

(H4) 存在常数βk>0,使得

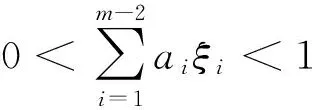
那么BVP(1)至少有一个解.

证明 由引理2.4可知,只需要证明方程

(5)

的解集在PC1(J,R)中有一个不依赖于λ的先验界.

对∀t∈J,由

可得

则

因为

所以

由此可知,只要‖x′‖有界,则‖x‖也有界.

接下来验证‖x′‖的有界性.

为了计算方便,令x(t)=λ[x1(t)+I(t)],其中:

则有

当0≤t≤ξ1时

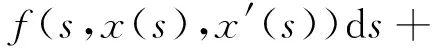
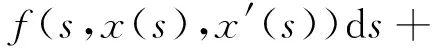
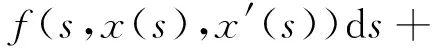
当ξr-1≤t≤ξr,2≤r≤m-2时

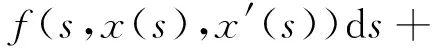
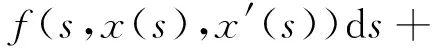
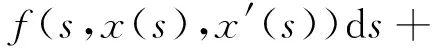
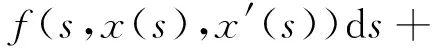
当ξm-2≤t≤1时

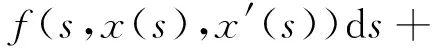
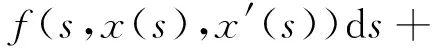
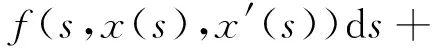
综上,当0≤t≤1,ξi-1≤s≤min{ξi,t}时

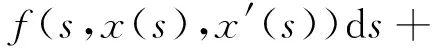
当0≤t≤1,max{ξi-1,t}≤s≤ξi时

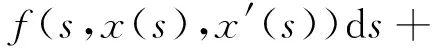
由上述讨论可知,当ξi-1≤s≤min{ξi,t}时

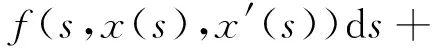
由(H1)可得

将上式中的s换成tk不等式也成立,从而可得

当max{ξi-1,t}≤s≤ξi时

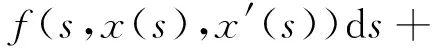
同理,由(H1)可得

将上式中的s换成tk不等式也成立,从而也可得

经过以上分析得

(6)

又已知

即

(7)

由(6)和(7)式得

(8)

由条件(H5),存在ε>0,满足

由(H2),对上述ε>0,存在N>0,使得当0≤t≤1,‖x‖+‖y‖>N时有

从而

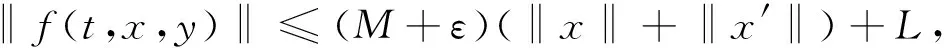
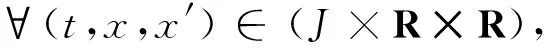
(9)

其中

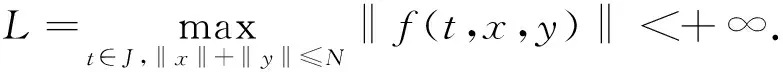
类似地,由(H4),对上述ε>0,存在Nk>0,k=1,2,…,n,使得当0≤t≤1,‖x‖+‖y‖>Nk时有

从而

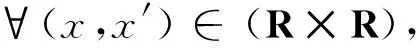
(10)

其中

现在,由(H3)以及(8)和(9)式可得

为了方便,引入记号

结合以上分析,易得对于∀0<λ<1,都有

因此,‖x′‖有界,可得‖x‖也有界.故定理3.1得证.

[1] NENOV S.Impulsive controllability and optimization problems in population dynamics[J].Nonlinear Analysis:TMA,1999,36(7):881-890.

[2] KELLEY W G,PETERSON A C.Difference Equations:an Introduction with Applications[M].New York:Academic Press,1991.

[3] ZHANG G W,SUN J X.Positive solutions ofm-point boundary value problems[J].J Math Anal Appl,2004,291:406-418.

[4] JIANG W H,GUO Y P.Multiple positive solutions for second-orderm-point boundary value problems[J].J Math Anal Appl,2007,327:415-424.

[5] JIANG W H.The existence of positive solutions for second-order multi-point BVPs with the first derivative[J].Comput Math Appl,2009,225:387-392.

[6] WEI L,LIU Y X.Study on a kind of nonlinear neumann boundary value problems[J].Math Appl,2015,28(1):99-109.

[7] WEI L,LIU Y X.Research on the existence of solution of generalized curvature boundary value problems[J].Acta Math Scientia,2014,34(4):938-947.

[8] 李萍,舒级,张佳,等.一个具有相互作用非线性项的分数阶微分方程组的爆破解[J].四川师范大学学报(自然科学版),2016,39(1):15-19.

[9] 涂馨予,蒲志林.一类带一般记忆核的Cahn-Hilliard方程解的能量衰减估计[J].四川师范大学学报(自然科学版),2016,39(1):20-25.

[10] SUN Y P.Positive solutions of nonlinear second-orderm-point boundary value problem[J].Nonlinear Analysis,2005,61:1283-1294.

[11] FENG M Q,XIE D X.Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations[J].J Comput Appl Math,2009,223:438-448.

[12] LIU B,YU J S.Existence of solution for m-point boundary value problems of second-order differential systems with impulses[J].Appl Math Comput,2002,125:155-175.

[13] 魏君,蒋达清,祖力.一维p-Laplace二阶脉冲微分方程的奇异边值问题[J].应用数学学报,2013,36:414-430.

[14] 李耀红,张晓燕.Banach 空间中一类二阶非线性脉冲积分-微分方程边值问题解的存在性[J].应用数学,2011,24(1):112-119.

[15] YAO M P,ZHAO A M,YAN J R.Anti-periodic boundary value problems of second order impulsive differential equations[J].Comput Math Appl,2010,59:3617-3629.

[16] YAO M P,ZHAO A M,YAN J R.Periodic boundary value problems of second-order impulsive differential equations[J].Nonlinear Analysis,2009,70:262-273.

[17] TIAN Y,JIANG D Q,GE W G.Multiple positive solutions of periodic boundary value problems for second order impulsive differential equations[J].Appl Math Comput,2008,200:123-132.

[18] ZHANG L L,ZHAI C B.Existence and uniqueness of positive solutions to nonlinear second order impulsive differential equations with concave or convex nonlinearities[J].Discrete Dyn Nat Society,2013,2013:1-11.

[19] JIANG W H,ZHANG Q,GUO W W.Multiple positive solutions for second order impulsive differential equation[J].Electron J Qual Theory Diff Eqns,2013(6):1-11.

[20] 郭大均.非线性分析[M].济南:山东科技出版社,2001.

2010 MSC：34B10; 34B37

(编辑 李德华)

The Existence of Solutions for Multi-point Boundary Value Problem of Impulsive Differential Equations with the First Derivative

LI Haiyan1,LI Junyan1,LI Limei2

(1.DepartmentofMathematics,CollegeofJincheng,SichuanUniversity,Chengdu611731,Sichuan;2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

This paper studies the existence of solutions for multi-point boundary value problem of second-order impulsive differential equations with the first derivative.The boundary value conditions and impulsive term are extended.By using Leray-Schauder fixed-point theorem,the new conclusions about the existence of the solution are obtained.

Banach space; multi-point impulsive differential equation; boundary value problem; Leray-Schauder fixed point theorem

2015-12-07

四川省教育厅自然科学青年基金(12ZB108)

李海艳(1983—),女,讲师,主要从事非线性泛函分析的研究,E-mail:jclihaiyan2012@163.com

O175.8

A

1001-8395(2017)02-0163-09

10.3969/j.issn.1001-8395.2017.02.004