剑指圆锥曲线最值问题

■浙江省桐庐富春高级中学 张玉红

剑指圆锥曲线最值问题

■浙江省桐庐富春高级中学 张玉红

圆锥曲线最值问题,历来是高考常考题型。此类问题涉及知识面较广,解法灵活多变,但总体上主要有两种方法：一是利用几何法,即通过曲线的定义、几何性质以及平面几何中的定理、性质等进行求解;二是利用代数法,即把要求最值的几何量或代数表达式表示为某个(些)参数的函数解析式,然后利用函数方法、不等式方法再进行求解。下面举例说明。

一、利用定义，直奔主题

例1 已知双曲线C的两个焦点分别为F1(-2,0),F2(2,0),双曲线C上一点P到F1,F2的距离差的绝对值等于2。

(1)求双曲线C的标准方程;

(2)已知定点G(1,2),点D是双曲线C右支上的动点,求|D F1|+|D G|的最小值。

解析：(1)依题意,得双曲线C的半实轴长为a=1,半焦距为c=2。

(2)由已知得|D F1|-|D F2|=2,即|D F1|=|D F2|+2。

所以|D F1|+|D G|=|D F2|+|D G|+ 2≥|G F2|+2,当且仅当G、D、F2三点共线时取等号。

因为|G F2|=,所以|D F2|+|D G|+2≥|G F2|+2=5+2。

故|D F1|+|D G|的最小值为5+2。

点评：利用双曲线的定义,可以将圆锥曲线的最值问题转化为几何问题来处理。

二、函数思想，为你着想

图1

解析：(1)y2=2p x(p＞0)的准线为x=

故抛物线C的方程为y2=x。

又点M(t,1)在曲线C上,所以t=1。

(2)由(1)知,点M坐标为(1,1),从而n =m,即点Q(m,m)。

依题意知直线A B的斜率存在,且不为0。

设直线A B的斜率为k(k≠0),且A(x1,y1),B(x2,y2)。

所以Δ=4m-4m2＞0,y1+y2=2m, y1y2=2m2-m。

点评：函数法是探求解析几何最值问题的首选方法,主要涉及二次函数、无理函数等,可利用函数的单调性或基本不等式求出它的最值。

三、数形结合，立竿见影

解析：如图2,设过Q(4,3)的直线方程为y =k(x-4)+3,即k=

图2

点评：利用数形结合,挖掘数学表达式的几何特征,并画出图形,从图形中发现与圆锥曲线最值有关的信息,这类最值问题一般与曲线的切线有关。

四、三角换元，最值速现

(1)求x2+y2的最值;

(2)若四边形A B C D内接于椭圆E,点A的横坐标为5,点C的纵坐标为4,求四边形A B C D面积的最大值。

(2)如图3所示,易知A(5,0),C(0,4)。

设B(5 c o sθ,4 s i nθ)为椭圆上任一点,

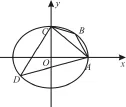
图3

所以点B到直线A C的距离为：

同理可得,点D到直线A C的距离d2满足：

点评：三角换元的目的是把目标函数中两个变量转化为一个角变量,从而把原问题转化为我们熟知的三角函数最值问题。

(责任编辑 徐利杰)