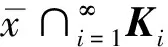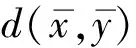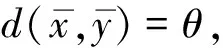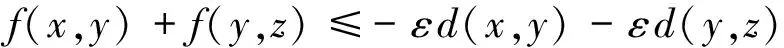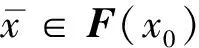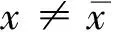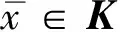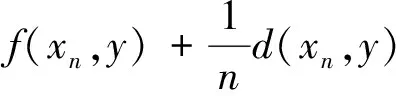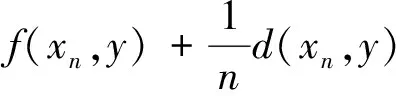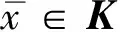锥b－度量空间中向量平衡问题解的存在性

吴贤璇，鲁晓峰

( 广东工业大学 应用数学学院，广东 广州 510520)

锥b－度量空间中向量平衡问题解的存在性

吴贤璇，鲁晓峰

( 广东工业大学 应用数学学院，广东 广州 510520)

研究了锥b-度量空间中向量平衡问题解的存在性问题.利用向量空间中的序方法证明了向量形式的Ekeland变分原理,并给出了锥b-度量空间上向量平衡问题解的存在性定理.结果表明,如果向量值函数上半连续且满足向量形式的Ekeland变分原理的条件,那么向量平衡问题的解集非空。

锥b-度量空间;Ekeland变分原理;向量平衡问题

0 引言

向量平衡问题备受国内外学者的关注.基于非线性分析中广泛使用的Ekeland变分原理[2],Bianchi等[2]构造实值函数将向量映射为非负数,指出向量平衡问题解集非空;Ansari[3]利用非线性标量函数解决了拟度量空间上的向量均衡问题;成波等[4]证明了度量空间上向量均衡系统的解的存在性;王月虎等[5]在考虑向量平衡问题的解时,巧妙地将Bianchi等[2]的方法应用在锥度量空间上.

至今,向量平衡问题的解决需要构造非线性标量函数,将向量问题转化为数量问题.本文将文献[5]中的锥度量空间和n维欧式空间分别推广为锥b-度量空间[6]和赋范空间,利用向量空间中的序方法证明了向量形式的Ekeland变分原理[3],给出了锥b-度量空间[6]上向量平衡问题解的存在性结果.

1 预备知识

为了叙述方便，先引入本文所要用到的基本定义和已知结果.

定义1[7]设Y是一个赋范线性空间，θ是Y中的零元素,如果C是Y中的一个非空闭凸集,并且满足下列两个条件：

1)x∈C,λ≥⟹λx∈C;

2)x∈C,-x∈C⟹x=θ;

则称C是Y中的一个锥.

定义2[7]在中给定一个锥C后，则可在Y中的元素间引入偏序：

y1≤y2⟺y2-y1∈C, ∀y1,y2∈Y

y1≤y2⟺y2-y1∈intC, ∀y1,y2∈Y

定义3[7]设C⊂Y,Z⊂Y,若对∀x∈C,均有z≤x;同时,从z1≤x,(∀x∈C),可推出z1≤z;则称z是C的下确界，记为infC;若Y中任何有下界的锥C都具有下确界，则称锥C是强极小锥.

定义4[6]令X是一个非空集合，Y是一个赋范空间，若d∶X×X→Y，满足下列条件：

1)d(x,y)>θ,∀x,y∈X,x≠y；d(x,y)=θ当且仅当x=y；

2)d(x,y)=d(y,x),∀x,y∈X；

3)d(x,y)≤sd(x,z)+sd(z,y),∀x,y,z∈X,(s≥1).

那么d称为X上的一个带有系数s的锥b-度量,同时称(X,d)为锥b-度量空间.

注：很明显，若条件3)中s=1，则不等式d(x,y)≤d(x,z)+sd(z,y)在锥度量空间中是满足的；当s>1时，该不等式在锥度量空间中是不对的.因此，锥b-度量空间有效的推广了锥度量空间，每一个锥度量空间是锥b-度量空间，反过来则错误。

定义5[6](X,d)是一个锥b-度量空间,令{xn}是(X,d)中的序列,x∈(X,d) ,则可以说{xn}是:

1)柯西序列，如果对∀c∈Y且θ<0,对∀n,m>N,有d(xn,xm)<

2)收敛序列，如果对∀c∈Y且θ<0,对∀n>N,有d(xn,x)<

这种情况下,xn的极限是x，即xn→x,(n→∞) .

定义6[6](X,d)是一个锥b-度量空间,

1)如果每个柯西序列都收敛，则(X,d)是完备的;

2)如果每个收敛列{xn}在(X,d)中有收敛子列，则(X,d)是序列紧致的.

定义7[5](X,d)令是完备的锥b-度量空间,Y是一个赋范线性空间,C是Y中的锥.

向量值函数f∶(X,d)→Y.

1)在x0∈(X,d)是拟下半连续,则对∀x0c∈(X,d),b∈Y,有b/≥f(x0),存在x0的一个邻域U,使得b/≥f(x),∀x∈U.若f在(X,d)上每一个点都拟下半连续，则f在(X,d)上拟下半连续.

2) 在x0∈(X,d)是上半连续,则对x0∈(X,d),f(x0)的任意一个邻域V,存在x0的一个邻域U,使得f(U)⊂f(x0)+V-C.

定义8[5]令(X,d)是一个锥度量空间,K是(X,d)中的非空子集，则K的距离可以定义为：

引理1[8]令(X,d)是一个完备的锥b-度量空间,Y是一个赋范空间,C是Y中的锥 .f∶(X,d)→Y在(X,d)中是拟下半连续,当且仅当L(f,b)={x∈X,f(x)≤b}在X中是闭的,∀b∈Y.

2 主要结果

所以对∀ε>0,∃N>0,当i>N时,

diam(Ki)<ε

由于Ki非空,可取xi∈Ki,i∈N+,对序列{xi}i∈N+有

即 ‖d(xi,yi)‖→0(i,j→∞)

所以d(xi,yi)→θ(i,j→∞)

因此{xi}i∈N+为柯西列.

定理2 令(X，d)是完备的锥b-度量空间,Y是一个赋范空间,C是Y中的一个强极小锥,f∶X×X→Y,假设下列条件满足：

1)f(u,u)=θ,∀u∈(X,d);

2)f(x,·)有下界，∀x∈(X,d);

3)f(z,y)+f(y,x)∈f(z,x)+C,∀x,y,z∈(X,d);

4)f(x,·)是拟下半连续，∀x∈(X,d);f(·,y)是上半连续，∀y∈(X,d).

证明 令F(x)={y∈(X,d)∶f(x,y)+εd(x,y)∈-C},∀x∈(X,d),由条件1),4)和引理1,可知对∀x∈(X,d),F(x)是一个非空且闭的集合.

假设y∈F(x),则f(x,y)+εd(x,y)∈-C,所以

(1)

假设,z∈F(y),则f(y,z)+εd(y,z)∈-C,所以

(2)

因为(X,d)是锥b-度量空间，所以对任意x,y,z∈(X,d),有

(3)

(4)

由(1)(2)可得

(5)

由(3)(4)(5)可得

所以f(x,z)+εd(x,z)≤θ

即f(x,z)+εd(x,z)∈-C,z∈F(x)

所以F(y)⊂F(x) .

所以f(x,z)≥v(x)

即 -f(x,z)≤v(x)

若z∈F(x),则存在一个κ∈C,使得

f(x,z)+εd(x,z)=-κ

所以 -f(x,z)-εd(x,z)=κ∈C

则εd(x,z) ≤f(x,z)≤-v(x)

(6)

对∀x1,x2∈F(x),有

(7)

由(6)(7)可得，

从x0开始，构建一个序列xn,满足xn+1∈F(xn),且有e∈C,使得

(8)

由条件3)可得f(z,x)≤f(z,y)+f(y,x) ,

(9)

由(9)及v(x)的定义可得:

(10)

由(8)(10)可得

当n→∞时,d(x1,x2)≤θ(n→∞) .

因为d(x1,x2)≥θ,所以当n→∞时,d(x1,x2)→θ. 由x1,x2的任意性,可知

注1 定理2的结论b)蕴含着

注2 若用X的非空闭子集K代替X,定理2的结论依然成立.

定理3 令(X,d)是完备的锥b-度量空间,Y是一个赋范空间,C是Y中的一个强极小锥,K是X中的非空紧集,f∶K×K→Y,假设下列条件满足：

1)f(u,u)=θ,∀u∈K;

2)f(x,·)有下界，∀x∈K;

3)sf(z,y)+sf(y,x)∈f(z,x)+C,∀x,y,z∈(X,d),s≥1;

4)f(x,·)是拟下半连续，对∀x∈K;f(·,y)是上半连续，∀y∈K；

由定理2注1可知,对任意n∈N,∃xn∈K,有

(11)

相反地,假设存在y*∈K,使得

f(xnk,y*)∈-intC

所以当nk足够大时,有

而这与(11)矛盾,因此,

推论 若定理2中(X,d)为序列紧的完备锥b-度量空间,显然向量平衡问题的解集非空.

[1]Marco Castellani,Massimo Pappalardo,Mauro Passacantando. Existence results for nonconvex equilibrium problems [J]. Optimization Methods and Software,2010,(3):312～315.

[2]Bianchi M, Kassay G, Pini R. Ekeland’s principle for vector equilibrium problems [J]. Nonlinear Analysis, 2007, 66(7): 1454～1464.

[3]Ansari Q H.Vectorial form of Ekeland-type variational princeple with applications to vector equilibrium problems and fixed point theory[J]. Journal of Mathematical Analysis and Applications, 2007, 334: 561～575.

[4]成 波,刘三阳. Ekeland变分原理导出的向量均衡系统解的存在性[J]. 工程数学学报,2010,(3):562～566.

[5]王月虎,张从军. 锥度量空间中基于Ekeland变分原理的向量均衡问题的解的存在性(英)[J]. 数学杂志,2015,(4):825～832.

[6]Hussain N, Shah M H. KKM mappings in cone b-metric spaces [J]. Computers & Mathematics with Applications,2011,62:626～628.

[7]郭大钧. 非线性泛函分析[M]. 济南:山东科学技术出版社,1984.

[8]Qiu Jing-Hui. An equilibrium version of vectorial Ekeland variational principle and its applications to equilibrium problems [J], Nonlinear Analysis: Real World Applications, 2016, 27: 26～42.

Existence of solutions for vector equilibrium problems in coneb-metric spaces

WU Xian-xuan, LU Xiao-feng

(Guangdong University of Technology, School of Applied Mathematics, Guangzhou, Guangdong 510520)

This paper studies the existence of solutions for vector equilibrium problems in coneb-metric spaces. By using the vector ordering method, we prove a vector form of Ekeland’s variational principle and give the existence theorem of vector equilibrium problems in coneb-metric spaces. Our results show that, if the vector-valued function is upper semi-continuous and satisfies assumptions of the vector form Ekeland’s variational principle, then the set of solutions for the vector equilibrium problem is nonempty.

coneb-metric space; Ekeland’s variational principle; vector equilibrium problem

2016—08—23

国家自然科学基金(10871052),非线性分析中的一些问题.

吴贤璇(1991— ),女,汉族,广东省汕头市人,硕士研究生,研究方向非线性泛函分析.

O151

A

2096-3149(2017)01- 0056-05

10.3969/j.issn.2096-3149.2017.01.012