一道“解析几何”模拟考题的解法探究

北京市第八十中学 (100102) 孙世林

一道“解析几何”模拟考题的解法探究

北京市第八十中学 (100102) 孙世林

解析几何的综合问题，已知条件多，题干长，常涉及多个知识点，对能力要求高，不少同学感到思路不清，难以入手，鉴于此，笔者结合今年北京市高考模拟解析几何试题，谈谈个人的一些想法，谈谈如何自然形成解题思路，供大家参考．

一、从已知出发，循序渐进自然生成

已知条件是我们解题的重要依据，解题时要认真阅读已知，准确把握已知给了我们那些信息？这些信息之间有什么关系？全面分析这些已知条件还可以得出那些结论？这些结论和我们所要求的结论有什么关系？另外，还有要充分挖掘题目中隐藏的已知条件有哪些？弄清了这些问题，解题思路便可自然生成，问题不攻自破．

例1 (2017年高考西城区第一次模拟考试，理科19题)

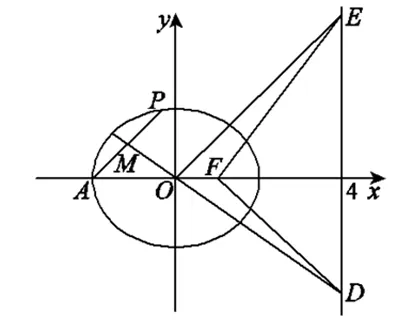
图1

(1)求椭圆C的方程；

(2)设O为原点，P为椭圆上一点，AP的中点为M．直线OM与直线x=4交于点D，过O且平行于AP的直线与直线x=4交于点E．求证：∠ODF=∠OEF．

分析1：本题的第一问很容易解决，第二问中P为椭圆上一点，AP的中点M与原点O连接并延长与直线x=4相交，形成了点D，点E是过O且平行于AP的直线与直线x=4相交形成的，这样才出现了线段DF和EF，可见DF和EF都与点P有紧密的联系，所以我们就应从点P入手探究点D与点E具有怎样的位置关系？研究发现点D与点E与x轴没有对称关系，这样自然引领我们来要探究EF与P点有紧密联系的直线MD的位置关系，接下来再探究FD与OE的位置关系，这样本题的解题思路就生成了.

(2)由(1)得A(-2,0)．设AP的中点M(x0,y0)，P(x1,y1)．

图2

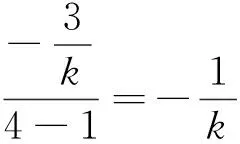
评析：通过上述分析及解题过程可以看出解题思路的形成是从已知入手，从已知条件间的联系出发，探究从已知得出的相关点、线、角间的关系，循序渐进地得出所要求的结论．因此解题中要善于利用已知条件，这里所说的已知条件既有题目中直接给出的，也有隐含的需要我们进一步挖掘才能得出的条件．

分析2：如何使解题过程简便快捷，运算量小一些，一直是考生们所追求的，在解法一中，我们从直线AP的方程出发，运算量略显大些，如何解决？在本题中，点P为椭圆上的动点，点E和点D随着点P的运动变化而变化，所以点P的运动变化是主动的，所以我们从点P的坐标出发，用点P的坐标表示点E和点D的坐标，从而刻画EF和FD的运动变化，探究EF与直线MD的位置关系，这样，从点P的坐标入手成为了解决本题的自然选择．

评析：解析几何综合问题常在运动变化过程中探究某些不变的性质与规律，对于这类运动变化问题，解题时要从已知出发深入探究产生运动变化的根源，从产生运动变化的根源入手，选择好从直线方程入手还是从点的坐标入手，就可以简化计算过程，自然快捷地解决此类问题．

二、从结论入手，执果索因由此及彼

例2 (2017年高考北京市海淀区第一次模拟考试，文科19题)

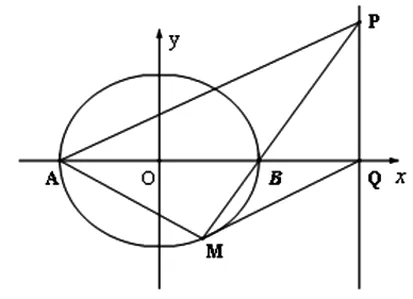
图3

(1)求椭圆C的方程；

(2)设点Q(4,0), 若点P在直线x=4上，直线BP与椭圆交于另一点M.判断是否存在点P，使得四边形APQM为梯形？若存在，求出点P的坐标；若不存在，说明理由.

分析：是否存在点P，使得四边形APQM为梯形？很自然想到假设成立，将四边形APQM为梯形视为已知反推点P所满足的条件，由已知显然AM,PQ不平行，所以AP与MQ平行，由平行我们又很自然地想到斜率相等，在AP与MQ斜率相等的条件求得点P的坐标，这里我们可以有三种思路.

思路一：因为点P在直线x=4上，所以可设点P(4,y0)，由此得出直线BP的方程，从而用点P的坐标P(4,y0)表示点M的坐标，最后利用AP与MQ斜率相等的条件求得点P的坐标．

思路二：从直线AP入手，由于点A已知，所以设AP所在直线为y=k(x+2)，利用点P在直线x=4上将点P的坐标用k表示，从而得出直线BP的方程，利用点M是直线BP与椭圆的交点，将点M坐标也用k表示，最后利用AP与MQ斜率相等的条件求点P的坐标；本思路中要经历两次解方程组，特别是求点M坐标时要注意韦达定理的应用，以简化运算．

思路三：从直线BP入手，由于点B已知，所以设BP所在直线为x=ty+2，利用点P在直线x=4上将点P的坐标用t表示，利用点M是BP与椭圆的交点，将点M坐标也用t表示，最后利用AP与MQ斜率相等的条件求点P的坐标；观察发现直线BP一定存在斜率，所以本思路中直线BP的方程我们采取了横截距式，与思路二对比大大降低了运算量．

(2)假设存在点P,使得四边形APQM为梯形.

由题可知，显然AM,PQ不平行，所以AP与MQ平行，即kAP=kMQ.

(2)假设存在点P,使得四边形APQM为梯形.

由题可知，显然AM,PQ不平行，所以AP与MQ平行,kAP=kMQ，显然直线AP斜率存在，设直线AP方程为y=k(x+2).

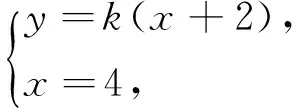
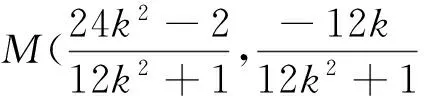
(2)假设存在点P,使得四边形APQM为梯形.

由题可知，显然AM,PQ不平行，所以AP与MQ平行,kAP=kMQ.

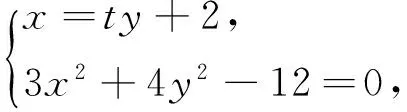
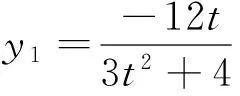
评析：在解决解析几何综合问题时，有时若从直接求解，常常感觉不知从何入手，我们可以尝试从结论入手，观察结论和已知条件有什么关系？探究结论成立时应满足什么条件？执果索因，往往可使解题思路豁然开朗．

三、善于将问题进行转化，从几何角度寻求突破

“解析几何”首先是几何问题，利用平面几何知识解决问题也是不可或缺的方法，解析几何问题中蕴含很多几何条件，这些几何条件间有什么关系？从某些几何条件出发能得到什么样的新几何关系？某些几何关系成立需要有怎样的几何条件？随着这些疑问的探究和解决，解题思路也就自然的生成了，请看例2的第四种解题思路：

图4

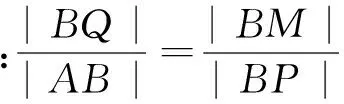
从而得出点P的坐标．

评析：解析几何的核心方法是用代数的方法研究几何问题，在解题过程中，利用平面几何知识研究题目中的几何关系是必要的，在这个过程中要经历文字信息、图形特征和符号语言之间的多重转换，因此，我们必须重视对几何关系的深入研究，使用恰当的代数形式表示题目中的几何关系，从而形成正确的解题思路．

解析几何综合题综合性强，能力要求高，是每年高考的热点，也是重点；高考的解析几何考题常考常新，难免会遇到陌生的题目，但陌生往往只是在形式上，本质不会超出我们所学的知识范畴，只要我们遵循解题的基本规律，抓住学科知识本质，认真探究已知、结论间的本质联系，解题思路定会“柳暗花明”，事半功倍地解决好解析几何的综合问题．

[1]朱玉群.对解题思路自然生成的几点感悟[J]，中学数学(上),2016(12)80-82；

[2]孙世林.探究几何关系代数化的有效策略[J]，高中数理化(上)，2015(11)1-2.