利用函数思想巧解等差数列问题

张志鹏

数列是特殊的函数，而等差数列更是具备良好的函数性质，要是我们能够利用好这些性质，不仅能够使我们加深对数列的理解，更能使我们解决相应问题时更加得心应手.

一、等差数列中特定项的问题

我们假设数列{an}为等差数列，其公差为d，首项为a1.则易知其通项公式为an=a1+（n-1）dan=nd+（a1-d），若将an看成n的函数，我们会发现an是形如“kn+b”的关于n的线性函数，其中k等于公差d.既然是线性函数，我们知道其上任意的点都是“共线”的，利用这条性质我们便可以方便、高效地解决相应的类型问题.

例1已知数列{an}为等差数列，且a3=7，a15=31，则a17的值为.

常规解法由于{an}为等差数列，所以有a15=a1+14d；a3=a1+2d.求得首项a1=3，公差d=2，故a17=a1+16d=35.

巧妙解法由于{an}为等差数列，则易知（3，a3），（15，a15），（17，a17）三點共线，故其“斜率”相等，因而，我们得a15-a3115-3=a17-a15117-15，代入相应的值后我们解得a17=35.

点评：对于常规思路，要解决等差数列通项类的问题，我们一般需要转换为首项a1和公差d来进行求解，需要两个方程来解出这两个参数，而我们从函数视角来解决此类问题时巧妙利用通项公式的函数特征，只需一步便可求得答案，无疑降低了计算量.

二、等差数列中前n项和的问题

设数列{an}为等差数列，其公差为d，首项为a1，则其前n项和sn=n（a1+an）12=d12n2+a1-d12n.若我们将sn看成n的函数，当公差d≠0时我们会发现sn是形如“an2+bn”的关于n的二次函数，并且其函数图像过定点（0，0）.于是我们在解题时若能通过对二次函数图像的解读，并利用数形结合的思想来考虑问题，我们便可以快速找到相应的突破口.而函数g（n）=sn1n则是关于n的一次函数，既然是线性函数，我们知道其上任意的点都是“共线”的，利用这条性质我们也可以方便、高效地解决相应的类型问题.

例2已知等差数列{an}的前m项和为30，前2m项的和为100，求数列前5m项的和s5m的值.

常规解法由于{an}为等差数列，所以sm，s2m-sm，s3m-s2m，s4m-s3m，s5m-s4m仍为等差数列，故由题目可知sm，s2m-sm，s3m-s2m，s4m-s3m，s5m-s4m的值依次为30，70，110，150，190，所以s5m=30+70+110+150+190=550.

巧妙解法构造函数g（n）=sn1n，易知g（n）是关于n的一次函数.既然是线性函数，我们知道其上任意的点都是“共线”的，所以我们有：m，sm1m，2m，s2m12m，5m，s5m15m三点共线，因而，有s2m12m-sm1m12m-m=s5m15m-s2m12m15m-2m，代入解得s5m=550.

点评：常规解法利用了等差数列依次k项和仍为等差数列这一重要性质，但是当求和项太多时，例如，此题中求s100m，这类办法便显得不那么高明了，而我们创造性地构造g（n）=sn1n这一函数，利用其线性特征，便可以直接求出所需的前5m项之和，且此类方法不受求和项数量影响.

例3首项为正数的等差数列，前n项和为sn，并且s3=s8则当sn取得最大值时，n的值为.

常规解法由题可知公差d<0并有3a2=4（a4+a5），所以a2=-4d，故an=（n-6）d，所以a6=0.因此，前5项或者前6项的和最大，因此，答案为5或6.

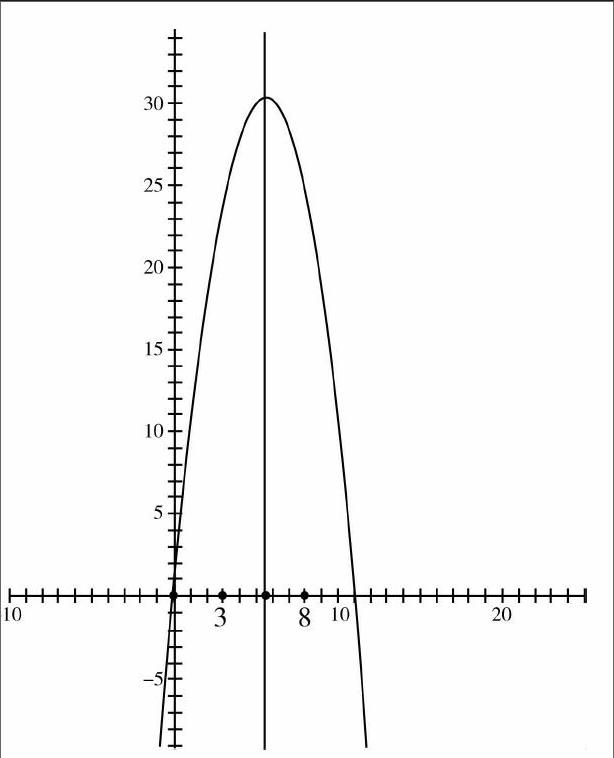
巧妙解法由题可知s1=a1>0，并且公差d<0，因此，数列sn=d12n2+a1-d12n所对应的点所在函数的图像如下图所示.

由于s3=s8，所以对称轴为n=3+812=5.5，又因为n为正整数且|5-5.5|=|6-5.5|，所以，前5项或者前6项的和相等，此时均取得最大值，因此，答案填5或6.

点评：题目直接告诉了我们sn中特定两项的关系，而常规解法是将sn转化为an来进行求解的，这不免走了一些弯路，而从函数视角出发，直接利用题目所给已知条件，抓住二次函数这一我们非常熟悉的函数的特征来解决问题，直奔主题，简洁明了.