关于高中几何概型问题的几点注记
李 伟
(辽宁省鞍山市第三中学,辽宁 鞍山 114000)
关于高中几何概型问题的几点注记
李 伟
(辽宁省鞍山市第三中学,辽宁 鞍山 114000)
由于几何概型既不同于古典概型、也不是公理化的概率定义,所以人们在认识上存在很多差异,进而导致出现各种问题.本文试图揭示几何概型悖论出现的原因;抽象代数意义同构背景下的等可能转换;维度对解决几何概型问题的影响,最后介绍从临界条件、线性规划入手分析解决几何概型的解题方法.
几何概型悖论;概率公理化定义;同构的概念;临界条件
几何概型不论在高中数学教学,还是在高考数学科命题中都占有一定的地位,但限于高中阶段其理论不完备,所以在教学中时常出现一些令人费解的问题困扰师生.本文的目的是就高中数学中的几何概型谈一些认识,试图使那些费解的问题成为显然.
一、关于几何概型悖论的存在性问题
法国学者贝特朗围绕几何概型提出了著名的悖论问题,后人称其为贝特朗几何概型悖论,对此[文献1]中已作出详尽的说明,本文不在陈述.下面要探讨的问题是关于几何概型悖论存在的原因及分析.
关于概率论的最早专著是十八世纪瑞士数学家雅克布.伯努利所写的《猜测术》(见[文献2]),随着二十世纪概率公理化定义的出现,逐步形成比较完整的数学分支.概率论发展历程是从不严密的日常生活现象分析走向具有严谨数学体系的过程,而古典概型、几何概型恰巧是在概率论理论体系不完善时出现的(即使现行教材中给出的相关概念也是描述性的,缺乏公理建构意义下的准确性).那么,概率的公理化定义对认识几何概型悖论有何指导意义?我们从分析概率论的公理化定义(见[文献3])入手进行探究.
概率公理化定义:设E是随机试验,Ω是它的样本空间,若对于E的每一个事件A都赋予一个实数P(A),它满足以下三个条件:(1)对于每一事件A有0≤P(A)≤1 , (2)P(Ω)=1,(3)可列可加性:设A1,A2,…是两两互不相容的事件,则P(A1∪A2∪…)=P(A1)+P(A2)+…则称P(A)为事件A发生的概率.
从该定义来看,解决概率问题的前提一是要明确随机试验是什么?二是要明确样本空间的结构是什么?然
后才能开始着手分析解决相关问题.下面通过例子来分析几何概型悖论产生原因.

例1 如图所示,在等腰直角△ABC中,过直角顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,求AM 解析1 在AB上取AD=AC,连接CD,有∠ACD=∠ADC,故欲使∠AM 原因分析 前者是把角区域作为样本空间求解;后者是把线段区域作为样本空间求解,哪个思考是正确的? 准确理解题意,明确试验对象,正确选择自变量是求解几何概型问题的关键.本题中的试验对象是“射线CM”,其位置可用∠ACM(自变量)的大小来度量.因此本题是关于角的概率问题.题目中所有角构成的样本空间Ω是∠ACB=90°;符合题目要求的角(∠ACM)构成的事件A是∠ACM<67.5°.因此解析1是正确的. 而解题2找错了试验对象,误把线段AM作为试验对象,与原题给出的条件不符.特别是线段AM的长与∠ACM的大小不成正比例,因此导致计算结果错误. 因此,从上例看出,几何概型悖论产生的原因是解题时,没有搞清楚随机试验是什么?样本空间的结构是什么?而靠主管臆断出现了解题失误.所以,对于中学数学教学中遇到的概念问题,有时确实需要我们要站在高等数学的角度来审视、重新认识,并给出具有前瞻性的解释. 继续剖析上述问题,事实上我们也遇到过这样的几何概型问题(不讨论其解法是否正确,只看结果是否一致),从角区域、线段区域两方面作为样本空间来解决其答案是一样的.这是什么原因哪?原因是样本空间的等可能转换问题.也就是说,不同的样本空间,如果他们之间存在等可能转化,在此前提下其概率结果也是一致的.请看下面的例子: 例2 已知半径为1,圆心角为直角的扇形OAB,引射线OM交弧AB于点M,求弧AM 分析 引入弧度制的主要原因是在单位圆内实现了角的度量和线段度量的统一.在弧度制度量角的前提下,本题分别采取角区域和弧长作为样本空间去思考,所求概率值是一致的.原因就是弧长=对应圆心角的弧度数,这个等式保证了角与弧长大小的等可能转化,因此结果是一致的. 对于前述例1而言,线段区域与角区域之间通过随机试验做射线,确实实现了抽象代数意义下的同构(两个集合之间存在一一对应),依据同构理论,它们应该具有相同的代数性质.但我们应该注意到的是它们两者是不能够实现等可能转化.事实上增加(或减少)等量的角,对应的线段 变化的长度是不同的(不成比例),反之亦然.这也是两种算法结论不同的原因. 解决几何概型的问题只要把线段、平面、空间的样本区域、事件区域划分搞清楚,求解就是显然的了.通过教学实践发现用临界条件寻求区域的划分是解决几何概型的好办法.见下面的例子. 解析 本题的样本空间区域是显然的.关键是确定事件空间区域,即求使得∠AOC和∠BOC都不小于π/6的区域.由题意知临界角为π/6,所以(如上图)首先作出∠BOM=∠AON=π/6,此时略加分析知,只需点C落在弧MN内即可. 另,从弧长与角度的等可能转换来看,本题从弧长角度求解答案也是一致的(当然解法是不科学的). [文献4]中提出一个问题:“在一条线段上任取一点,则取到中点的概率是多少?”笔者认为,此题在陈述上有所缺欠.大家知道,高中几何概型中涉及的维度是一、二、三维(即直线、平面、空间),即使几何概型基本思考元素是“点”,或者说点是构成线、面、体的最基本要素,但在解决实际问题时,样本空间也好、事件也好都是在同一维度内以线段、平面图形、几何体的形式出现,跨维度(样本空间与事件空间不是一个维度)是没有意义的. [文献4]中提出的问题,之所以在陈述上值得商榷就在于“点”是0维、线段是一维.0维的点做事件,一维的线段做样本空间,不仅在逻辑上是说不过去的,仅就在计算上它们就不是可通约量(单位不一致).所以要求不能跨维度去讨论样本和事件.类似的在平面图形中讨论线段,在空间体中讨论平面图形的概率一样是没有意义的. 请看下面的例子. 例4 已知某公交车每10min一班,在车站停1min.则乘客到达站台立即乘上车的概率为____. 类似的,在平面图形中讨论线段的概率和几何体中讨论平面图形的概率,一样是没有意义的.为了更明晰,请见下面的例子. 例5 在长为10 cm的线段AB上任取一点P,并以线段AP为边作正方形,这个正方形的面积介于25 cm2与49 cm2之间的概率为( ). 解析 题中尽管提到点P,事实上我们解题时是用面积表示样本和样本空间,道理同上.求解很显然,在此略去. 上面已经介绍了用临界条件确定事件区域的解题方法可提高解决几何概型的解题速度,下面针对二维的多边形事件问题介绍一种解决办法,即用求解简单线性规划的方法确定事件区域.请看下面的例子. 小结:本题也是“会面”问题,只是提法有所差异.线 性规划的解题思想同样得到应用. 到此,本文介绍了解决几何概型的注意事项、思考方法,同时对解决几何概型易出现的问题提供了一些思考,就处理几何概型的一些方法和手段也同时作了说明,目的是澄清一些错误认识,改进解题方法、提高解题效率. [1]郑甜.几何概型中类似“贝特朗概率悖论”的一点思考[J].新课程,2015(02). [2]霍华德.伊夫斯【美】.数学史概论(第六版)[M]. 哈尔滨:哈尔滨工业大学出版社,2009. [3]孙振绮.概率论与数理统计(第二版)[M].北京:机械工业出版社,2012(02). [4]胡浩.由一道几何概型题引发的思考[J].中国数学教育(高中版),2017(03),61-62. [责任编辑:杨惠民] 2017-05-01 李伟,男,辽宁省鞍山市第三中学党委书记、数学特级教师,辽宁省高中数学科专家组成员,辽宁省教育学会理事,中国数学奥利匹克一级教练员. G632 B 1008-0333(2017)16-0002-03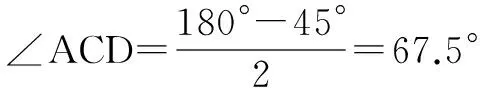

二、关于解决几何概型问题中的等可能转换问题

三、关于用临界条件解决几何概型问题

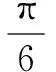
四、关于解决几何概型问题中维度问题
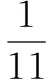
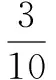
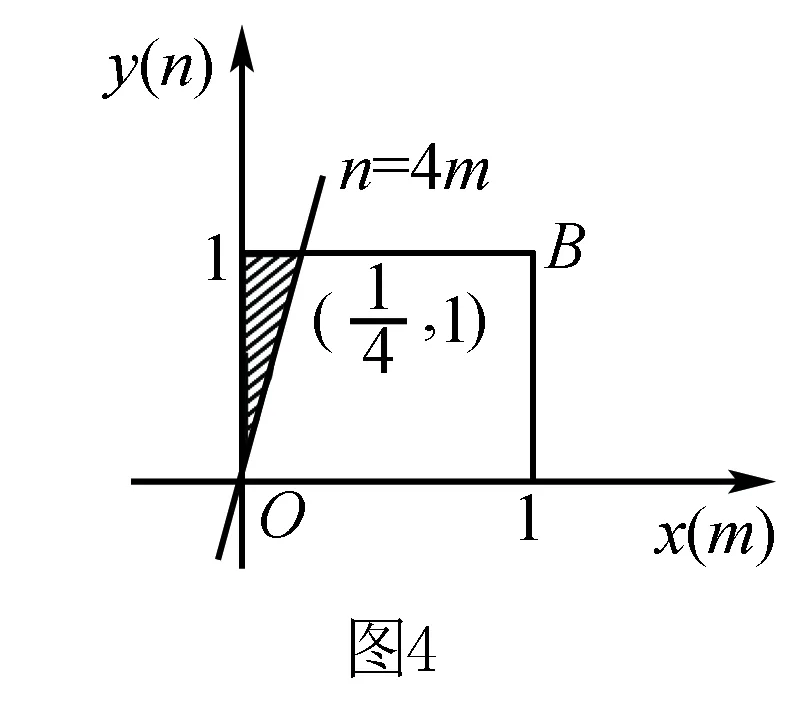
五、用简单线性规划解决二维几何概型问题