例谈求参问题的解题策略

岳茂富

(山东省宁阳县第二实验中学,山东 泰安 271400)



例谈求参问题的解题策略

岳茂富

(山东省宁阳县第二实验中学,山东 泰安 271400)

函数中的求参问题是高中阶段一种重要题型，本文提供了四种求参方法，旨在培养学生通过对题目信息的分析以期在第一时间内选择恰当的解题方法的能力.

求参;分离;讨论;特值;放缩;能力;反思;数学思维

波利亚说：“中学数学教学的首要任务就是加强解题训练.”而解题方法的优劣关乎解题效率.对于同一类型的题目，因方法选择的不同，会使解题过程的繁简程度大不一样，思维量也有很大的不同.求参数的取值范围一直以来为高考命题者所钟爱，此种题目的解题方法也逐渐由单一走向多姿多彩.笔者结合近几年求参数范围题目的变化归纳了以下几种方法，方便大家在做此类题目时根据题目特点进行恰当选择.

一、分离参数法

分离参数法是最基本也是最常用的求参数范围的方法，大体分两步，一是分离，二是求函数值域.

例1 (2013年新课标Ⅰ卷理21)已知函数f(x)=x2+ax+b，g(x)=ex(cx+d)，若曲线y=f(x)和曲线y=g(x)都过点P(0,2)，且在点P处有相同的切线y=4x+2.

(Ⅰ)求a，b，c，d的值;

(Ⅱ)若x≥-2时，f(x)≤kg(x)，求k的取值范围.

解析 (Ⅰ)由已知得f(0)=2，g(0)=2，f′(0)=4，g′(0)=4.

而f′(x)=2x+b，g′(x)=ex(cx+d+c)，∴a=4，b=2，c=2，d=2.

(Ⅱ)当x≥-2时，x2+4x+2≤2kex(x+1)

①当x=-1时，-1≤0恒成立，所以k∈R.

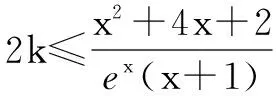
综上所述，k的取值范围是[1,e2].

二、讨论求参

自导数进入高中教材以来，在解答题中求参数取值范围的方法不再单调，其中计算函数导数后分类讨论求参数的范围在每年高考题目中都有所涉及.这种题目若采用分离参数法，在求函数值域的时候会遇到瓶颈，这时往往要求导后通过讨论参数的范围判断函数的单调性，借助函数的零点寻找满足题意的参数范围.

例2 (2014新课标Ⅱ卷理21)已知函数f(x)=ex-e-x-2x.

(Ⅰ)讨论f(x)的单调性；(Ⅱ)设g(x)=f(2x)-4bf(x)，当x>0时，g(x)>0,求b的最大值；(Ⅲ)略.

解析 (Ⅰ)略；

(Ⅱ)g(x)=f(2x)-4bf(x)=e2x-e-2x-4x-4b(ex-e-x-2x)，显然g(0)=0，g′(x)=2(e2x+e-2x-2)-4b(ex+e-x-2)=2(ex-e-x)2-4b(ex/2-e-x/2)2=2(ex/2+e-x/2)2(ex/2-e-x/2)2-4b(ex/2-e-x/2)2=2(ex/2-e-x/2)2[(ex/2+e-x/2)2-2b]，

因为x>0，所以ex/2+e-x/2>2，(ex/2+e-x/2)2>4，

当2b≤4，即b≤2时，g′(x)>0，所以g(x)在(0,+∞)上为增函数，所以g(x)>g(0)=0，所以b≤2满足题意.

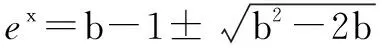
综上知，b≤2.

三、特值辅助求参

对于在某个区间内的不等式恒成立求参问题，可以根据题目特点，选取适当的特值代入不等式求得参数的一个范围，而参数的准确范围显然是由这个特值求得的范围的子集，但是这个范围对于进一步求参数的准确范围有时会起到事半功备的效果.

例3 (2012浙江名校联考)已知函数f(x)=ex(ax2+a+1)(a∈R).

(Ⅰ)若a=-1，求曲线y=f(x)在点(1,f(1))处的切线方程；

四、放缩求参

若f(x)≥g(x)，求f(x)≥h(x)恒成的某参数的取值范围，若参数的准确范围满足g(x)≥h(x)(这是出题背景)，这时可以通过g(x)≥h(x)求参数的范围.此种方法在2013年辽宁高考题中出现，题目中第二问的解决紧紧依赖第一问所证明的结论铺垫.

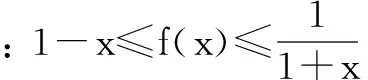
(Ⅱ)若f(x)≥g(x)恒成立，求实数a的取值范围.

解析 (Ⅰ)略.

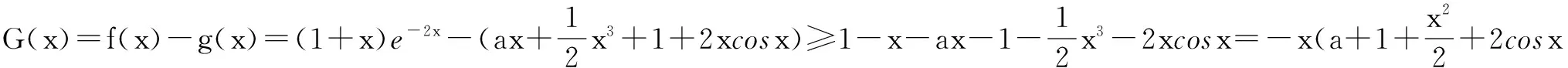
下面证明当a>-3时，f(x)≥g(x)在[0,1]上不恒成立.

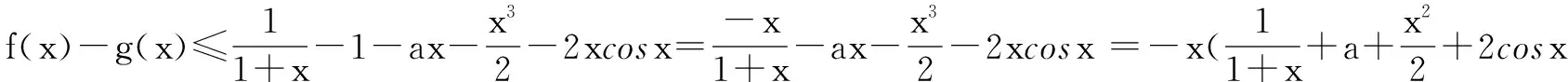
启示：通过四种求参方法的分析，笔者认为解决这类题目应注意以下几个方面.

1.培养学生敏锐的数学观察能力与过硬的运算能力

运算能力是思维能力与运算技能的结合，对高考而言，离开运算谈数学题目的解题思路与解决方法是没有意义的．一般来说，运算通畅说明解题方法选择正确，运算受阻时往往会对解题方法有所怀疑.所以，当解题方法正确时，过硬的运算能力就成为解题的保障.

2.培养学生解后反思的习惯

解后反思可以加深对题目的理解，提高解题的质量.解后反思重在反思解题切入点与解题细节.解题的切入点说到底是就解题方法的选择，决定了解题的成败.解题细节组成了解题过程，对解题细节反思，是因为每一个解题细节都决定了解题方向.

3.培养学生灵活的数学思维

每一道数学题目总有适合它的最优解法，而一种数学思想方法并不一定适用于一类题目，这就需要培养学生灵活的数学思维.对于一类数学题目，不能过份的依赖一种解题方法，以免形成非良性思维定势.

[1]苏凡文，高中数学中分离技巧的应用[J].中学数学研究，2015(08).

[责任编辑：杨惠民]

2017-05-01

岳茂富(1974.11-)，男，山东省泰安市宁阳县人，中学一级，本科,从事中学阶段的解题方法与课程改革研究.

G632

B

1008-0333(2017)16-0038-02