例谈妙用函数型不等式巧解导数压轴题
广东省佛山市第一中学(528000) 吴统胜 吴欣婷(学生)
例谈妙用函数型不等式巧解导数压轴题
广东省佛山市第一中学(528000) 吴统胜 吴欣婷(学生)
在利用导数证明函数导数压轴题中,有几个函数型不等式比较重要且较常见,恰当地利用这几个不等式,可以解决很多函数和数列不等式压轴题的证明问题.高考试题函数导数压轴题命题常常围绕着函数f(x)=ex,g(x)=lnx出题,究其主要原因有三:首先,此类函数的导数可以和多项式函数结合到一起,大部分都含有二次三项式,便于分类讨论,体现转化与化归思想;其次,此类函数更能体现微积分的一个思想:以直代曲,无限逼近.另外,此类函数也与高等数学中的级数有关,结合比较紧密.比如几个函数的麦克劳林级数为:
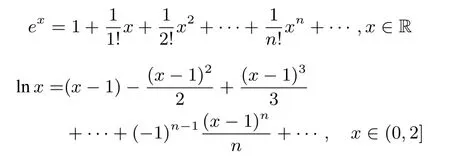
常见函数型不等式主要有以下三种类型:
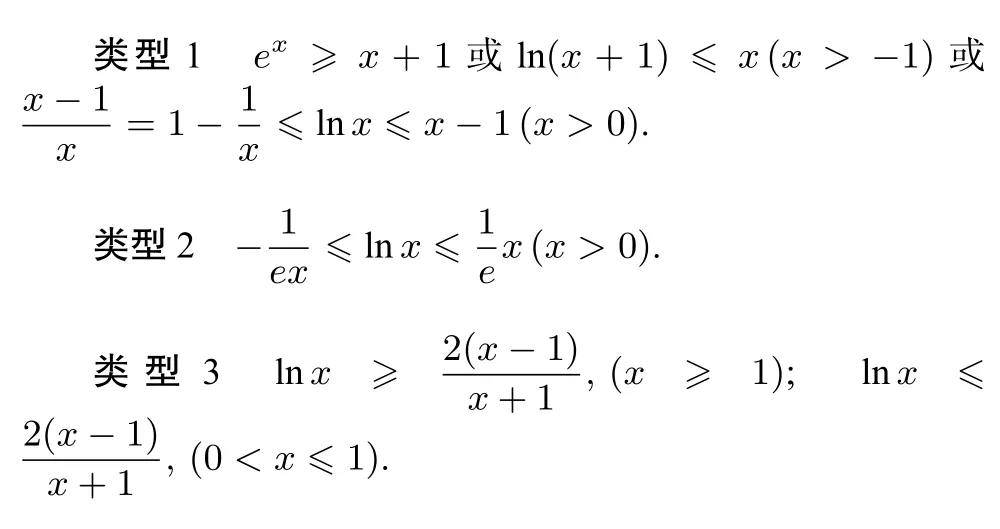
下面本文举例说明巧用常见函数型不等式妙证部分函数不等式压轴题,给出了y=ex,y=lnx,y=xlnx(x>0)放缩为一次函数形式的一般类型,对不能用函数型不等式证明的也进行了方法的优化、拓展,并对该部分内容复习备考给出了几点建议!
一、利用函数型不等式1
exx+1或ln(x+1)x(x> −1)或=1−lnxx−1(x>0)(见人教版教材《选修2-2》第32页习题1.3B组第1题),可结合图1加深对不等式的理解记忆.
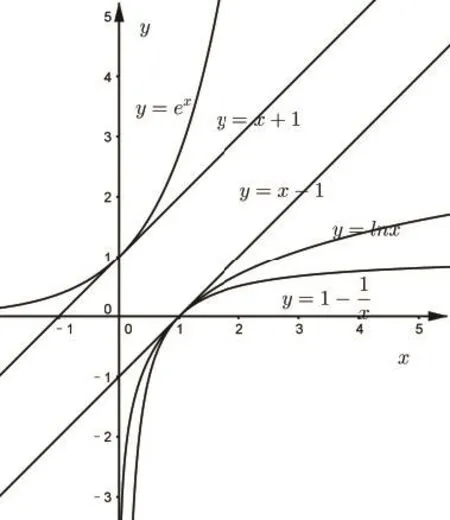
图1
例 1 (2013年课标 II理科 21)已知函数f(x)=ex−ln(x+m),
(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(2)当m 6 2时,证明:f(x)>0.
解析 (1)略.(2)当m 6 2时,f(x)=ex−ln(x+m)>ex−ln(x+2).
证法一 构造函数ϕ(x)=ex−ln(x+2),转化为求ϕ(x)min= ϕ(x0)>0,ϕ′(x)=在 (−2,+∞)上单调递增. 又 ϕ′(−1)<0,ϕ′(0)>0,所以 ϕ′(x)=0在 (−2,+∞)上有唯一实根 x0,且 x0∈ (−1,0).当x ∈ (−2,x0)时,ϕ′(x)<0;当 x ∈ (x0,+∞)时,ϕ′(x0)>0,所以 ϕ(x)min= ϕ(x0)由 ϕ′(x0)=0得:
ln(x0+2)=−x0,所以ϕ(x0)>0,所以f(x)>ϕ(x0)>0.所以当m 6 2时,f(x)>0.
但若妙用函数型不等式:ex>x+1及lnx 6 x−1(x>0),则证明过程相当简便,其证明过程如下:
证法二因为lnx 6 x−1(x>0),所以ln(x+2)6 x+1当且仅当x= −1时取等号,又因为ex>x+1当且仅当x=0时取等号,所以f(x)=ex−ln(x+m)>ex−ln(x+2)>x+1−(x+1)=0.由于两等号不同时取得,因此当m 6 2时,f(x)>0.
例2 (2016年广州一测理科21)已知函数f(x)=ex+m−x3,g(x)=ln(x+1)+2.
(I)若曲线y=f(x)在点(0,f(0))处的切线斜率为1,求实数m的值;
(II)当m>1时,证明:f(x)>g(x)−x3.
解析(I)略.(II)证法一:因为f(x)=ex+m−x3,g(x)=ln(x+1)+2,f(x)>g(x)−x3等价于ex+m−ln(x+1)−2>0.构造函数
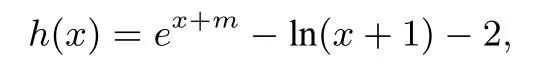
转化为证明h(x)min=h(x0)>0.但由于h(x0)=ex0+m−ln(x0+1)−2=0是超越方程,对应的x0难以解出.以下利用零点存在定理,采用设而不求法得最小值h(x0).由于

所以函数p(x)=h′(x)在(−1,+∞)上单调递增.又m>1,所以h′(0)=em− 1>0. 故函数 h′(x)在 (−1,+∞)上有唯一零点 x0,且 x0∈ (−1+e−m,0).因为 h′(x0)=0,所以即ln(x0+1)= −x0−m.当x∈(0,x0)时,h′(x)<0;当 x ∈ (x0,+∞)时,h′(x)>0.从而 h(x)的最小值为h(x0).故
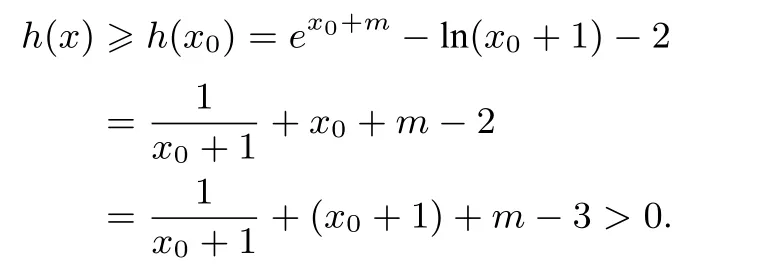
点评此方法转化为求函数的最小值,思路虽简单,但由于最小值h(x0)对应的x0不可求,需利用函数零点存在定理及设而不求法才可以较巧妙地解决证明问题,对思维及转化能力的要求相当高.但若妙用函数型不等式:ex>x+1(x∈R)及ln(x+1)6 x(x>−1),则证明过程相当快捷简便.
证法二先证明ex>x+1(x∈R),且ln(x+1)6 x(x> −1).设 F(x)=ex−x−1,则 F′(x)=ex−1.当x<0时,F′(x)<0;当 x>0时,F′(x)>0,所以 F(x)在(−∞,0)上单调递减,在(0,+∞)上单调递增.所以当x=0时,F(x)取得最小值F(0)=0.所以F(x)>F(0)=0,即ex>x+1(x∈R).所以ln(x+1)6 x(当且仅当x=0时取等号).再证明ex+m−ln(x+1)−2>0.由ex>x+1(x∈R),得ex+1>x+2(当且仅当x=−1时取等号).因为x>−1,m>1,且ex+1>x+2与ln(x+1)6 x不同时取等号,故
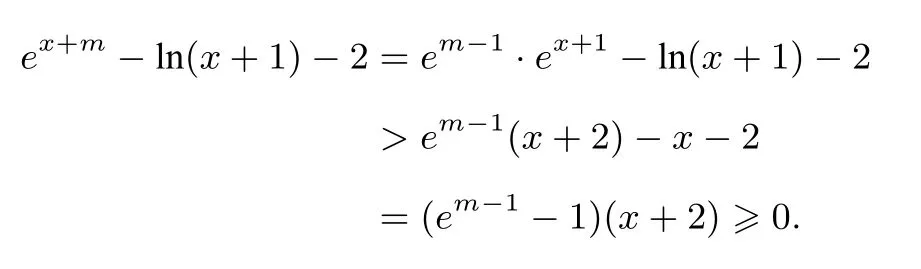
综上可知,当m>1时,f(x)>g(x)−x3.
二、妙用函数型不等式2
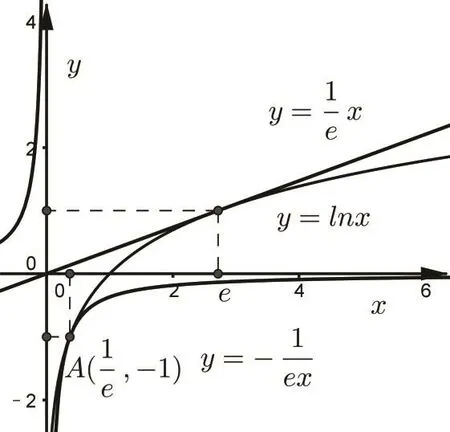
图2
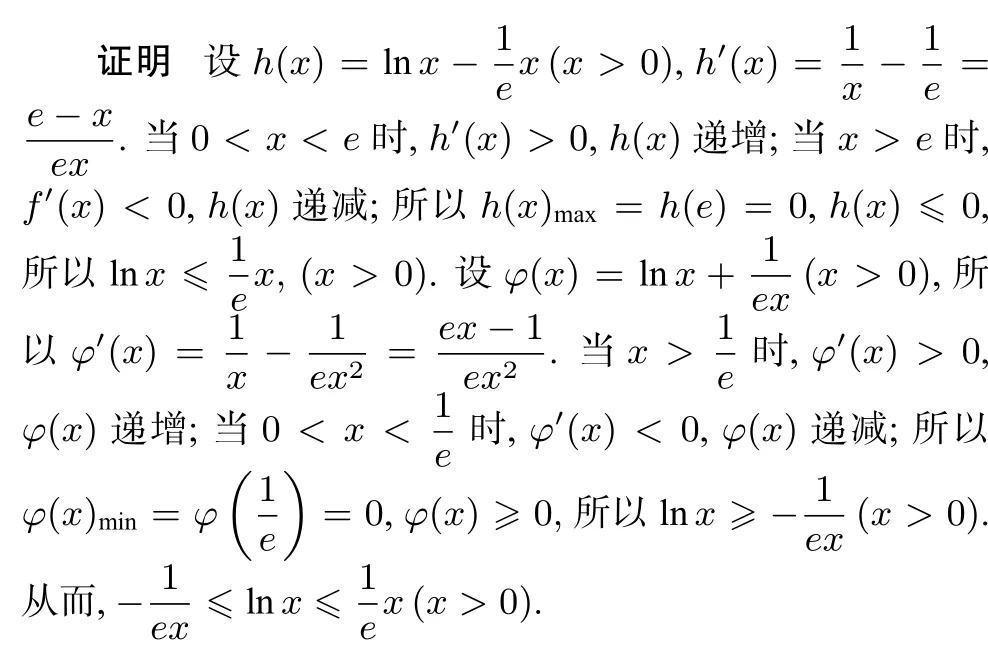
例3 (2017年佛山二模理科21)设函数f(x)=aex−xlnx,其中a∈R,e是自然对数的底数.
(I)若函数f(x)是(0,∞)上的增函数,求实数a的取值范围;
解析(I)略.(II)证法一:
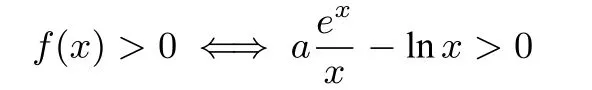
时,F(x)min>0,......
余下需要对x就0
证法二因为

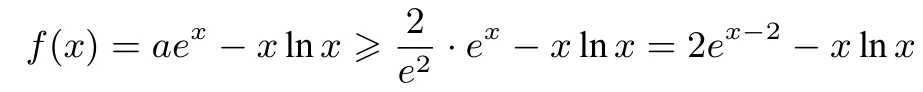
要证f(x)>0即证明:


当 0
点评 本题也可用构造函数法证明,对要证不等式进行适当变形,即证明:(x>0)设易证 φ(x)min=h(x)max=φ(x)min>h(x)max,故原不等式得证!
(I)若函数f(x)有零点,求实数a的取值范围;
解析(I)略.(II)当时即证:f(lnb)设 t=lnb(因为 b>1)即证:即证:,因为

当且仅当t=1时取等号,又因为

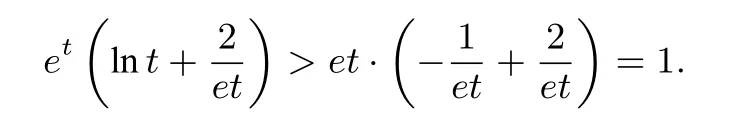
点评解决问题的关键首先在于通过换元转化为证明不等式f(t)=(t>0),再结合不等式结构特征巧妙利用函数型不等式和即可得证!本题证明也可用构造函数法证明,将要证不等式进行适当变形,将不等式两边分别转化为两个函数,通过比较这两个函数的最大值、最小值得证.这类同时含有ex,lnx的不等式有时可采用该方法.以上两题类同2014年全国I理科第21题.
三、妙用函数型不等式3
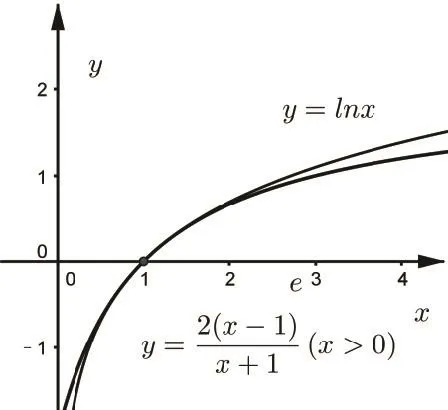
图3

点评 对于二元不等式类型,多采用二元化一元,再恰当构造函数证明不等式.该不等式可称之为对数基本不等式.类似地可证明:已知函数f(x)=lnx(x>0)则有
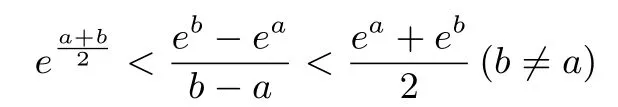
该不等式也可称之为指数基本不等式.
例6 (2013陕西理科21题)已知函数f(x)=ex,x∈R
(I)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值;
(II)设x>0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数.
解析(I)(II)略.(III),其证明如下:要证
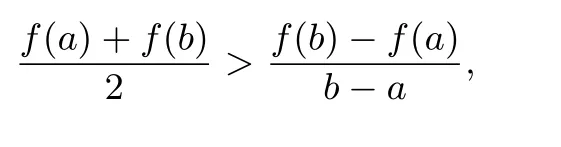
即证:
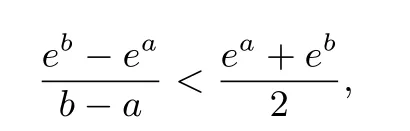
又因为a 设m=ea,n=eb,因为 b>a,所以 n>m>0则a=lnm,b=lnn,即证: 即证: 总之,同时含有ex,lnx的函数不等式的证明常可利用以上几类常见函数型不等式进行适当转化变形得证!也可以构造函数法证明,即将要证不等式进行适当变形为f(x)>g(x),记函数y=f(x),y=g(x),转化为证明f(x)min>g(x)max. 进一步的问题是:若f(x)min 下面通过例1举例说明利用”公切线”法证明此类不等式的基本步骤. 利用”公切线”法证明不等式 例7 (2013年课标II理科21)已知函数f(x)=ex−ln(x+m). (1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性; (2)当m 6 2时,证明:f(x)>0. 解 设 φ(x)=ex,h(x)=ln(x+2)的公切线为y=kx+b.设两切点分别为:M(m,em),N(n,ln(n+2)).利用切线的斜率得: 化简得: 得n+1=(n+1)ln(n+2),故n= −1或n=e−2;当n=−1时,M(0,1),N(−1,0),对应公切线为y=x+1. 点评利用”公切线”法证明函数型不等式,方法相当精妙!可实现精准放缩,证明方向也相当明确.但此方法只适用于一凸、一凹函数类型,若两函数同为凸函数或凹函数,可对不等式作适当变形,转化为一凸、一凹函数类型,再用”公切线”法证明. 常见的y=ex,y=lnx,y=xlnx我们可以放缩为如下一次函数形式(可用构造法或切线系证明,具体过程此处省略): 我们可把以上的放缩形式称为此类函数放缩的“一般式”!笔者已另外撰文详细举例说明这几个放缩式的应用,可以说该放缩法是快速解决函数不等式压轴题的通性通法之一! 全国课标卷“导数在研究函数中的应用”解答题以多项式函数(一次函数、二次函数、三次函数)、指数函数与对数函数的组合表达式为载体,设问方式都是考生熟悉的问题类型(切线问题、单调性问题、极值问题、最值问题、零点问题、恒成立问题、证明不等式问题),重点考查函数的单调性、极大(小)值、最大(小)值、函数的零点及不等式证明等主干内容,注重函数与方程、转化与化归、分类讨论、数形结合等思想方法的灵活运用,注重考查考生的数学思维能力和创新意识.因此,复习中要注重如下几点: 1.突出主干知识. 导数试题注重对导数的几何意义、导数的运算法则、导数在研究函数中的应用等重点内容的考查.因此,要熟练掌握求导公式与求导法则,深化对函数单调性的认识;要通过有效的变式训练,形成导数知识的结构网络. 2.注重综合. 深入研究三个二次之间的关系,加强方程根的分布和方程有解问题的研究;利用导数知识深刻认识三次函数的对称中心、零点、极值和最值;函数单调性是核心性质,单调性的复习应注重导数法的应用. 3.提炼方法. 复习中要提炼导数问题的数学思想方法,注重运用转化与化归、数形结合、分类讨论等思想方法处理导数问题. 4.提升能力. 由于函数与导数的解答题经常是压轴题,综合性强,难度较大,注重考查理性思维和创新意识,因此,在复习中要掌握解题思路的发现,强化转化意识,注重分类讨论,强化构造函数解决问题的方法.从对教材中基本初等函数的组合(所谓函数的组合就是基本初等函数的和、差、积、商),利用导数研究好这些组合函数的图像与性质.如y=lnx+x,y=lnx−x,y=xlnx,,y=ex+x,y=ex−x,y=xex,等组合函数的图像与性质要熟练掌握. 2.求证:当x>0时,有ex>2x+lnx成立. [1]彭海燕.广东省佛山市二模数学分析报告.2017.4 [2]陈镇民.广东省广州市一模数学分析报告.2017.3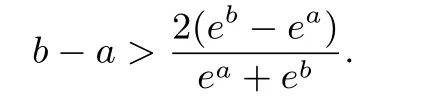
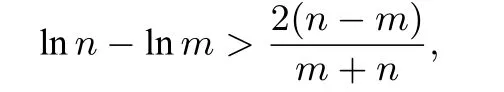

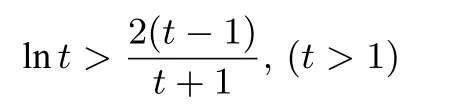
四、方法优化和拓展
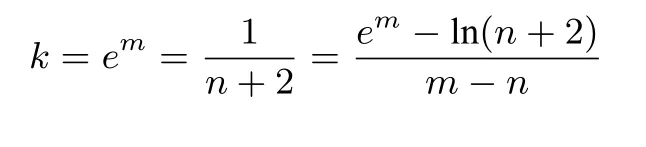
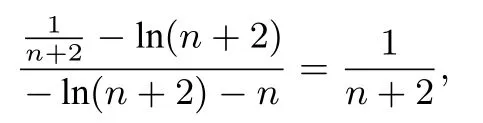
五、方法优化的再拓展

六、复习备考建议
七、反馈练习

