空间向量在立体几何中的应用
汕头市潮阳区棉光中学(515100) 黄桂南
空间向量在立体几何中的应用
汕头市潮阳区棉光中学(515100) 黄桂南
向量进入高中数学教材,为用代数方法研究几何问题提供了强有力的工具,促进了高中几何的代数化.向量是几何的,又是代数的,可以直接描述、想象、替代立几中的点、线、面等对象,又可以通过向量的计算,对它进行加、减、乘、数乘、数量积,丰富了立体几何的运算模式,使立体几何中的抽象概念有了具体的形式,让学生可以更直观地观察到立体几何中各种位置关系的性质,能更加深刻理解立体几何中的定理,有利于学生突破空间向量想象力薄弱的学习难点,同时以运算为载体,发挥空间想象力就可以对立体几何中的角度、距离问题进行实际运算与演绎.这就为空间想象能力较弱的学生解题提供了新的出路,降低了其学习的难度,提高了学生的学习兴趣.
立体几何是高中数学的重点和难点之一,很多学生一提到立体几何就会“谈虎色变”,教师也普遍认为立体几何教学是吃力不讨好的事.向量法正是解决这一现实问题的行之有效的方法.立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等.其中比较多的主要是用向量证明线线、线面垂直及计算空间角与空间距离.下面我主要就近年国卷高考题来举例其应用,希望能起到一个抛砖引玉的作用.
一、建立坐标系的常用方法
我们通过一个高考试题的立几问题的例子总结建立空间直角坐标系的一般方法.
例1(2015高考新课标 1,理 18)如图,四边形ABCD为菱形,∠ABC=120◦,E,F 是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
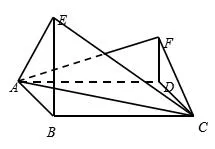
图1
(1)证明:平面AEC⊥平面AFC
(2)求直线AE与直线CF所成角的余弦值.
试题分析理数第二问一般考查角度问题,多用空间向量解决,关键是正确建系.本题正是利用“菱形对角线互相垂直”找到底面直角建系.
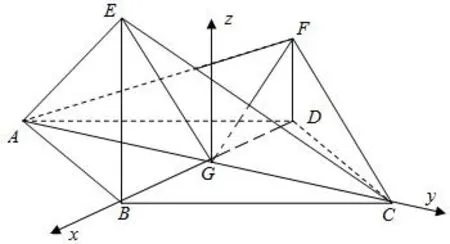
图2
(I)连接BD,设BD∩AC=G,连 接 EG,FG,EF,在菱形ABCD 中,不 妨设GB=1易证EG⊥AC,通过计算可证EG⊥FG,根据线面垂直判定定理可知EG⊥平面AFC,由面面垂直判定定理知平面AFC⊥平面AEC.(也可以先建空间直角坐标系由两个平面的法向量互相垂直去证明两个平面垂直.)
建系原则遵循“右手原则”,如下图用常见正方体举例.
图3
1)直接运用现有的垂直关系建系,如正方体、长方体、直棱柱等.
2)利用性质关系建系,如等腰三角形、菱形对角线、正棱锥等.
3)利用题中的已知条件建系,如点在平面内的射影在某条直线上.
4)若没有以上三种关系,则先确定底面“直角”,再建系.
总之,一定要选取适当的坐标原点及坐标轴,使得数值计算更简洁,有利于提高解题效率.
二、应用空间向量求解立体几何中的空间角问题
1.求异面直线所成的角
分别在直线m,n上取两个定向量a,b,则异面直线m,n所成的角β等于向量a,b所成的角或其补角θ,则cosβ =|cosθ|=特殊情形:a⊥b ⇐⇒ a·b=0,即异面直线a垂直于b.
例2(2014新课标2,理11)直三棱柱ABC−A1B1C1中,∠BCA=90◦,M,N 分别是 A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成的角的余弦值为( )
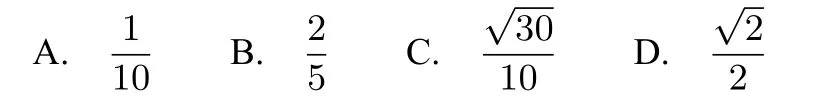
解析以C为原点,直线CA为x轴,直线CB为 y轴,直线 CC1为 z轴,则设 CA=CB=1,则B(0,1,0),M,故=所 以 cos=,故选C.

评注应用空间向量法解此类题避开了作平移及复杂的逻辑推理.
2.求直线与平面所成的角
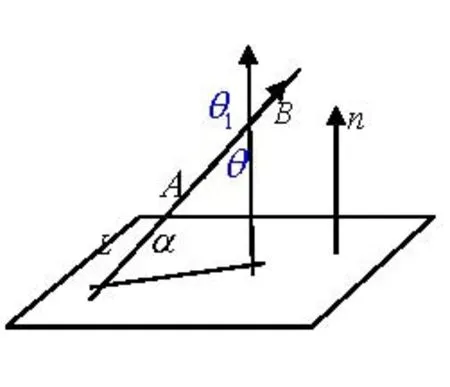
图4
例3(2013新课标1,理18)如图,三棱柱 ABC−A1B1C1中,CA=CB,AB=AA1,∠BAA1=60◦.
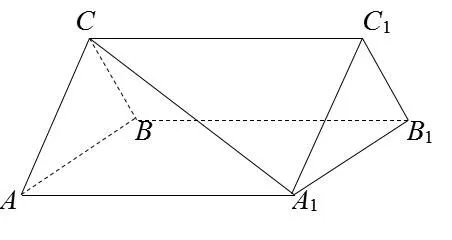
图5
(I)证明AB⊥A1C;
(II)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
解析(1)取AB的中点O,连接OC、OA1、A1B,因为CA=CB,所以 OC⊥AB,由于 AB=AA1,∠BAA1=60◦,故△AA1B为等边三角形,所以OA1⊥AB,所以AB⊥平面OA1C,因为A1C⊂平面OA1C,所以AB⊥平面A1C;
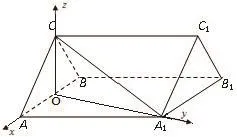
图6
(2)由 (1)知 OC⊥AB,OA1⊥AB,又 平 面 ABC⊥ 平面,故OA,OA1,OC两两相互垂直.以O为原点,OA为x轴,OA1为 y轴,OC 为 z轴,为单位,建立如图所示的空间直角坐标系O−xyz.由题设知A(1,0,0),(x,y,z)为平面BB1C1C的法向量,则,即所以n=设直线A1C与平面BB1C1C所成角为α则:sinα所以直线A1C与平面BB1C1C所成角的正弦值
评注找直线的方向向量与平面的法向量,转化为向量的夹角问题,注意线面角与两向量所在直线夹角互余.
3.求二面角
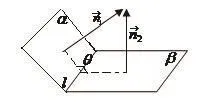
图7
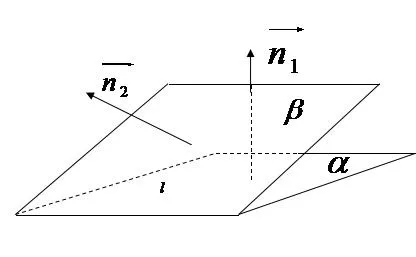
图8
方法一构造二面角α−l−β的两个半平面α,β的法向量n1,n2(都取向上的方向,如图7所示),则
①若二面角α−l−β是“钝角型”的如图8,那么其大小等于两法向量的夹角的补角,即cosθ=
②若二面角α−l−β是“锐角型”的如图9,那么其大小等于两法向量的夹角,即cosθ=
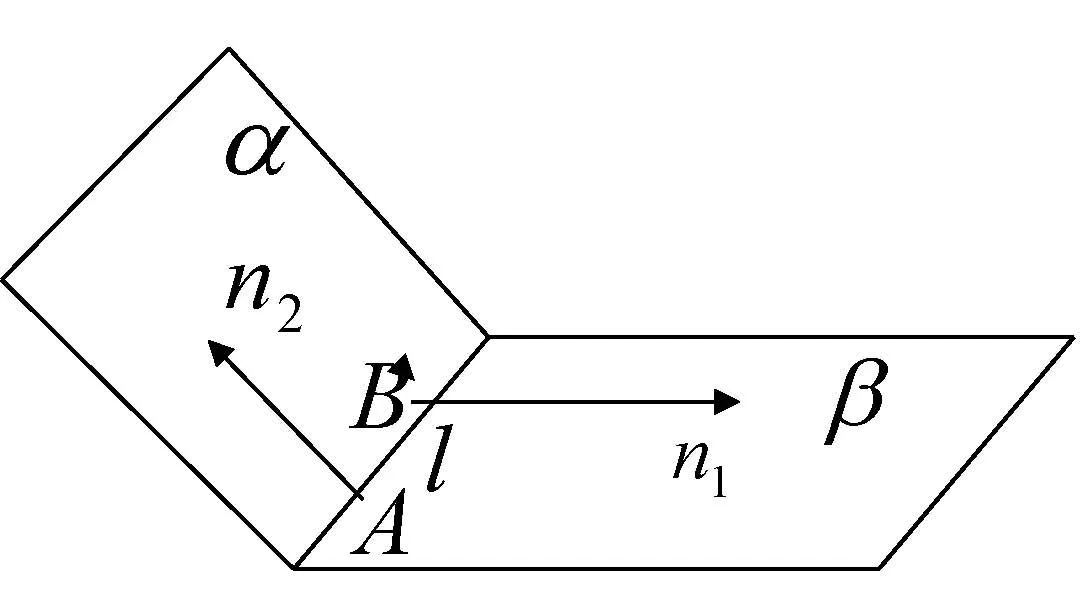
图9
方法二在二面角的棱l上确定两个点A,B,过A,B分别在平面α,β内求出与l垂直的向量n1,n2,则二面角α−l−β的大小等于向量n1,n2的夹角,即cosθ=
说明通过法向量的方向来求解二面角,两个法向量的方向是“一进一出”,所求的二面角的平面角就等于两法向量的夹角,如果是“同进同出”,所求的二面角的平面角就等于两法向量的夹角的补角.
以上方法在处理二面角是锐角还是钝角问题时,可能会遇到方向判断困难问题,所以在计算之前不妨先依题意直观判断一下所求二面角的大小,然后根据直观图取“相等角”或取“补角”.
以上方法在处理二面角问题时,可能会遇到二面角的具体大小问题,所以在计算之前不妨先依题意直观判断一下所求二面角的大小,然后根据计算取“相等角”或取“补角”.
例4(2016新课标1,理18)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90◦,且二面角D−AF−E与二面角C−BE−F都是60◦.

图10
(I)证明:平面ABEF⊥平面EFDC;(II)求二面角E−BC−A的余弦值.
解 (I)由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC.又AF⊂平面ABEF,故平面ABEF⊥平面EFDC.
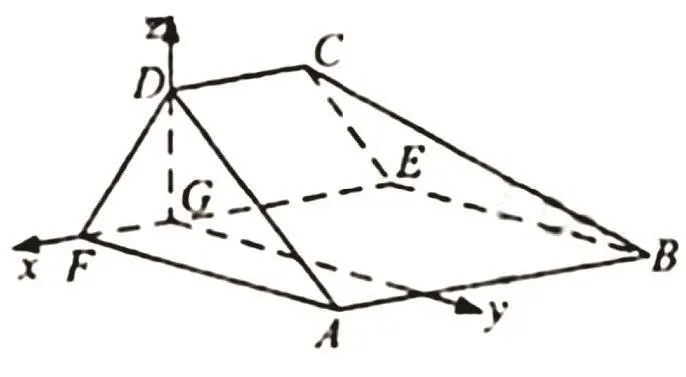
图11
(II)过 D 作 DG⊥EF,垂足为G,由(I)知DG⊥平面ABEF.以 G 为坐标原点,的方向为x 轴正方向,为单位长,建立如图所示的空间直角坐标系G−xyz.由(I)知∠DFE为二面角 D−AF−E的平面角,故 ∠DFE=60◦,则 |DF|=2,|DG|=3,可得 A(1,4,0),B(−3,4,0),E(−3,0,0),D.由已知,AB//EF,所以AB//平面EFDC.又平面ABCD∩平面EFDC=DC,故AB//CD,CD//EF.由 BE//AF,可得 BF⊥平面 EFDC,所以∠CEF为二面角C−BE−F的平面角,∠CEF=60◦.从而可得√设 n=(x,y,z)是平面BCE的法向量,则可取n=.设m是平面ABCD的法向量,则,同理可取m=.如图二面角的平面角为钝角,则cos⟨n,m⟩=.故二面角E−BC−A的余弦值为
例 5(2014新 课标1,理19)如图三棱柱 ABC−A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

图12
(I)证明:AC=AB1;
(II)若AC⊥AB1,∠CBB1=60◦,AB=BC,求二面角A−A1B1−C1的余弦值.
证明(I)连接BC1,交B1C于点O,连接AO,因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.AB⊥B1C,所以B1C⊥平面ABO.由于AO⊂平面ABO,故B1C⊥AO.又 B1O=CO,故AC=AB1.
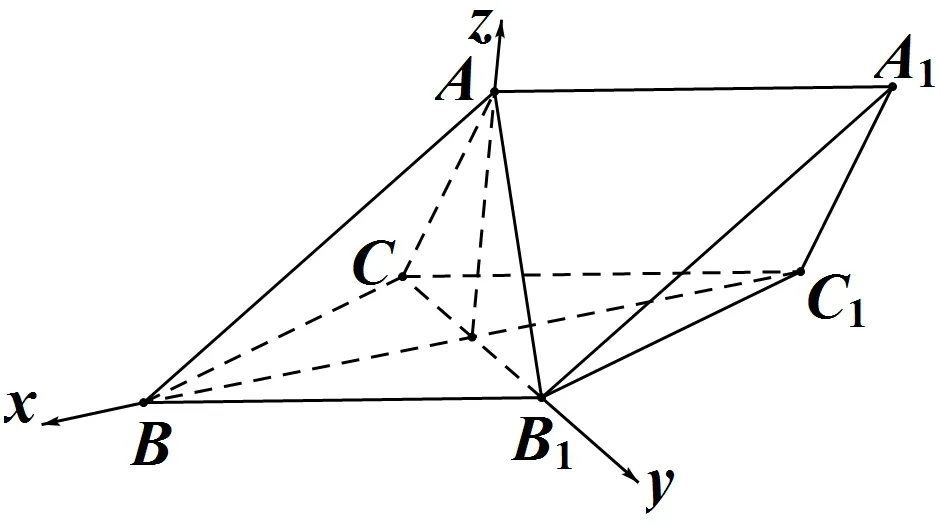
图13
(II)因为AC⊥AB1,且O为B1C的中点,所以AO=CO.又因为AB=BC,所以△BOA ∼= △BOC,故 OA⊥OB,从 而OA,OB,OB1两两相互垂直以O为坐标原点,OB为x轴,OB1为 y轴,OA 为 z轴,|−−→OB|为单位长度,建立如图所示的空间直角坐标系O−xyz.因为∠CBB1=60◦,所以△CBB1为等边三角形.又AB=BC,则A设n=(x,y,z)是平面AA1B1的法向量,则即所以可取n=.设m是平面A1B1C1的法向量,则同理可取 m=如图二面角的平面角为锐角,则cos⟨n,m⟩=.所以二面角A−A1B1−C1的余弦值为
评注 1)应用空间向量法解此类题避开了找二面角的平面角及复杂的逻辑推理,只须求出两个半平面的两个法向量,应用向量内积即可求二面角.所以求二面角的关键在于找到两个半平面各自的一个法向量,在利用公式即可.
2)大多数情况下,两个半平面的两个法向量n1,n2一个是显向量,一个是隐向量.显向量可直接写结果,而隐向量需要求.
3)如果能用常规法较容易求出二面角的平面角,则用常规法求解.
异面直线所成的角、直线与平面所成的角和二面角是立体几何中空间角的三种类型.传统综合推理法的三步是“作— 证— 算”,但作这几个角的过程对空间想象能力和逻辑推理能力的要求比较高,而利用向量法解此类问题就可以避开抽象、复杂地寻找角的过程.只要能够熟练应用公式,就可以避烦就简,从而顺利地解决问题.
三、应用空间向量求解立体几何中的空间距离问题
1.点到点、点到线的距离
2.求点到平面的距离(推广到线面、面面之间的距离)

图14
方法如图,易知:点P到平面 α的距离 d=cosθ,而 cosθ=,所以 d=其中n是平面α的一个法 向 量,是 平 面 α 的 斜 向 量 则点P到平面α的距离d等于在n上的射影长,即点P到平面α的距离为:
例6如图,在三棱椎P−ABC中,平面ABC,D,E,F分别是棱 AB、BC、CP的中点,AB=AC=1,PA=2,
(I)求直线PA与平面DEF所成角的大小;
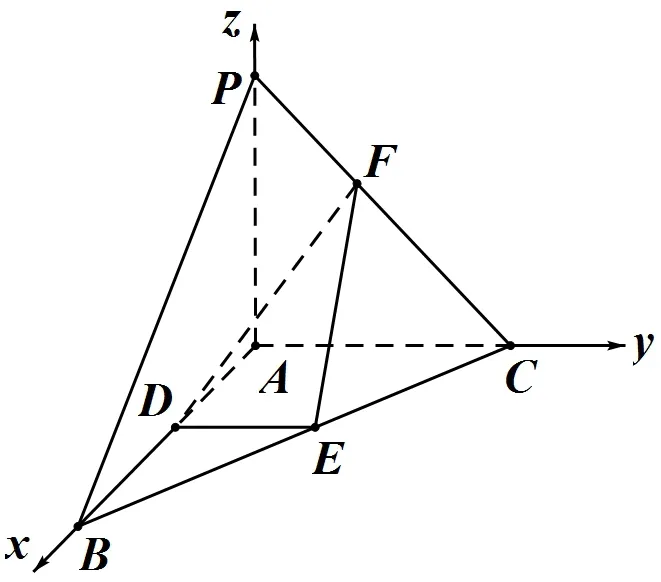
图15
(II)求点P到平面DEF的距离.

评注求点到平面的距离,关键是找到平面的法向量及这点与平面内一点构成的向量.我们利用这公式,不仅可解决点到平面的距离,还可推广到直线与平面的距离,平行平面间的距离问题.
3.求异面直线距离
方法如图,d是异面直线a与b的距离,是直线a与b的一个法向量A、B分别是直线a,b上的点,显然:又 cosθ =,所以 d=
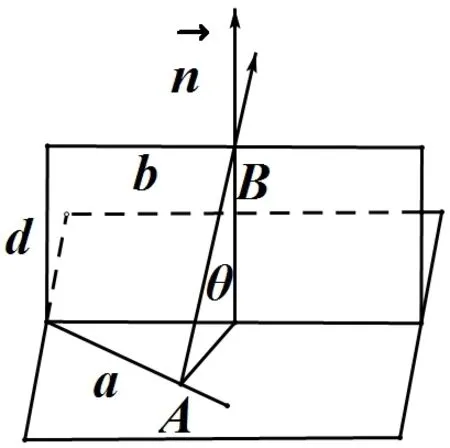
图16
例7如图,在正三棱柱A1B1C1−ABC中,D,E分别是棱 BC、CC1的中点,AB=AA1=2,求异面直线AB1与BE的距离.
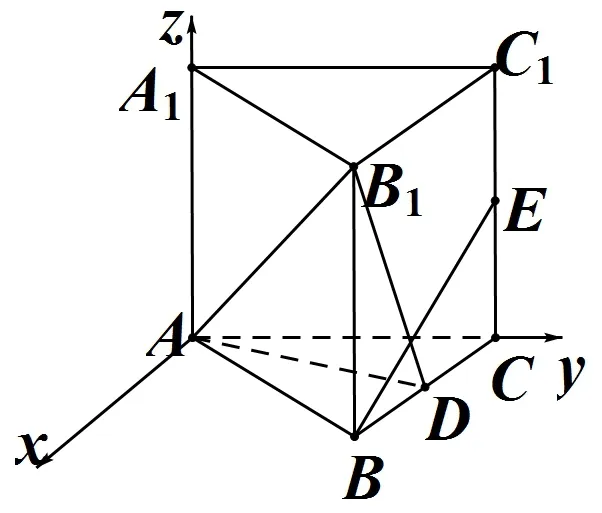
图17
解如图建立空间直角坐标系设n=(x,y,z)是AB1与BE的法向量,又因为=,可得:则取 y=3,可知n=(0,0,2),所以 d=
评注求异面直线的距离,关键在于求出异面直线的一个公共法向量和与两异面直线相交的线段的向量.
四、向量法解决立体几何问题的步骤
用向量法解决立体几何问题的方式有两种:一是直接用向量的代数式运算,二是用向量的坐标运算.一般来说,向量的坐标运算,思维量更少,运算技巧更低,更容易掌握,因此这也是我们常用的向量方法.若所给图形不容易建立空间直角坐标系,我们也可以用向量的代数式运算来解决问题,但其技巧性相对较高,对学生逻辑推理能力的要求也提高了.用向量坐标运算解题步骤:
(1)建立空间直角坐标系.注意尽可能用已经存在的过同一个点的两两垂直的三线,如果没有三线,也尽量找两线垂直,然后作出第三线和两线垂直,按右手系建立坐标系.注意所写点的坐标要与所建立的坐标系相一致.
(2)写出需要用到的点的坐标.注意要仔细再仔细,此步若错,全题皆错.
(3)写出所要用到的向量坐标.注意必须终点坐标减始点坐标.
(4)通过计算解决具体问题.注意公式要记对,运算要仔细.
向量在立体几何中的应用为我们解决立体几何问题提供了新的解题思路和方法,打破了传统解法“一作、二证、三计算”的模式,突破了传统解法中“添置辅助线”的难点,将立体几何中“形”的问题转化为“数”的问题,开创了解决立体几何问题的新模式.
五、“向量法”在立体几何教学中的教学策略
(1)强化空间向量的教学
向量运算可以有效地将代数问题和几何问题进行相互转化,实现数与形的统一,是数形结合的典型,从而解决相关立体几何问题,“向量法”作为解决立体几何问题有效工具,尤其是那些综合性较强的题型,利用“向量法”可以很好地将问题转化,在立体几何问题中运用向量运算避免学生对图形的逻辑思考,从而降低学生对立体几何图形的空间想象难度.
教师通过强化对学生的“向量法”教学,可以帮助学生就数与形的关系建立正确的认识,体验立体几何图形的创造过程,利用代数方法处理几何图形的问题,塑造学生数形统一的思想方法,学生可以通过向量的运算,进而揭示立体几何图形之间的数量关系,解决立体几何问题.
(2)加深学生对公式的理解
“向量法”运算公式很多是和学生之前学习的知识有很大区别的,学生对这些“变形”公式比较陌生,因为对公式不熟悉,很多学生都是死记硬背,很可能对公式的遗忘,这样在运用过程中就会出现很大的问题,这对应用“向量法”是非常不利的.因此在教学中,教师应尽可能地加深学生对公式的理解,让学生知道向量公式的来源,公式怎么用等,构建向量知识的内在联系以及向量和其他知识点的联系,让学生形成对“向量法”公式的理解记忆,时而灵活运用公式.
(3)对比综合法与向量法的利弊
综合法-不使用其他工具,对几何元素及其关系直接进行讨论.其优点是注重培养学生的空间想象能力、逻辑推理能力以及转化化归的数学思想.缺点是有时解决问题时的技巧性过强,而且没有一般规律可循,常常让学生感觉“高不可攀”,从而“望而却步”.
向量法-以向量和向量的运算为工具,对几何元素及其关系进行讨论.其优点是注重培养学生的数形结合、转化化归的数学思想以及代数计算能力的同时也使立体几何问题的解决过程变得数量化、程序化,易于学生学习.缺点是计算量相对较大,对于计算能力较弱的学生,很容易算错.
如果学生在解决立体几何问题时,能够具体情况具体分析,将综合法与向量法这两种方法综合运用,那样将会使得立体几何问题得到更完美的解决.
六、教学实践成果
在课题研究过程中,我们以教师自编教、学案的模式,分别在两个研究阶段共开设了16节公开课、观摩课,针对2016年的全国卷备考方向,以立体几何中的“三大角度”求解为主要核心内容,开展教学实践研究,其中同时对高二理科两个教学班开展“同课异构”对比式的教学实验,在教学实践中进一步验证研究的理论成果.通过对比式教学模式及课后的教学效果反馈,我们发现,高二理科实验班在使用了“向量法”的教学后,相比普通班的“综合法”教学,实验班的学生学习兴趣、学习效果有明显的提高,成绩的优秀率达到30%,明显优于普通班.另一方面,“学案”为辅助的课堂教学使学生的学习方式得到了较大的转变,增强了学生学习的主动性,提高了学生的学习兴趣及数学运用意识,逐渐地学会用“向量法”解决“三大角度”问题的方法,并将“向量法”作为解决相关问题的工具.
综上所述,借助空间向量作为解题工具,解决高中数学立体几何中的空间角,空间距离的问题,显然与传统法相比有明显的优势,从学生的学习效果来看,学生较易于接受其解题原理,从根本上可以帮助学生克服空间想象力较弱的困难,但它也对学生的计算能力也需要有较高的要求,因此,在常规的课堂教学过程中,在巩固学生对空间向量概念的理解的基础上,必须通过有效的训练逐步提高学生的计算能力.向量确实是解决立体几何、解析几何强有力的工具.所以在整个高中的数学学习中,如能学会用向量方法处理数学问题,这不仅可使相应问题的解法简洁漂亮、独特、一题多解,而且反复的应用能帮助学生深入理解向量概念,熟练掌握向量的运算,更能丛中学到数形结合、转化变形等重要的数学思想,能明显减轻学生和教师的负担.
因此,向量是解决立体几何问题的实用工具.
[1]林沛玉.运用向量的数量积解几何题[J].中学数学研究,2005(5)
[2]谢朝军.平面的法向量及其应用[J].中学数学研究,2006(4)
[3]陈升裕.向量在解立体几何题中的应用[J].中学数学研究,2007(5)
[4]崔敬赛,何小亚.2011年广东高考理科立体几何评[J].中学数学研究,2011(9)

