导数及其应用问题例析

河北 周 雪

导数及其应用问题例析

河北 周 雪

导数的应用十分广泛，如求函数的单调区间、极值、最值，求曲线的切线以及解决某些实际问题等．利用导数工具使复杂问题变得简单化，导数为研究函数的单调性及极值等问题提供了通用的解题思路和方法，因而已逐渐成为新高考的又一热点．高考对导数的要求主要表现在三个方面，即考查导数的概念、求导的公式和求导的法则；导数的简单应用，包括求函数的极值，求函数的单调区间，证明函数的增减性等；综合考查，包括解决应用问题以及有关导数内容的综合问题．

一、导数的几何意义

导数的实质是函数值相对于自变量的变化率，体现在几何上就是切线的斜率．利用导数的几何意义，研究曲线切线的斜率是导数的重要内容．求切线的方程可通过求导数先得到斜率，再由切点利用点斜式方程得到，求过点p（x0，y0）的切线方程时，一要注意p（x0，y0）是否在曲线上，二要注意该点可能是切点，也可能不是切点，因而所求的切线方程可能不止有1条．

【例1】已知曲线C：y＝x3－3x2＋2x，直线l：y＝kx，且l与C切于点（x0，y0）（x0≠0），求直线l的方程及切点坐标．

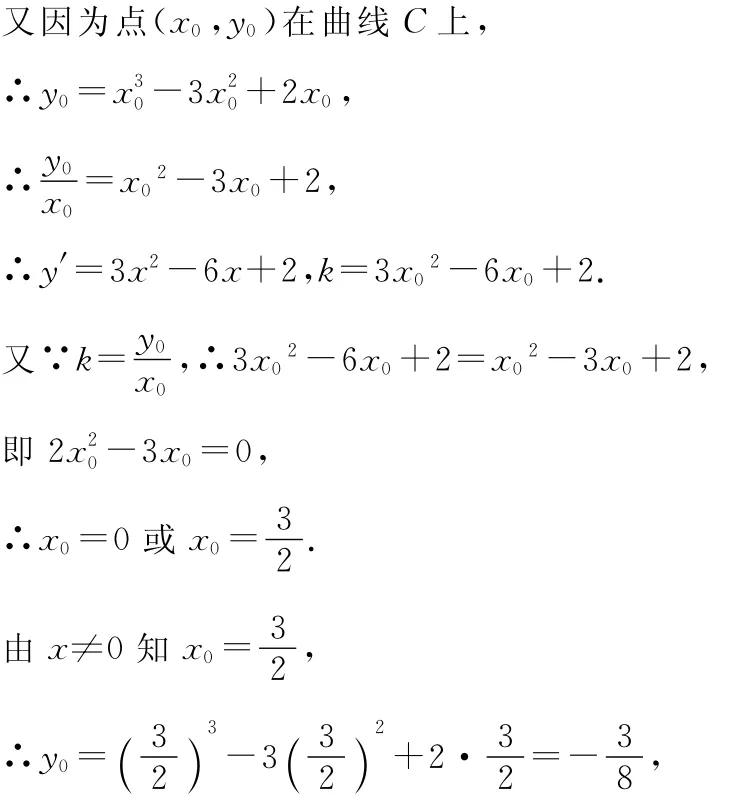
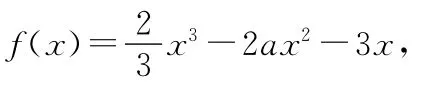
二、运用导数有关知识研究函数的单调性和最值（极值）问题

1．求函数单调区间的步骤：①确定函数的定义域；②求导函数f′（x）；③解不等式f′（x）＞0，得f（x）的递增区间；解不等式f′（x）＜0，得f（x）的递减区间．即函数的增区间是f′（x）≥0恒成立的区间，函数的减区间是f′（x）≤0恒成立的区间（其中导数值为零的点为有限个）．

利用求导方法讨论函数的单调性，要注意以下几方面：①在某个区间上f′（x）＞0（＜0）是f（x）在该区间上递增（递减）的充分条件而非必要条件；②求单调区间时，首先要确定定义域；然后再根据f′（x）＞0（或f′（x）＜0），解出在定义域内相应的x的范围．

（Ⅰ）判断f（x）的单调性；

令g（x）＝－ax2＋2ax－a－1．

①当a＝0时，g（x）＝－1＜0，∴f′（x）＜0，

∴f（x）在R上为减函数．

∴g（x）＜0，即f′（x）＜0

∴f（x）在R上为减函数．

③当a＜0时，由－ax2＋2ax－a－1＞0，

由－ax2＋2ax－a－1＜0，

（Ⅱ）①当a≥0时，f（x）在［1，2］上为减函数．

【解析】f′（x）＝x2－ax＋（a－1）．

由f′（x）＝0，得x1＝1或x2＝a－1．

当a－1≤1，即a≤2时，x∈（1，＋∞）时，f′（x）＞0，

所以f（x）在（1，＋∞）内递增，不合题意．

当a－1＞1，即a＞2时，x∈（1，a－1）时，f′（x）＜0；

x∈（a－1，＋∞）时，f′（x）＞0，

所以f（x）在（1，a－1）内单调递减；在（a－1，＋∞）内单调递增．

又由已知得x∈（1，4）时f′（x）＜0，x∈（6，＋∞）时f′（x）＞0，

∴4≤a－1≤6，即5≤a≤7．

2．求可导函数极值的步骤：①求导函数f′（x）；②求方程f′（x）＝0的根；③检查f′（x）在方程根左、右的符号，如果左正右负，那么f（x）在这个根处取得极大值；如果左负右正，那么f（x）在这个根处取得极小值．如果左右不改变符号，那么f（x）在这个根处无极值．

【例3】设x＝1与x＝2是函数f（x）＝alnx＋bx2＋x的值点．

（1）试确定常数a和b的值；

（2）试判断x＝1，x＝2是函数f（x）的极大值点还是极小值点，并说明理由．

【解析】

【变式】已知函数fx＝ax＋bx＋cx在点x0处取得极小值－4，使其导数f′（x）＞0的x的取值范围为（1，3），求f（x）的解析式．

【解析】由题意得：

3．利用导数求函数的最值时，首先求f（x）在（a，b）内的极值，然后将f（x）的各极值与f（a）、f（b）比较得出函数f（x）在［a，b］上的最值．具体可分为以下几步：①求出可导点，即f′（x）＝0的解x0；②用极值的方法确定极值；③将（a，b）内的极值与f（a）、f（b）比较，其中最大的为最大值，最小的为最小值；当f（x）在（a，b）内只有一个可导点时，若在这一点处f（x）有极大（小）值，则可以确定f（x）在该点处取到了最大（小）值．

（1）当a＝2时，求f（x）的极值；

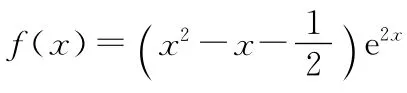
设f′（x）＝0得x＝±1，那么当x变化时f′（x）及f（x）变化情况如下表：

__x （－∞，－1） －1 （－1，1） 1 （1，＋∞）f′（x）＋____ ____0____ ____－____ ______0＋___ f（x） 极大值3________________________2e2 极小值－e22__ ________

令g′（x）＝（x－1）（ax＋2）eax＝0，

所以g（x）最小值为，解得0＜a≤ln3．

【变式】已知函数f（x）＝x3－ax2＋3x．

（1）若f（x）在x∈［1，＋∞）上是增函数，求实数a的取值范围；

（2）若x＝3是f（x）的极值点，求f（x）在x∈［1，a］上的最小值和最大值．

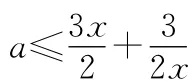
（2）由题意知f′（x）＝3x2－2ax＋3＝0的一个根为x＝3，可得a＝5，

又f（1）＝－1，f（3）＝－9，f（5）＝15，

∴f（x）在x∈［1，5］上的最小值是f（3）＝－9，最大值是f（5）＝15．

三、利用导数证明等式或不等式

利用导数证明等式或不等式为中学数学引进了新的思路和方法，在证明不等式或等式时，首先要构造函数和确定定义域，其次运用求导的方法来证明．

【例5】已知函数：f（x）＝alnx－ax－3（a∈R）．

（1）讨论函数f（x）的单调性；

（2）若函数y＝f（x）的图象在点（2，f（2））处的切线的倾斜角为45°，对于任意的t∈［1，2］，若函数g（x）＝x3＋在区间（t，3）上有最值，求实数m的取值范围；

（3）求证：ln（22＋1）＋ln（32＋1）＋ln（42＋1）＋…＋ln（n2＋1）＜1＋2lnn！（n≥2，n∈N＊）．

当a＜0时，f（x）的单调递增区间为［1，＋∞），单调减区间为（0，1］；

当a＝0时，f（x）不是单调函数．

由题意知：对于任意的t∈［1，2］，g′（t）＜0恒成立，

（3）令a＝－1（或a＝1），此时f（x）＝－lnx＋x－3，所以f（1）＝－2，

ln（22＋1）＋ln（32＋1）＋ln（42＋1）＋…＋ln（n2＋1）＜1＋2lnn！（n≥2，n∈N＊），

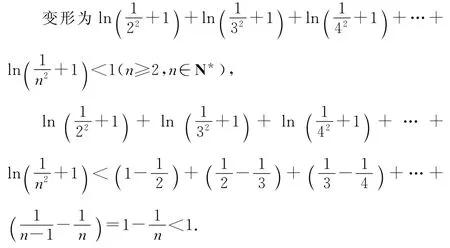
【变式】已知函数f（x）＝ex－ln（x＋1）－1（x≥0），

（Ⅰ）求函数f（x）的最小值；

（Ⅱ）若0≤y＜x，求证：ex－y－1＞ln（x＋1）－ln（y＋1）．

所以当x≥0时，f′（x）≥0，

则函数f（x）在［0，＋∞）上单调递增，

所以函数f（x）的最小值为f（0）＝0．

（Ⅱ）由（Ⅰ）知，当x＞0时，f（x）＞0，

四、导数在实际问题中的运用

导数在自然科学、工程技术等方面都有广泛的应用，解决实际应用问题关键在于建立数学模型和目标函数，把“问题情景”译为数学语言，找出问题的主要关系，并把问题的主要关系近似化，形式化，抽象成数学问题，再划归为常规问题，选择合适的数学方法求解．难点是如何把实际问题中所涉及的几个变量转化成函数关系式．

【例6】烟囱向其周围地区散落烟尘而造成环境污染．已知A、B两座烟囱相距3km，其中A烟囱喷出的烟尘量是B烟囱的8倍，经环境检测表明：落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比，而与烟囱喷出的烟尘量成正比（比例系数为k）．若C是连接两烟囱的线段AB上的点（不包括端点），设AC＝xkm，C点的烟尘浓度记为y．

（Ⅰ）写出y关于x的函数表达式；

（Ⅱ）是否存在这样的点C，使该点的烟尘浓度最低？若存在，求出AC的距离；若不存在，说明理由．

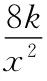
解得x＝2．

故当0＜x＜2时，y′＝0．当2＜x＜3时y′＞0．

可见当x＝2时，y取得极小值，且是最小值．

即在连接两个烟囱的线段AB上，距烟囱A处2km处的烟尘浓度最低．

【变式】在甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在此岸边合建一个供水站C，从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元，问供水站C建在岸边何处才能使水管费用最省？

导数是函数、解几的交汇点，有着重要的工具作用，丰富了对函数研究的方法，现在已是新高考重点考察的基础知识，成为高考数学的一大热点，相信高考仍然是会重点考查的，所以考生要引起高度的重视．

（作者单位：河北省衡水市第二中学）