不相容工件组的单机随机调度问题研究
谭 琦,王永青,戴 飞
(合肥工业大学 电气与自动化工程学院,合肥 230009)
不相容工件组的单机随机调度问题研究
谭 琦,王永青,戴 飞
(合肥工业大学 电气与自动化工程学院,合肥 230009)
研究不相容工件组在单台批处理机上的分批加工问题,工件具有随机的到达时间和加工时间。不相容工件组是指属于不同组的工件不能被安排在同一批中加工。首先,以长期平均代价最小为优化目标,以缓冲库中工件数为实时状态,建立了基于半马尔科夫决策过程的系统模型。然后,通过策略迭代算法对其进行优化控制,同时为了缓解大状态空间导致的维数灾问题,给出了基于模拟退火的Q学习算法。仿真实验验证了所提出方法的有效性。
不相容工件组;随机调度;批处理机;Q学习
0 引言
实际生产环境由于受到多种不确定性或随机性因素的影响,调度信息通常无法提前准确预知。为了克服不确定性对系统决策和调度可行性的影响,生产系统需要根据当前信息采取实时控制策略。文献[1]通过前瞻区间获取工件信息,以最小化工件制造期为优化目标,研究了工件组数与平行机数相同的在线分批调度问题。文献[2]建立了不相容工件组随机调度的预测模型,并以最小化工件平均生产周期为优化目标,给出了一个基于模型预测控制的在线启发式算法。文献[3]将不相容工件组的调度问题建模为G/G/C排队网络,并以最小化工件平均生产周期为优化目标,给出了相应的启发式算法。文献[4]为了实时响应模具制造过程中的机器完工和任务到达,建立了基于事件驱动的调度机制,并给出了面向准时与节能的前摄性分批算法。文献[5]针对模具制造过程中的随机性问题,建立了在制项目的交货期随机预测模型,并通过融入多模式资源受限项目调度优先规则,对在制项目进行演化。
本文根据不相容工件组在单台批处理机上分批加工的特点,以长期平均代价最小为优化目标,建立了基于半马尔可夫决策过程的系统模型;然后在模型的基础上,通过策略迭代算法分析了缓冲库容量对系统性能的影响。最后,通过基于模拟退火的Q学习算法(Q-learning algorithm combined with a simulated annealing,SA-Q)对具有大状态空间的分批调度问题进行了优化控制,仿真实验结果验证了所提算法的有效性。
1 模型的建立
假设m组不相容工件按相互独立的泊松过程随机到达,待加工工件存放在容量有限的缓冲区中,且所有工件尺寸为单位大小。属于相同组的工件能被安排在同一批中加工,加工过程不允许中断。批的加工时间和批中工件数无关,由工件组的类型决定。不考虑批的切换时间和准备时间,且批处理机容量有限。
由于工件动态到达时,非满批次的最优开启时刻为工件的到达时刻[6],则本文选取批处理机空闲时下一个工件的到达时刻和批处理机加工时批的完工时刻为决策时刻。在决策时刻,批处理机选择等待未来工件到达,还是选择一批相同组中工件进行加工是重要的决策问题。在采取加工行动时,以尽可能满的方式构成批;采取等待行动时,只等待一个工件到达。
根据决策机制的特点,建立基于半马尔可夫控制过程的系统模型。系统中用到的参数和变量定义如下:
j:工件组的类型索引,j=1,2,…,m。
C:批处理机容量。
B:缓冲库容量,m类缓冲库的容量相同。
bj:缓冲库j中工件数,表示缓冲库j的状态,且
λj:工件组j的工件到达率,工件按泊松过程到达。
vj:加工工件组j中工件的行动;另外,用v0表示等待行动。
wj:工件组j的权重,表示单位时间缓冲库j中存储一个工件的代价。
klose:流失一个工件的代价,不相容工件组中工件的流失代价相同。
Fj(t):工件组j中工件的加工时间分布,均值为1/μj。
hj:采取加工行动vj时,加载到批处理机中属于工件组j的工件数,hj=min(C,bj)。
系统工作过程中,根据实时状态进行决策。除了特殊状态下需要采取特殊的行动外,其他状态下的行动属于有限行动空间D。系统的两种特殊状态分别为:1)缓冲库都为空。系统采取等待行动直到有工件到达;2)存在缓冲库满。若批处理机空闲,则立即采取加工行动,否则等待当前加工完成再做决策;有多个缓冲库满时,则选择大的批次进行加工。
证明:1)若缓冲库中没有工件,批处理机空闲等待是合理的。2)存在一个缓冲库满时,为了避免工件流失,应优先加工已满缓冲库中的工件;多个缓冲库满时,根据加权最短加工时间优先(weighted shortest processing time first同,WSPT)规则,应优先加工值大的批次。由于不同工件组中工件尺寸相同,则选择大的满批次进行加工是合理的。
前述问题的状态变化过程可以表示为连续时间的随机过程Xt(t≥0),且{X0,X1,…,Xl…}是一个嵌入的马氏链[7]。在决策时刻Tl,系统状态可表示为Xl(令Xl=s,采取的行动可表示为系统在决策时刻Tl的状态为Xl,采取行动转移到下一状态Xl+1,并立即进入下一个决策时刻。
下面详细介绍半马尔科夫决策过程模型的建立。首先,定义系统在策略V下的状态逗留时间分布矩阵和嵌入链转移矩阵分别为和其中,Fss′(t,vs)和Pss′(vs)分别表示系统在状态s下采取行动vs转移到状态s'的状态逗留时间分布函数和转移概率函数。然后,由状态逗留时间分布和转移概率,可得到系统在策略V下的半马尔科夫核
本文假设不同组中工件的加工时间服从相互独立的指数分布,因此系统的状态逗留时间服从指数分布。根据决策行动的不同,系统的状态转移概率可以分为两类:采取等待行动时,由下一个到达的工件类型决定状态的转移;采取加工行动时,由于工件的到达过程相互独立,则系统状态的转移概率由各缓冲库的状态转移概率共同决定。
在状态s下采取等待行动v0,且下一个到达的工件属于j工件组的状态转移概率为:

采取加工行动vj时,令缓冲库j由状态bj转移到b'j的概率为当前决策过程中,其他m-1类缓冲库中工件没有被加工,令其中缓冲库i由状态bi转移到b'i的概率为由各缓冲库的状态转移概率之积,可得到系统在状态s下采取加工行动vj转移到s'的转移概率为:

系统在状态s下采取等待行动v0转移到下一状态s'过程中,系统单位时间的平均代价为:

采取加工行动时,根据系统转移到状态s'时,缓冲库j的状态b'j是否为满,可以分别计算各工件组的单位时间平均代价。当b′j≠B时,没有工件流失,则转移过程中缓冲库j中的平均工件数为当b′j=B时,缓冲库j的下一状态为满,可能产生工件流失。在缓冲库的下一状态为满时,令到达的j组工件数其中个工件卸载到缓冲库j中,其余工件流失。因此,系统在状态s下采取加工行动vj转移到下一状态s'过程中,单位时间平均代价可表示为:



2 优化算法
在前述半马尔科夫决策过程模型的基础上,可通过策略迭代方法对本文问题进行优化控制。一次迭代过程可以简单的描述为:在当前策略Vk,可通过泊松方程计算性能势向量并通过方程进行策略更新[7,8]。由于策略迭代的每一步迭代都需要计算稳态分布和泊松方程,当状态空间较大时将耗费大量计算时间和存储空间。为了有效缓解系统大状态空间导致的维数灾问题,本文通过SA-Q来寻找次优行动控制策略。
Q学习算法是强化学习中应用最广泛的学习算法之一,是一种模型无关(Model-free)的非监督学习方法;其通过仿真或观测系统的运行,不断学习并逼近状态-行动对的函数值而对问题进行求解,在不需要环境模型的情况下可以有效评估可用行动的期望效用。
前述数学模型为SA-Q提供了理论基础。根据样本转移过程,给出平均准则下的差分公式和Q值更新公式:

根据式、和样本转移可知,系统在状态s下采取等待行动和加工行动转移到下一状态s'过程中的累积代价分别如下:

为了平衡Q学习的探索和利用,避免算法进入局部最优,使用模拟退火的Metropolis接受准则设置Q学习的探索率。学习过程中每N步,由Q值表生成当前的贪婪策略,并评估当前贪婪策略的优化性能。SA-Q流程如图1所示,其中,Z为算法截止步数,ζ是模拟退火的温度衰减因子。
3 仿真结果分析
小于等于1;当TI>1时,即使批处理机一直处在满批次加工,系统中工件也会不断积累[10]。在前述数学模型的基础上,首先通过策略迭代算法分析不同缓冲库容量和流失代价对系统优化性能的影响。然后比较两组工件时,SA-Q和策略迭代算法的优化效果。本文所有仿真实验均在Microsoft Windows7(CPU 3.40GHz,RAM 7.90GB)环境下,使用MATLAB R2016a平台编程实现。
不同流失代价下两组工件的实例设置如表1所示。

表1 不同流失代价下两组工件的实例设置

图1 SA-Q流程图
不同流失代价下两组工件的最优平均代价曲线如图2所示。当klose=0时,随缓冲库容量的增大,工件的流失量减小,同时系统中平均持有的工件数增多,则最优平均代价逐渐增大。klose≠0时,工件的流失量减小,流失代价对平均代价的贡献减小,则最优平均代价随缓冲库容量的增大而衰减;且流失代价越大,流失代价对平均代价的贡献减小的越快,则曲线衰减的越快。
不同流失代价下两组工件的平均处理率曲线如图3所示。不同流失代价下平均处理率曲线随缓冲库容量的增大而增大。在相同缓冲库容量下,流失代价klose为0时工件平均处理率最小,主要原因是考虑流失代价时系统单位时间加工的工件数增大。流失代价klose为500和1000时,处理率曲线基本重合,主要原因是在缓冲库容量较小时,由于缓冲库中工件存储量的制约,工件平均处理率不会随流失代价klose的增大而增大,此时相同缓冲库容量下的工件流失率基本相同,并且流失代价越大则最优平均代价越大(如图2所示);在缓冲库容量较大时,由于工件总到达率的制约,工件平均处理率不会随流失代价klose的增大而增大。此外,不同流失代价下的平均处理率随缓冲库容量的增大趋于相同,主要原因是缓冲库容量增大,则工件的流失量减小;当工件平均处理率等于工件的到达率时,流失代价对平均代价的贡献为零。

图2 不同流失代价时的最优平均代价曲线
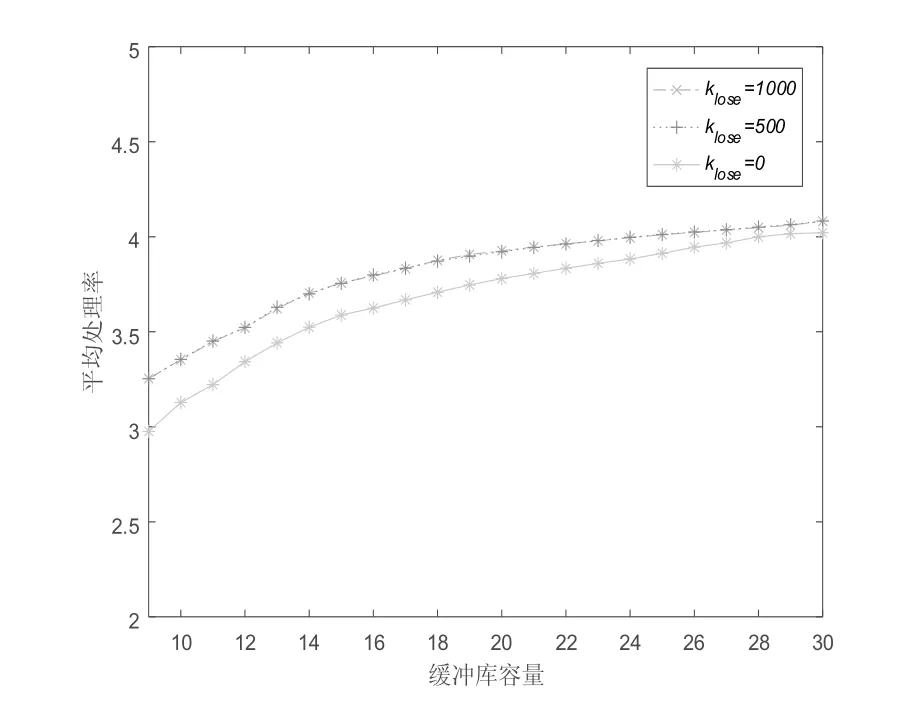
图3 不同流失代价时的平均处理率曲线
图2 和图3的实验结果表明随着缓冲库容量的增加,工件的流失率逐渐减小;且当缓冲库容量B=30时,工件组1和工件组2的平均处理率分别为3.09和1.08,近似等于两组工件的到达率。对于表1的实验数据选取缓冲库容量略大于30较合适;这样不仅可以减少库存浪费和工件流失,同时也可以保证合适的状态空间大小。
在本文不相容工件组的半马尔科夫决策过程模型中,系统状态空间((B+1)m)随工件组数的增大呈指数增大。当工件组数较大时,通过SA-Q对系统进行优化控制。下面通过实验比较工件组数为2时两种算法的性能。根据表1的实验数据,表2中选取缓冲库容量为30,流失代价klose=500,批处理机容量C=6,TI=0.7。当TI减小时,相同批处理机容量和工件处理率计算得到的工件到达率减小,则系统的缓冲库容量选为30能满足优化的需要。

表2 两组工件的实例设置和实验结果
两组工件的实例设置和实验结果如表2所列。表中列出了三种到达率比值,两种权重和两种处理率;不同组工件到达率的实际值由TI和工件处理率计算得到。
两组工件的实验结果如表2所示。表中GAP=(SA-Q/PI)-1用于表示SA-Q次优解与策略迭代最优解的相对差距。表2中SA-Q获得的次优解与最优解的相对差距总体在3%以内,实验结果说明SA-Q具有较好的优化效果。表中,1~6组的实验结果明显大于7~12组,主要原因是由于工件组1的权重增大,则其平均代价增大。此外,1~6组实验结果随到达率比值的减小而减小,主要原因是工件到达率比值减小,由TI计算得到的工件组1到达率减小,工件组2到达率增大;在前6组实验数据中,工件组1的权重大,因此平均代价随到达率比值减小而增大。在7~12组实验参数中,平均代价随到达率比值的减小由微小增大,主要原因是由TI计算得到的工件总到达率随到达率比值的减小有小幅增加,则平均代价有小幅增大。
在表2的实验数据下,系统的状态空间为961,且SA-Q在学习50万步后基本收敛到最优解,且耗时在200秒以内;其与策略迭代算法的耗时相比没有太大的优势,但当工件组数大于2时,系统状态空间呈指数增大,策略迭代算法的耗时将大幅增加,下面通过设置三组工件和四组工件的实验来说明SA-Q的优化效果。
三组工件的实例设置和实验结果如表3所示。表中列出了四组到达率比值,工件到达率的实际值由TI和工件处理率计算;根据前述实验结果,表3中选取缓冲库容量为15,流失代价klose=500,批处理机容量C=3,TI=0.4,并且只给出了工件具有相同等待代价权重的实验结果。
三组工件的实验结果如表3所示。表中,SA-Q次优解与最优解的相对差距在1%以内。三工件组实验参数中TI较小,系统的平均处理率远大于工件的到达率,则平均代价较小。

表3 三工件组的实例设置和性能比较
在表3的实验数据下,系统的状态空间为4096;SA-Q在学习1000万步后基本收敛到最优解,且计算耗时在一个小时内,相同问题策略迭代的耗时需要按天计算。在不相容工件组的分批调度问题中,缓冲库容量需要大于批处理机的容量;当工件组数大于3时,策略迭代算法将无法计算这种具有大规模状态空间的问题。
下面给出工件组数为4的SA-Q优化实验。根据前述实验结果,令B=15,C=3,klose=500,工件等待代价权重(w1,w2,w3,w4)=(1.5,1.3,1.2,1.0);并由工件处理率(μ1,μ2,μ3,μ4)=(0.5,0.6,0.7,0.8)和TI(等于0.4),计算得到的工件到达率(λ1,λ2,λ3,λ4)=(0.32,0.16,0.11,0.11)。学习过程中,每20万步由Q值表更新一次策略,并仿真评估其性能。每次评估进行20次独立实验,每次运行20万步,然后估计当前策略下系统的平均性能。
四工件组的总平均处理率曲线如图4所示,平均处理率随SA-Q学习步数的增大而增大,最终近似等于工件的总到达率,且各组工件的平均到达率分别为0.321、0.161、0.107和0.107;说明在当前缓冲库容量下系统的工件流失可以忽略不计。四工件组的平均代价优化曲线如图5所示,SA-Q学习初始曲线具有较大波动,随着学习步数的增加曲线最终收敛;说明SA-Q学到的次优策略有效减少了系统的平均代价。

图4 四组工件的总平均处理率
4 结束语
本文研究了不相容工件组在单台批处理机上的分批加工问题。首先,根据问题的特点将其建模为半马尔科夫决策过程;然后在所建模型的基础上,通过策略迭代算法分析了缓冲库容量对系统平均性能的影响;并通过比较两种算法的性能,说明了SA-Q能有效缓解大状态空间导致的维数灾问题。本文只考虑了工件加工时间为指数分布的情况,所建模型对加工时间为一般分布的问题同样适用,如爱尔兰分布等。另外,也可以扩张到相容工件组的分批加工问题。
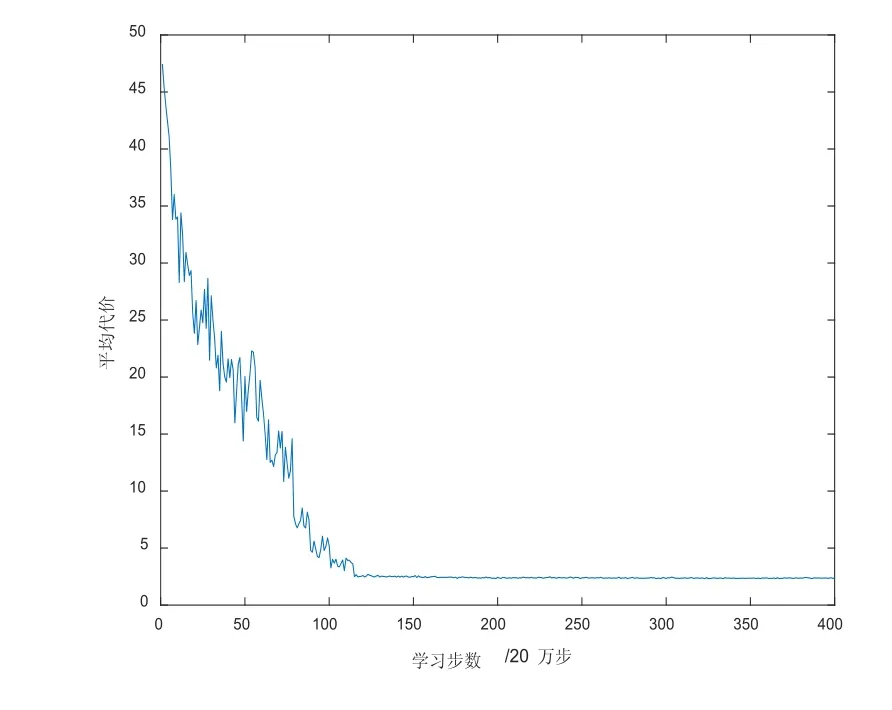
图5 四组工件的SA-Q优化曲线
[1] 李文华,柴幸,袁航,杨素芳.平行机上带有前瞻区间的不相容工件组在线排序问题[J].运筹学学报,2015,19(4):121-126.
[2] J.B.C.Tajan.Control of a Single Batch Processor with Incompatible Job Families and Future Job Arrivals[J].IEEE Transactions on Semiconductor Manufacturing,2011,24(2):208-222.
[3] J. W. Fowler.Optimal batching in a wafer fabrication facility using a multiproduct G/G/c model with batch processing[J].International Journal of Production Research,2002,40(2):275-292.
[4] 刘建军,陈庆新,毛宁,朱鑫.事件驱动的并行多机模具热处理生产调度[J].计算机集成制造系统,2015,21(4):1013-1022.
[5] 王小明,陈庆新,毛宁,刘建军.随机环境下的模具项目交货期预测方法[J].计算机集成制造系统,2012,18(2):405-414.
[6] S Yao, Z Jiang,N Li.A branch and bound algorithm for minimizing total completion time on a single batch machine with incompatible job families and dynamic arrivals[J].Computers & Operations Research,2012,39(5):939-951.
[7] Xi-Ren Cao.Semi-Markov decision problems and performance sensitivity analysis[J].Automatic Control,2003,48(5):758-769.
[8] Xi-Ren Cao. Stochastic learning and optimization:A sensitivitybased approach[J].Annual Reviews in Control,2009,33(1):11-24.
[9] H Tang, Arai Tamio. Look-ahead control of conveyor-serviced production station by using potential-based online policy iteration[J].International Journal of Control,2009,82(10):1917-1928.
[10] I Duenyas,JJ Neale. Stochastic scheduling of a batch processing machine with incompatible job families[J].Annals of Operations Research,1997,70:191-220.
Stochastic scheduling of incompatible job families on a single batch machine
TAN Qi, WANG Yong-qing, DAI Fei
TP278
:A
1009-0134(2017)06-0063-06
2017-04-10
国家自然科学基金面上项目(JZ2015GJMS0418)
谭琦(1985 -),男,湖南邵阳人,讲师,博士,研究方向为生产优化及相关研究。

