OFDM系统下基于阻尼LSQR的低复杂度检测算法研究*
赵晓君,曹琲琲
OFDM系统下基于阻尼LSQR的低复杂度检测算法研究*
赵晓君1,曹琲琲2
(1.河北农业大学信息科学与技术学院,河北 保定 071001;2.西安电子科技大学通信工程学院,陕西 西安 710071)
为了解决OFDM系统随着检测符号规模的增大,检测算法(如经典的MMSE检测算法)复杂度过高的问题,采用迭代方法替代经典算法中矩阵的相乘运算。研究了阻尼LSQR迭代算法,并提出一种改进的低复杂度检测算法,即通过使用特殊预处理矩阵去处理阻尼LSQR迭代算法中的迭代矩阵,使算法迭代速度加快,从而降低了算法的复杂度。通过理论验证与算法仿真可知,改进的算法与MMSE算法相比,可在不引起明显性能损失的前提下显著降低算法复杂度。
正交频分复用 阻尼LSQR 双选信道 低复杂度检测
1 引言
OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)是一种广泛应用于高速数据传播的无线通信系统的调制技术。OFDM系统在双选信道模型下,子载波的正交性遭到破坏,导致了严重的ICI(Inter-Carrier Interference,子载波间干扰)。因此,在高多普勒频移条件下,接收端检测性能会产生不可忽略的错误平层。
针对这一问题,研究者们提出了诸多检测算法[1-6],文献[1]中提到的匹配滤波检测方法由于无法抑制ICI,因而其频域检测性能很差且算法复杂度高。文献[2]提出了基于MMSE(Minimum Mean Squared Error,最小二乘均方误差)滤波的迭代软干扰抵消算法,但是算法复杂度随着子载波个数呈指数倍增长。文献[3]提出一种应用于基扩展信道模型的LSQR(Least Squares QR Decomposition,最小二乘QR分解)迭代算法,复杂度相对于MMSE有所降低,但是模型应用具有局限性。文献[4]实质上采用的是一种基于概率的硬干扰抵消算法,因此在性能上未能超越经典的MMSE算法。
本文的贡献在于提出了一种基于阻尼LSQR算法的低复杂度检测算法,即通过使用加窗的方式用特殊预处理矩阵去处理阻尼LSQR算法中的迭代矩阵,达到减少迭代次数的效果,从而降低算法复杂度,且不带来明显的性能下降。
2 系统模型
假设OFDM系统下子载波个数为N,则频域双选信道模型如下:

H ∈▯N×N表示频域信道矩阵,分别表示频域发送信号向量与频域接收信号向量,ùω∈▯N×1表示加性高斯白噪声向量。
3 信号检测
3.1 LSQR检测算法
假设忽略公式(1)中的噪声部分,则得到常见的线性系统模型[7]:

LSQR算法可以通过迭代的方式近似求解公式(2)描述的线性问题,其本质是一种krylov子空间算法。迭代i次后,LSQR算法构成的krylov近似子空间如下:

为了降低计算复杂度,LSQR算法通常包含两步:Golub-Kahan二对角化和二对角最小二乘问题的求解。
第一步Golub-Kahan二对角化是为了将信道矩阵H转化为(i+1)×i的二对角矩阵Bi, 这样利用LSQR算法近似求解就可以转化为求如下的最小二乘问题:

二对角阵Bi可以通过对信道矩阵H进行特征值分解得到,假设U=[u1, u2, …, ui],V=[v1, v2, …, vi]均为酉矩阵,则

因此Golub-Kahan二对角化的主要步骤如下所示[8]:
(1)初始化:β1=||y||2,u1=y/β1,α1=||HHy||2,v1=HHy/α1。
(2)循环:
For i=1, 2, ... , set

End
第二步是求解二对角化最小二乘问题。由于矩阵U,V均为酉矩阵,因此公式(2)可以变为UHHVVHs=UHy,根据公式(5)可知UHHV=Bi,又由初始化知UHy=[β1, 0, 0, …, 0]T,因此有VHs=ci,从而得到:

以上分析均为基于公式(2)描述的线性模型。前面提到,为了简化运算该模型忽略了噪声部分,但是实际系统中噪声是必须考虑的因素,因此需要将公式(2)恢复为公式(1)所描述的考虑噪声的线性模型:

3.2 预处理矩阵设计
根据上文分析,LSQR算法是通过迭代的方式减小残量误差的,迭代次数过小会导致残量误差相对放大,但是考虑到复杂度因素,迭代次数也不能趋于无限。实际上,LSQR算法复杂度会随着迭代次数增加而增加,因此需要选择最优迭代次数以实现复杂度与性能的均衡。LSQR算法中的迭代矩阵HHH的特征值越聚集,算法收敛越快,即用较少的迭代次数即可达到相同最小残量误差水平[9]。因此,引入预处理矩阵的设计,采用加窗的方式,使迭代矩阵的特征值更加收敛,即处理后迭代矩阵为PHHHHP。
预处理矩阵的设计与相关系统矩阵R=HHH+σ2IN有关[10],其中参数σ的定义与3.1中的定义相同。构造预处理矩阵如下:

其中,主对角线上元素的参数{γk}(k=0, 1, …, N-1)表示相关系统矩阵R降序排列的特征值,qk表示与第k个特征值γk对应的特征向量。传统预处理矩阵通常取值为,但经过这种方法处理后迭代矩阵的特征值会集中于一点,对于存在模型误差的系统容易引起有效信号子空间与噪声信号子空间的完全混淆。因此,本文采用文献[10]提出的修正预处理矩阵,即取值,其中ρ≥0表示修正参数,取值为ρ=trace(R)/(2N)时性能最佳[9]。采用修正预处理矩阵构造方法可以只实现与有效信号子空间有关最大特征值的收敛,从而有效避免了上述传统预处理矩阵构造方法造成的混淆问题。
3.3 改进的阻尼LSQR算法
根据上文分析,在阻尼LSQR算法中迭代矩阵变为:

用3.2节中提到的预处理矩阵设计方法处理公式(9)所示的迭代矩阵,则迭代i次后,改进的阻尼LSQR算法构成的近似子空间如下:阻尼LSQR算法情况下时,相关系统矩阵变为:

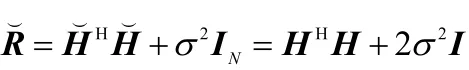
根据公式(8)可构造出用于处理阻尼LSQR算法的预处理阵P。因此,改进的算法经过i次迭代后,得到的检测信号可表示为:

其中,矩阵Γ的列向量即公式(10)所示向量集合中的元素。˘˘˘
3.4 复杂度分析
针对检测一个OFDM块所需的复乘数对算法复杂度进行分析。根据3.1节的讨论,参数αi,βi均为实数,且矩阵Bi具有二对角特性,因此算法复乘数主要体现在迭代过程中矩阵的变换部分。如表1所示,初始化过程复乘数为N2+4N,而在后面的每次迭代中需要的复乘数为4N2+8N,总复乘数为(i-1)× (4N2+8N)+(N2+4N)。因此,LSQR算法复杂度为O(iN2),而MMSE经典算法的复杂度高达O(N3)[1-2]。由于迭代次数i通常远远小于子载波个数N,因此LSQR算法复杂度明显低于MMSE算法。
4 仿真结果与分析
本文模拟的是高速移动的通信系统。设定系统工作在3.5 GHz频带,带宽为6.4 MHz,并且无线信道具有三条径,相对时延分别为:0μs、9.9 μs、17.1 μs和36.9μs。接收器速度为300 km/h,每条单径信道均为瑞利信道,循环前缀(Cyclic Prefix,CP)等于多径数减1,从而消除多径信道对系统的影响,并假设:在接收端信道信息完全已知,且已得到正确的同步。信道编码采用(7, 5)Turbo编码,交织长度为12,译码采用MAP译码。
在算法性能与复杂度评估方面,本文选择经典的MMSE算法作为参考对象,这样的选择是基于性能与复杂度两个方面的考虑。在性能方面,由于MMSE算法是基于MMSE滤波的迭代软干扰抵消算法的第一次迭代(即初始迭代),而迭代算法最终所能达到的性能由初始迭代的性能确定,因此只要初始迭代不损失性能,就能确保不降低迭代算法的最终性能。在复杂度方面,基于MMSE滤波的迭代软干扰抵消算法的复杂度集中在初始迭代,即MMSE滤波的计算。而随后的迭代可以利用逆矩阵更新来避免MMSE滤波计算的过高复杂度,因此用本文算法替代MMSE滤波即可在不引入明显性能损失的前提下显著降低迭代软干扰抵消算法的整体复杂度。
图1比较了传统的预处理矩阵设计方法、修正后的设计方法以及不加预处理矩阵三种情况下,算法迭代次数对性能影响的比较。仿真时,子载波个数为64,归一化最大多普勒频移为0.1,多径数为3,16QAM调制,接收端检测算法统一为LSQR算法。其中,图1(a)、图1(b)、图1(c)分别给出了信噪比(Signal to Noise Ratio,SNR)在20 dB、25 dB、30 dB下性能随迭代次数变化的曲线图,而图1(d)以加修正后预处理矩阵为例给出了不同信噪比下性能随迭代次数变化的曲线图。仿真曲线图表明,误比特率(Bit Error Rate,BER)呈现出凸函数特性,即存在最佳迭代次数。例如,根据图1(a)、图1(b)可知,加修正后预处理矩阵时,最小BER落在了迭代8次处,图1(c)中最佳迭代次数是12,然而根据图1(d)所示,三种信噪比情况下迭代次数在8至14范围内,性能趋于平稳并不会产生急剧变化。因此为了降低复杂度,选择8作为加修正预处理矩阵情况的最佳迭代次数。同理可知在不加预处理矩阵的情况下,在迭代14次时性能最佳。传统的预处理矩阵设计方法随着迭代次数的增加性能反而下降,甚至在相同迭代次数下性能比未加预处理矩阵的方法还要差,这印证了上文分析:传统预处理矩阵设计方法混叠了有效信号子空间与噪声信号子空间,存在缺陷。

图1 迭代次数对误比特性能的影响

表1 LSQR算法复杂度分析
图2给出了最佳迭代次数下经过修正预处理矩阵处理后的阻尼LSQR算法,即本文提出的算法的BER性能。与最佳迭代次数下不加任何预处理矩阵处理的阻尼LSQR算法相比,提出的算法在性能上提升了约5 dB。而与经典的MMSE算法相比,性能接近,甚至在高SNR下性能优于MMSE。因此,本文提出的算法可以实现复杂度降低而不引起明显的性能损失。

图2 改进的阻尼LSQR算法性能曲线仿真图
5 结束语
针对高速移动的通信系统,本文提出一种低复杂度检测算法:用修正预处理矩阵对阻尼LSQR迭代算法的迭代矩阵进行加窗处理,从而加快收敛速度。选择MMSE算法作为参考对象,这是因为MMSE是并行迭代软干扰抵消的基础(第1次迭代),而迭代算法的最终性能是由初始算法的性能决定的。仿真结果表明,本文所提方法与经典MMSE检测算法相比,能实现算法复杂度与性能的折衷。
[1] YANG-SEOK C, VOLTZ P J, CASSARA F A. On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels[J]. IEEE Transactions on Communications, 2001,49(8): 1375-1387.
[2] SCHNITER P. Low-complexity equalization of OFDM in doubly selective channels[J]. IEEE Transactions on Signal Processing, 2004,52(4): 1002-1011.
[3] HRYCAK T, DAS S, MATZ G, et al. Low Complexity Equalization for Doubly Selective Channels Modeled by a Basis Expansion[J]. IEEE Transactions on Signal Processing, 2010,58(11): 5706-5719.
[4] A SEPTIMUS Y K, AND I BERGEL. A Spectral Approuach to Inter-Carrier Interference mitigation in OFDM Systems[J]. IEEE Transactions on Communications, 2014,62(8): 2802-2811.
[5] 王薇,殷勤业,穆鹏程. 高移动环境下利用无线信号空域特征实现OFDM系统的ICI消除[J]. 通信学报, 2015(8):76-82.
[6] 韩华,吴乐南. 基于LSQR算法和加窗技术的判决反馈均衡器[J]. 电路与系统学报, 2010(6): 117-121.
[7] Paige, Christopher C, Saunders, et al. LSQR: An algorithm for sparse linear equations and sparse least square problems[J]. ACM Trans. Math. Software, 1982(1): 43-71.
[8] G Golub, C F Van Loan. Matrix Computations[M]. 3rd. Baltimore: The Johns Hopkins University Press, 1996.
[9] TONG J, SCHREIER P J, WELLER S R. Design and Analysis of Large MIMO Systems With Krylov Subspace Receivers[J]. IEEE Transactions on Signal Processing, 2012,60(5): 2482-2493.
[10] JUN T, SCHREIER P J. Regularized Preconditioning for Krylov Subspace Equalization of OFDM Systems over Doubly Selective Channels[J]. IEEE Wireless Communications Letters, 2013,2(4): 367-370.★

赵晓君:助教,硕士毕业于西安电子科技大学,现任职于河北农业大学信息科学与技术学院,主要从事通信信号处理与信号检测的研究。

曹琲琲:副教授,博士毕业于西安电子科技大学,现任职于西安电子科技大学通信工程学院,主要从事无线通信信号检测与处理方面的研究工作。
Research on Low-Complexity Detection Algorithm Based on Damped LSQR in OFDM System
ZHAO Xiaojun, CAO Feifei
(1. College of Information Science and Technology of Hebei Agricultural University, Baoding 071001, China; 2. School of Telecommunications Engineering of Xidian University, Xi'an 710071, China)
With the increased scale of the detected symbol in OFDM system, the detection algorithm such as the classic MMSE algorithm suffers from the very high complexity. In order to overcome the drawback, the iterative method is used to replace the matrix multiplication operation in the classic algorithm. The LSQR iterative algorithm was studied and an improved low-complexity detection algorithm was proposed, in which the specifically preprocessed matrix is used to handle the iterative matrix in the damped LSQR iterative algorithm to accelerate the iterative speed and reduce the algorithm complexity. Both the theoretical proof and the simulation results demonstrate that the proposed algorithm can highly reduce the algorithm complexity in the premise of less performance loss compared with MMSE algorithm.
OFDM damped LSQR doubly selective channel low-complexity detection
10.3969/j.issn.1006-1010.2017.16.015
TN919
A
1006-1010(2017)16-0075-06
赵晓君,曹琲琲. OFDM系统下基于阻尼LSQR的低复杂度检测算法研究[J]. 移动通信, 2017,41(16): 75-80.
国家自然科学基金项目(61102058)
2017-05-25
责任编辑:刘妙 liumiao@mbcom.cn

