概率解题错误分析

☉湖北省武汉中学 田 靖

概率解题错误分析

☉湖北省武汉中学 田 靖

在概率解题过程中常常陷入一些误区，让人觉察不到自己的错误.其原因是因为没有真正理解概率的模型，以及事件的度量，从而导致了错误思维的发生.本文以如下几道高考模拟题为例进行分析.

例1在某校教师趣味投篮比赛中，比赛规则是：每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖.已知教师甲投进每个球的概率都是

（1）记教师甲在每场的6次投球中投进球的个数为x，求x的分布列及数学期望；

（2）求教师甲在一场比赛中获奖的概率.

解析：（1）由题意可得x的所有可能取值为0，1，2，3，4，5，6.

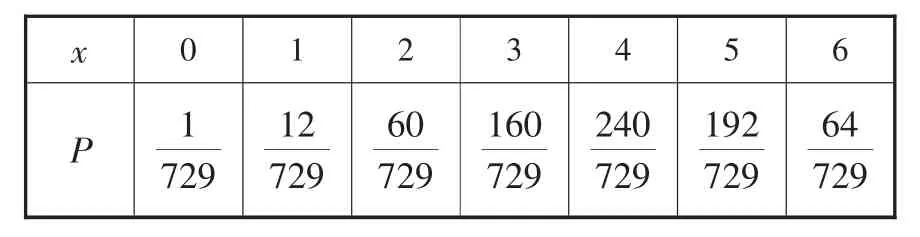
（2）设教师甲在一场比赛中获奖为事件A，包含恰好投进4个球，恰好投进5个球，恰好投进6个球共三种情况，故P（A）=，所以教师甲在一场比赛中获奖的概率为

这道题能得到这样的解法其实是一件很自然的事情，但是有时多思考一会，觉得第一问如果换一种分析方式是不是也正确呢？

投球事件的结果只能有这7种可能，分别投进0个球，1个球，2个球，3个球，…，6个球.所以有：

出现这样截然不同的结果，原因在于求概率时将概率模型误当成了古典概型.例如：“第一个球投进，后五个球投不进”这个事件的概率与“第一个球投进，后五个球也都投进”这个事件的概率是不等的.

例2设袋中有4只白球和2只黑球，现从袋中无放回地摸出2只球.

（1）求这2只球都是白球的概率；

（2）求这2只球中1只是白球，1只是黑球的概率.

解析：我们把4只白球分别标为1，2，3，4号，2只黑球标为5，6号.则基本事件有：（1，2），（1，3），…，（1，6），（2，1），（2，3），…，（2，6），…，（6，1），（6，2），…，（6，5），共30个.

（1）用A表示“2只球都是白球”这一事件，则A=｛（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）｝，共12个.

（2）用B表示“2只球中1只是白球1只是黑球”这一事件，则B=｛（1，5），（1，6），（2，5），（2，6），（3，5），（3，6），（4，5），（4，6），（5，1），（5，2），（5，3），（5，4），（6，1），（6，2），（6，3），（6，4）｝，共16个.

错解：一次摸出2只球，观察结果只能是（白，白），（白，黑），（黑，黑）3种情况.

（1）用A表示“2只球都是白球”这一事件，则A=｛（白，白）｝，所以P（A）=

（2）用B表示“2只球中1只是白球1只是黑球”这一事件，则B=｛（白，黑）｝，所以P（B）=

出现这个错误的原因是：（白，白），（白，黑），（黑，黑）3种结果的出现不是等可能的.

例3在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一射线CM，与线段AB交于点M，求AM＜AC的概率.

错解：如图1，点M随机地落在线段AB上，故线段AB的长为基本事件的度量.

当M位于线段AD（不含端点AC=AD）上时，AM＜AD，所以线段AD的长为所求事件的度量.

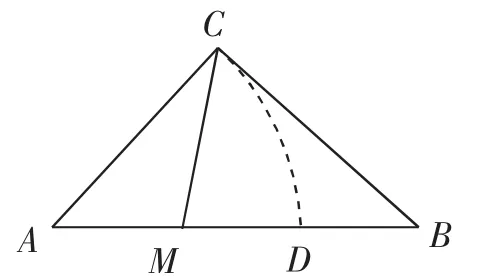
图1

出现这个错误的原因是：本题是在∠ACB内作射线CM，等可能分布的是CM在∠ACB内的任一位置，因此基本事件的度量应是∠ACB的大小，而不是线段AB的长.

正解：AM＜AC的概率应该为满足条件的∠ACM与∠ACB大小的比，即P（AM＜AC）=

变式：已知等腰Rt△ACB，在斜边AB上任取一点M，求AM的长小于AC的长的概率.

解析：因为M点可以等可能地取遍线段AB上的点，所以P（AM＜AC）=

概率是高考考查的热点问题，如果对概率知识理解不够透彻就往往会陷入困境.所以，在解答概率问题时，需要认清概率模型，找到事件正确的度量，对号入座，才能给出正确的答案.