熵损失函数下Burr(α)X分布参数的贝叶斯估计

陈家清，王 玉，陈志强

（武汉理工大学 理学院，武汉 430070）

熵损失函数下Burr(α)X分布参数的贝叶斯估计

陈家清，王 玉，陈志强

（武汉理工大学 理学院，武汉 430070）

文章研究了Burr(α)X分布参数的各类贝叶斯估计问题。在熵损失函数下分别获得了参数的贝叶斯估计、经验贝叶斯估计、多层贝叶斯估计和E-Bayes估计。证明了参数经验贝叶斯估计的渐近最优性，讨论了参数多层贝叶斯估计和E-Bayes估计的稳健性，通过蒙特卡洛方法对各类估计的MSE进行了数值模拟和比较分析，结果表明：经验贝叶斯估计的均方误差最小，精度较高。

Burr X分布；Bayes估计；经验Bayes估计；多层Bayes估计；E-Bayes估计

0 引言

1942年，Burr在研究寿命数据模型时给出了12类分布函数族[1]，其中Burr X分布是在生存分析问题中使用较广的重要分布之一。Raqab和Kundu[2]指出Burr X分布在处理常规的寿命数据和强度数据时效果非常显著，并且Burr X分布与weibull分布、Gamma分布和某些广义指数分布一样，具有很好的处理生存数据问题的统计性质，并且它对截尾数据的统计分析方面较其他寿命分布会更加方便。因此，近年Burr X分布受到许多学者的广泛关注。

Burr(α)X分布函数及其概率密度函数分别如下：

本文基于熵损失函数研究了Burr(α)X分布参数α的各类贝叶斯估计。通过熵损失函数分别获得了参数的贝叶斯估计、经验贝叶斯估计、多层贝叶斯估计以及E—Bayes估计。进一步证明了所构造的经验贝叶斯估计是渐近最优的，同时讨论了多层贝叶斯估计和E—Bayes估计的稳健性。最后，利用蒙特卡洛方法对各类估计的均方误差（MSE）进行了数值模拟，并对估计的优良性进行了比较分析。

1 贝叶斯估计和经验贝叶斯估计

1．1 一致最小方差无偏估计(UMVUE)

假设x1,x2,...,xn为来自Burr(α)X分布的一组样本，其联合密度为：

易知Burr(α)X分布来自指数分布族，并且为α的充分完备统计量。

引理1[3]：设T为充分完备统计量， (T)为g(θ)的一个无偏估计，满足 Var((T))＜∞ ，对任意θ∈Θ ，则(T)是g(θ)的UMVUE，且在几乎处处意义下，该估计是唯一的。

定理1：对于Burr(α)X分布，其未知参数α的一致最小方差无偏估计为，且在几乎处处意义下，该估计还是唯一的。

1．2 贝叶斯估计

本文取参数α的先验分布为共轭先验分布Gamma(β,λ),即 π(α)=Gamma(β,λ)，由式（3）及贝叶斯公式可得α的后验分布密度函数为：

即 π(α|x1,x2,...,xn)=Gamma(n+β,λ+T(x))

定义1[4]：设随机变量X具有概率密度函数f(x,α)，其中α为参数，若δ是α的一个估计，则熵损失函数定义为似然比对数的数学期望，即：

引理2：在熵损失函数（5）下，对于任意的先验分布π(α)，α的贝叶斯估计为，且该贝叶斯估计具有唯一性。

证明：设δ(x)为α的贝叶斯估计，其中x=(x1,x2,...,xn)，则在熵损失函数下，α的贝叶斯风险为：

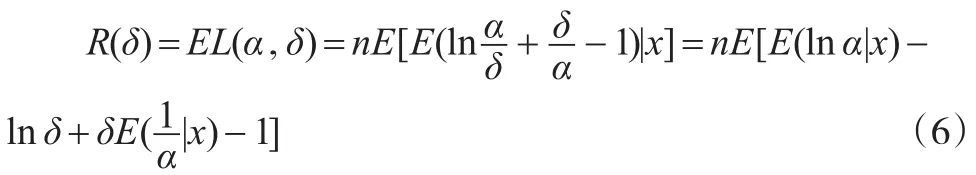
要使R(δ)达到最小，只需使最小，令得时，R(δ)有极小值，所以为α的贝叶斯估计，又易知g(t)是关于t的严格凸函数，所以δ是其唯一的极小值点，即δ是其唯一的贝叶斯估计。

定理2：在熵损失函数（5）下，取Burr(α)X分布参数α的先验分布为Gamma(β,λ)，则参数的贝叶斯估计为，且该估计是唯一的。

证明：由引理2知，在熵损失函数（5）下α的唯一贝叶斯估计为

1．3 经验贝叶斯估计

Robbins[5]和Efron&Morries[6]分别在1955年和1972年提出了两种不同的经验贝叶斯方法。前者一般称为非参数经验贝叶斯(NPEB)方法，该方法主要是利用非参数方法来进行贝叶斯估计，对先验分布的信息需求不多；后者称为参数经验贝叶斯(PEB)方法，该方法首先是利用历史样本数据来估计先验分布中的参数，然后再对样本分布中的参数进行贝叶斯估计，因此需要知道先验分布的分布类型，并且要有一些历史数据。本文将采用后者的PEB方法对Burr X分布的参数进行估计。

设有X1,X2,...,Xk为k个历史样本，其中Xi=(xi1,xi2,...,xin)。又由可得统计量T的k个历史样本，设为t1,t2,...,tk，由T～Γ(n,α)及α的先验分布π(α)可以得到T的边缘分布为：

下面将利用矩估计的方法来估计先验分布中的参数β和λ。由式（8）可得T的一阶矩和二阶矩分别为：

且其方差为：

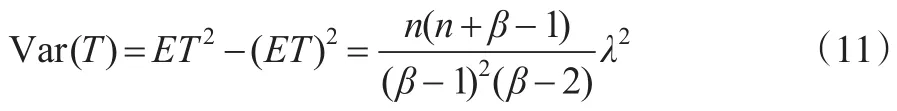
从而利用历史样本可以求得T的样本均值和样本方差，再由矩估计方法可以得到：

定义2[7]：如果对任何先验分布有就叫做渐近最优的经验贝叶斯估计。其中Rk是经验Bayes估计的全面Bayes风险，是Bayes估计的贝叶斯风险。

定理3：在熵损失函数和伽玛共轭先验分布下，当ns2-＞0 时，Burr X分布参数α的经验贝叶斯估计是渐近最优的经验贝叶斯估计。

证明：当k→∞时，由大数定律可得：

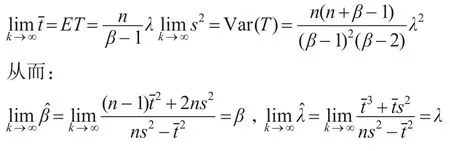
所以：

即当k→∞时，经验贝叶斯估计是收敛于贝叶斯估计的。又由：

其中：

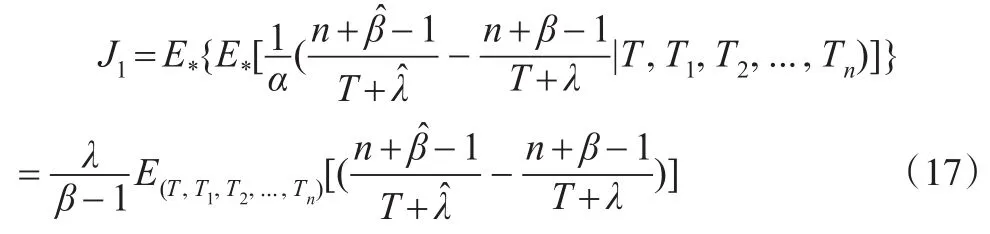
此处E*表示在ns2-＞＞0 的条件下对 (T,α),T1,T2,...,Tn的联合分布求期望。由又由ns2-＞ ＞ 0 ，可得于是：

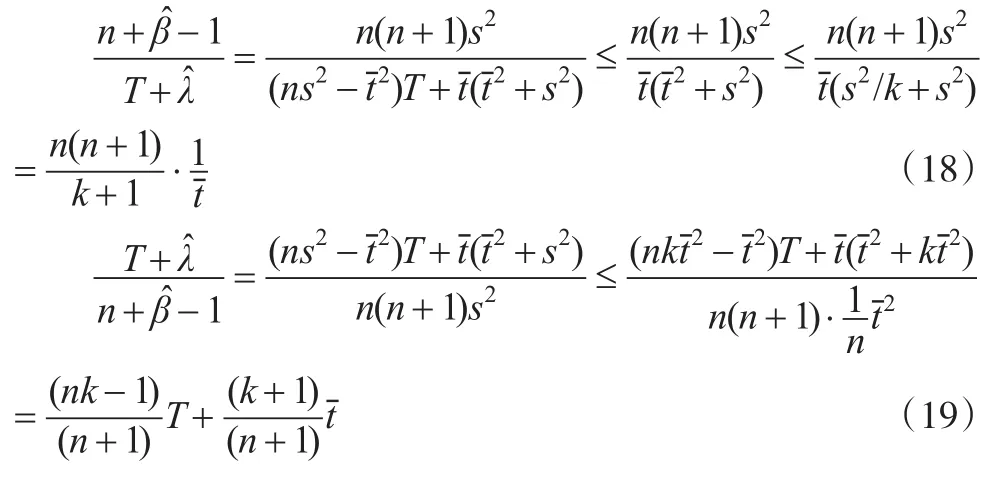
因此由式（18）和式（19）可得：

由于T,T1,T2,...,Tn相互独立且服从参数相同的Gamma分布，易知E*(1/)＜ ∞ ，E*()＜ ∞ ，E*(1/T)＜ ∞ ，从而有：

再结合式（20）和式（21）知J1和J2都满足控制收敛定理的条件，于是：

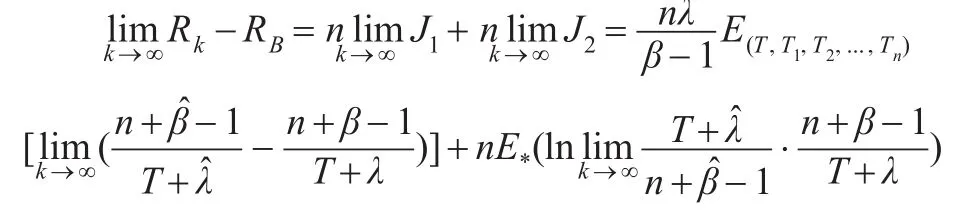
2 多层Bayes估计和E-Bayes估计

2．1 多层Bayes估计

Good[8]在1956年首次提出了多层Bayes估计方法，并证明了所获得的Bayes估计具有较好的稳健性。事实上多层Bayes估计是一种构造先验分布的方法，该方法主要是通过构造参数的多层先验分布，进而得到了参数Bayes估计。

定义3[8]：设随机变量X有密度函数f(x,λ)，参数λ的先验分布为π(λ|a,b)，超参数服从密度函数为π(a,b)的分布，则λ的多层先验密度为λ的多层后验密度为，则在损失函数LE(λ,δ)下，以 π(λ)为先验分布的λ的贝叶斯估计称为λ的多层贝叶斯估计。

由文献[9]知，若根据先验信息知道产品的失效率小的可能性大，或者失效率大的可能性小，此时应选取β和λ使得 π(α|β,λ)为α的减函数。由及α＞0,β＞0,λ＞0，可得当0＜β＜1且λ＞0时＜0 ，即 π(α|β,λ)为α的减函数。进一步考虑到Bayes估计的稳健性，此时所选取的λ不宜过大，应有一个界限，不失一般性，设c为λ的上限（c＞0为常数且c应较小）。因此，本文选取超参数β和λ的先验分布分别为U(0,1)和U(0,c)，于是得到如下定理4的结果。

定理4：在熵损失函数（5）下，取Burr(α)X分布参数α的先验分布为Gamma(β,λ)，其中超参数β和λ的先验分布分别选取为 π1(β)=U(0,1)，π2(λ)=U(0,c)，则Burr X参数α的多层贝叶斯估计为：

证明：由超参数β和λ的先验分布分别为 π1(β)=U(0,1)，π2(λ)=U(0,c)，因此超参数β和λ的联合密度为于是由定义3得参数α的多层先验分布为dλdβ从而参数α的多层后验密度为：

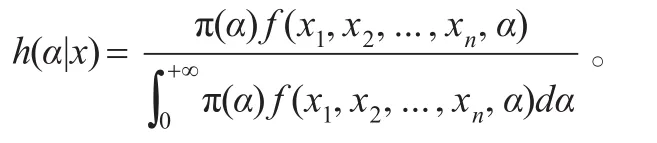
因此，在熵损失函数(5)下参数的多层贝叶斯估计为：

由式（23）可以看出，多层贝叶斯估计往往是利用如上的两个积分的比率来表示，在实际应用中多需要利用数值方法来计算。

2．2 E-Bayes估计

由于多层贝叶斯估计经常涉及到高维积分的计算，这在一定程度上制约了多层Bayes方法的应用，为了解决这一问题，韩明[10]提出了一种新的贝叶斯估计方法，即E-Bayes估计,并证明了对于某些分布，E-Bayes估计是收敛到多层贝叶斯估计的。

定义4：[10]设随机变量X服从密度函数为f(x,λ)的分布，λ的先验分布为π(λ|a,b)，其中(a,b)∈D称为超参数，(a,b)的分布为 π(a,b)。如果(a,b)是在损失函数LE(λ,δ) 及 先 验 分 布 π(λ|a,b) 下 的 Bayes 估 计 ，则 称为λ的 E-Bayes 估 计 ，其 中(a,b)是连续的且满足

定理5：在熵损失函数（5）下，选取Burr X参数α的先验分布为Gamma(β,λ)，且选取超参数β和λ先验分布分别 取 为 π1(β)=U(0,1)，π2(λ)=U(0,c)，则 参 数α的E-Bayes估计为，且该估计还是唯一的。

证明：由定理2可知α的唯一贝叶斯估计为由E-Bayes估计的定义可得：

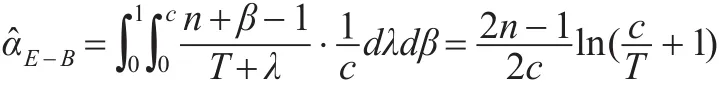
3 数值模拟

首先，通过蒙特卡洛方法对经验贝叶斯估计的渐近最优性进行了验证，然后在c取不同值的情形下，对多层贝叶斯估计和E-Bayes估计的稳健性进行了模拟分析，最后在不同的样本量下，对经验贝叶斯估计、一致最小方差无偏估计、多层贝叶斯估计和E-Bayes估计的均方误差（MSE）进行了比较分析。

（1）经验贝叶斯估计渐近最优性模拟。由定理3可知，当k→∞时，参数α经验贝叶斯估计收敛于贝叶斯估计，且在ns2-＞＞0 的条件下，经验贝叶斯估计的风险是收敛到贝叶斯估计的风险的，下面利用蒙特卡洛方法来验证这一结论。

图1 和 随 k 的变化

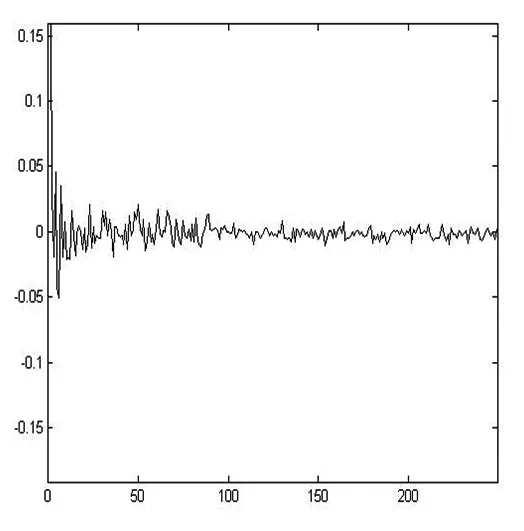
图2 - 随 k 变化

从图1和图2可以看出，随着历史数据的个数k的增加，经验贝叶斯估计确实会收敛到贝叶斯估计，并且在k＞100后，该收敛过程达到稳定。

图3 Rk-随k的变化

从图3中可以看出，随着k的增大，Rk-→0，从而经验贝叶斯估计是渐近最优的。

（2）多层贝叶斯估计和E-Bayes估计稳健性模拟。此处通过选取不同的样本量和c值来讨论多层贝叶斯估计和E-Bayes估计的稳健性，数值模拟的结果如下页表1所示。

由表1的数值算例可以看出，对于相同的c，-B和非常接近；对于不同的c(c=2,3,4,5,6)，-B和都是比较稳健的，随着样本容量n的增加(10→20→30→60→100)，-B和越来越接近，但比-B的极差小，因此对于Burr(α)X分布而言，多层Bayes估计比E-Bayes估计的稳健性要好。

（3）各类估计MSE的比较模拟。给定α,k,c的值，运用Monte-Carlo方法产生样本容量为n且服从Gamma(n,α)（T的分布）的样本和历史样本。利用该组数据给出参数α的一致最小方差无偏估计、经验贝叶斯估计、多层贝叶斯估计和E-Bayes估计。重复上述模拟1000次，分别计算各种估计的均方误差，模拟结果如下页表2所示。

表1 多层贝叶斯估计和E-Bayes估计

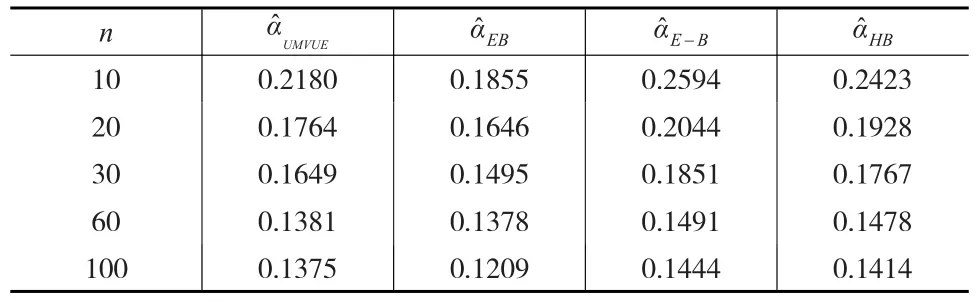
表2 各类参数估计均方误差的数值模拟(α=1.2,k=10,c=4)

从表2可以看出，当样本量n相同时，经验贝叶斯估计的均方误差最小，精度最高，其次是一致最小方差无偏估计、多层贝叶斯估计，E-Bayes估计的均方误差最大，精度最低。当样本量n增大时，各个估计的均方误差都变小，但其变化幅度开始很大，后来逐渐变小。在实际应用中，当拥有一定的历史数据时，可以利用经验贝叶斯方法，当不具备这一条件时，一致最小方差无偏估计是一个不错的选择。

4 结束语

本文给出了Burr X分布的参数α的一致最小方差无偏估计、贝叶斯估计、经验贝叶斯估计、多层贝叶斯估计和E-Bayes估计，并证明了经验贝叶斯估计的渐近最优性。还利用数值模拟对多层贝叶斯估计和E-Bayes估计的稳健性进行了比较分析，同时对各类参数估计的均方误差进行了数值模拟。结果表明多层贝叶斯估计比E-Bayes估计的稳健性好，而经验贝叶斯估计均方误差最小，估计效果最好。因此在实际工程应用中，采用经验贝叶斯方法较好。

[1]Burr I W.Cumulative Frequency Functions[J].Ann.Math.Statist.,1942,(13).

[2]Raqab M Z,Kundu D.Burr Type X Distribution:Revisited[J].JPSS,2006,(8).

[3]师义民,许勇,周丙常.近代统计方法选讲[M].西安:西北工业大学出版社,2008.

[4]鄢伟安,师义民,孙天宇,王亮.熵损失下广义指数分布的可靠性估计[J].系统工程理论与实践,2011,31(9).

[5]Robbins H.An Empirical Bayes Approach to Statistics[C].Proc.Third Berleley Symposium on Math.Statist.,1955,(1).

[6]Efron B,Morris C.Limiting the Risk of Bayes and Empirical Bayes Estimators-Part II:The Empirical Bayes Case[J].Journal of the American Statistical Association,1972,67(337).

[7]Robbins H.The Empirical Bayes Approach to Statistical Problems[J].Ann.Math.Statist.,1964,(35).

[8]Good I J.On the Estimation of Small Frequencies in Contingency Tables[J].J.Roy.Statist.Soc.B,1956,(18).

[9]韩明.多层先验分布的构造及其应用[J].运筹与管理,1997,6(3).

[10]韩明.可靠度的一种新估计方法[J].兵工学报,2004,25(1).

Bayes Estimation of Parameter for Burr(α )X Distribution under Entropy Loss Function

Chen Jiaqing,Wang Yu,Chen Zhiqiang
(College of Science,Department of Statistics,Wuhan University of Technology,Wuhan 430070,China)

This paper investigates all kinds of Bayes estimations of parameter for Burr(α)X distribution,and respectively obtains Bayes estimation,empirical Bayes estimation,hierarchical Bayes estimation and E-Bayes estimation under the entropy loss function.Furthermore the paper verifies that the empirical Bayes estimation is asymptotically optimal,and at the same time discusses the robustness of the hierarchical Bayes estimation and E-Bayes estimation.Finally the paper conducts a value simulation and comparison of the mean square error(MSE)of various estimations based on Monte Carlo method.The study result shows that the empirical Bayes estimation has minimum MSE and high-precision.

Burr X distribution;Bayes estimation;empirical Bayes estimation;hierarchical Bayes estimation;E-Bayes estimation

O212.1

A

1002-6487（2017）20-0005-05

国家自然科学基金面上资助项目（81671633）；湖北省自然科学基金资助项目（2014CFB863）

陈家清（1972—），男，湖北襄阳人，博士，副教授，研究方向：贝叶斯统计学。

(责任编辑/亦 民)