k元n方体的条件强匹配排除

冯 凯

(山西大学 计算机与信息技术学院，太原 030006)(*通信作者电子邮箱fengkai@sxu.edu.cn)

k元n方体的条件强匹配排除

冯 凯*

(山西大学 计算机与信息技术学院，太原 030006)(*通信作者电子邮箱fengkai@sxu.edu.cn)

为了度量发生故障时k元n方体对其可匹配性的保持能力，通过剖析条件故障下使得k元n方体中不存在完美匹配或几乎完美匹配所需故障集的构造，研究了条件故障下使得k元n方体不可匹配所需的最小故障数。当k≥4为偶数且n≥2时，得出了k元n方体这一容错性参数的精确值并对其所有相应的最小故障集进行了刻画；当k≥3为奇数且n≥2时，给出了该k元n方体容错性参数的一个可达下界和一个可达上界。结果表明，选取k为奇数的k元n方体作为底层互连网络拓扑设计的并行计算机系统在条件故障下对其可匹配性有良好的保持能力；进一步地，该系统在故障数不超过2n时仍是可匹配的，要使该系统不可匹配至多需要4n-3个故障元。

并行计算机系统；互连网络；k元n方体；完美匹配；条件故障

0 引言

设M是图G中的边子集且M中任意两条边无公共端点，则称M为G的一个匹配。若|G|为偶数，G中匹配M满足|M|=|G|/2，则称M为G的一个完美匹配。若|G|为奇数，G中匹配M满足|M|=(|G|-1)/2，则称M为G的一个几乎完美匹配。若图G中存在完美匹配或几乎完美匹配，则称G是可匹配的；否则称G是不可匹配的。对于图G中任意一点v，G中所有与v相邻的点构成的集合称为v的邻域，记为NG(v)；G中与点v相关联的边的数目称为v的度，记为dG(v)。若V(G)可以划分成两个非空子集X和Y，使得每条边都有一个端点在X中，另一个端点在Y中，则称G为一个二部图，(X,Y)为G的一个二分类。对于文中其他未加定义而被使用的图论术语和记号参见文献[1]。

并行计算机系统通常以某个无向简单图G=(V(G),E(G))作为其基本的互连网络，其中V(G)中每个顶点对应一个处理器，E(G)中每条边对应一对处理器之间的一条直接通信线路。对于某些特定的系统，要求其互连网络中每个处理器在任意时间都需要被指定一个与其配对的处理器，这些处理器对之间通过相互通信协同工作，整个系统才能正常运行。为了优化资源配置、降低通信延迟，人们希望这样的处理器对之间是通过直接的物理连线连接的。在此背景下，Brigham等[2]提出了互连网络的匹配排除问题，即一个互连网络中至少需要多少条边发生故障才可以使该网络是不可匹配的。在实际构建的系统中元器件和通信信道发生故障是随机的、不可预知的，互连网络中某些点和边可能同时发生故障。基于这一考虑，Park等[3]对匹配排除问题进行了推广，提出了互连网络的强匹配排除问题。设G=(V(G),E(G))是一个无向简单图，F⊆V(G)∪E(G)为G中的故障集。若GF是不可匹配的，则称F为G的一个强匹配排除集。G的含元素最少的强匹配排除集中元素的个数称为G的强匹配排除数，记为smp(G)。若G中强匹配排除集F满足|F|=smp(G)，则称F为G的一个最小强匹配排除集。近来，互连网络的强匹配排除问题得到了大量的关注[4-5]。对于带有故障诊断算法的系统，系统发生故障导致出现孤立点的可能性很小。Park等[6]于2013年对条件故障下(即假定系统不会由于发生故障而产生孤立点)互连网络的强匹配排除问题进行了研究。称图G中相应的强匹配排除集为G的条件强匹配排除集，相应的强匹配排除数记为smp1(G)。

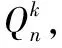
1 主要结果

由定义可知，图中一个条件强匹配排除集是一个特殊的强匹配排除集。下面的性质显然成立。

性质1 若图G中有强匹配排除集和条件强匹配排除集，则smp(G)≤smp1(G)。

性质2[6]对于图G中的一条路(u,z,v)，构造故障集Fuzv如下：

1)Fuzv包含(NG(u)∩NG(v)) {z}中的每个点；

2)若(u,v)∈E(G)，Fuzv包含边(u,v)；

3)对任意的w∈NG(u)NG(v)，Fuzv或者包含w或者包含(u,w)；

4)对任意的w∈NG(v)NG(u)，Fuzv或者包含w或者包含(v,w)。

若GFuzv不含孤立点且|GFuzv|为偶数，则Fuzv为G的一个条件强匹配排除集。

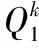
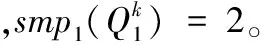
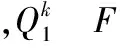
证毕。

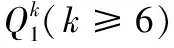
引理2[6]设G为m正则连通二部图，其中m≥3，则smp1(G)=2且G中任一个最小条件强匹配排除集均由同一部集中的两个点构成。

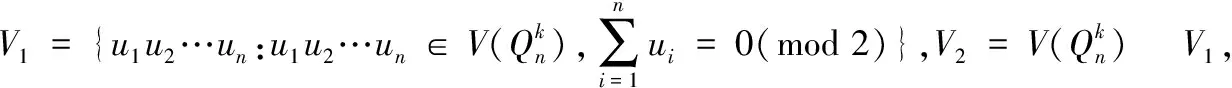
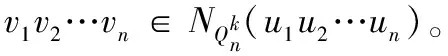
证毕。

引理3 设k≥3为整数，n≥1为整数，则有：

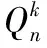
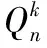
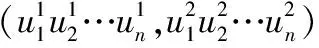
证毕。

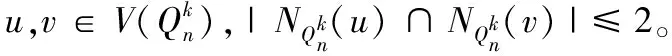
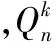
1) 存在d∈{1,2,…,n}使得ud=vd。

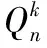
2) 对任意d∈{1,2,…,n}有ud≠vd。

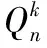
证毕。

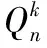
证毕。

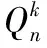
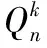
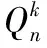
证毕。

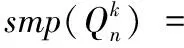
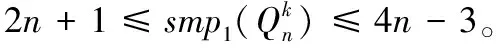
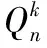
证毕。

由定理4，显然有下面的结论成立。

2 结语

References)

[1] BONDY J A, MURTY U S R. Graph Theory [M]. New York: Springer, 2008:1-450.

[2] BRIGHAM R C, HARARY F, VIOLIN E C, et al. Perfect-matching preclusion [J]. Congressus Numerantium, 2005, 174: 185-192.

[3] PARK J H, IHM I. Strong matching preclusion [J]. Theoretical Computer Science, 2011, 412(45): 6409-6419.

[4] FENG K, WANG S. Strong matching preclusion for two-dimensional torus networks [J]. International Journal of Computer Mathematics, 2015, 92(3): 473-485.

[5] CHENG E, KELM J, RENZI J. Strong matching preclusion of (n,k)-star graphs [J]. Theoretical Computer Science, 2016, 615: 91-101.

[6] PARK J H, IHM I. Strong matching preclusion under the conditional fault model [J]. Discrete Applied Mathematics, 2013, 161(7/8): 1093-1105.

[7] WANG S, WANG R, LIN S, et al. Matching preclusion fork-aryn-cubes [J]. Discrete Applied Mathematics, 2010, 158(18): 2066-2070.

[8] WANG S, FENG K, ZHANG G. Strong matching preclusion fork-aryn-cubes [J]. Discrete Applied Mathematics, 2013, 161(18): 3054-3062.

[9] 杨玉星,王世英.k元n立方网络的k圈排除问题的递归算法[J].计算机应用,2013,33(9):2401-2403.(YANG Y X, WANG S Y. Recursive algorithm fork-cycle preclusion problem ink-aryn-cubes [J]. Journal of Computer Applications, 2013, 33(9): 2401-2403.)[10] YANG Y, LI J, WANG S. Embedding various cycles with prescribed paths intok-aryn-cubes [J]. Discrete Applied Mathematics, 2017, 220: 161-169.

[11] PETERSON C, SUTTON J, WILEY P. iWarp: a 100-MOPS, LIW microprocessor for multicomputers [J]. IEEE Micro, 1991, 11(3): 26-29.

[12] ANDERSON E, BROOKS J, GRASSL C, et al. Performance of the CRAY T3E multiprocessor [C]// Proceedings of the 1997 ACM/IEEE Conference on Supercomputing. New York: ACM, 1997: 1-17.

[13] ADIGA N R, BLUMRICH M A, CHEN D, et al. Blue Gene/L torus interconnection network [J]. IBM Journal of Research and Development, 2005, 49(2/3): 265-276.

Conditionalstrongmatchingpreclusionfork-aryn-cubes

FENG Kai*

(SchoolofComputer&InformationTechnology,ShanxiUniversity,TaiyuanShanxi030006,China)

To measure the ability ofk-aryn-cube to remain the property of having a perfect matching or an almost perfect matching in the presence of failures, by analysis of constructions of the fault sets that make thek-aryn-cube having neither a perfect matching nor an almost perfect matching under the conditional fault model, the minimum number of failures that make thek-aryn-cube unmatchable under the conditional fault model was studied. Whenk≥4 is even andn≥ 2, the exact value of the fault-tolerant parameter fork-aryn-cube was obtained and all the corresponding minimum fault sets were characterized. Whenk≥3 is an odd number and n≥2, a sharp lower bound and a sharp upper bound on the fault tolerance parameter fork-aryn-cube were given. The results indicate that the parallel computer system, which takes thek-aryn-cube with oddkas underlying interconnection topology, has good ability to remain the property of having a perfect matching or an almost perfect matching under the conditional fault model. Moreover, this system is still matchable if the number of failures does not exceed 2nand at most 4n-3 failures could make this system unmatchable.

parallel computer system; interconnection network;k-aryn-cube; perfect matching; conditional failure

2017- 03- 10;

2017- 04- 27。

国家自然科学基金资助项目(61502286)。

冯凯 (1987—)，男，山西临汾人，讲师，博士，CCF会员，主要研究方向：互连网络的容错性、图论及其应用。

1001- 9081(2017)09- 2454- 03

10.11772/j.issn.1001- 9081.2017.09.2454

TP393.02

A

This work is partially supported by the National Natural Science Foundation of China (61502286).

FENGKai, born in 1987, Ph. D., lecturer. His research interests include fault-tolerance of interconnection networks, graph theory and its applications.