透彻理解定义,巧妙解决难题
贺静


[摘 要] 数学中的概念定义是我们学习数学知识、研究数学理论、进行逻辑推理的基础,在教学中,学生解题的技巧灵活性不仅仅来源于对公式定理、通性通法的理解和把握,在透彻理解定义的基础上,同样可以巧妙解决难题.
[关键词] 概念定义;技巧灵活性;透彻理解
在数学家波利亚的《怎样解题》这本书中,有一个著名的怎样解题表,表中有一句经典的“回到定义去”. 这句经典的话如果能够理解并应用得好,对我们的教学将起到事半功倍的效果,尤其是在当今大力提倡减负增效的时候,我们更应该注意这方面的训练. 各种杂志中关于这方面的研究文章已经很多了,本文仅就初中数学教学中有关问题的解决再做一个浅解,希望在教学中能够进一步提升对学生数学能力的培养.
巧妙利用定义解决“超范围”难题
数学教学,让学生学会解题是其中的一个重要方面,最基本的要求是要学生会用和善于用所学数学知识和方法解决数学问题. 在这里,我们更希望看到的是学生的巧解和灵活应用,而个别老师喜欢把后面的知识或者数学结论拿来提前讲,然后让学生记忆和模仿,以期用所谓的简便方法解决问题,这是很不好的,不利于学生数学思维的培养,也不利于学生解题能力的提高. 笔者认为,需要给学生讲的应该是怎样用现有知识和方法,巧妙地解决一些复杂的甚至“超范围”的难题.
其实,不仅如此,许多看似复杂的问题,如果我们注意相关定义,也会迎刃而解.
用定义解决函数与方程的综合题
有些综合题目,看似很复杂,无从下手,但如果我们注意有关定义,注意它们之间的相互联系,问题往往能够迎刃而解.
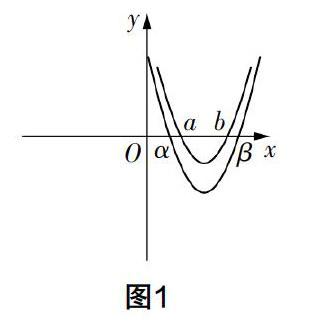
例2 设y=(x-a)(x-b)-3(a,b是实数,a<b),方程y=0存在两个不相等的实根α,β(α<β).
(1)若a+b=-4,a·b=3时,求α,β之值,并求函数在α≤x≤β时y的取值范围;
(2)试把a,b,α,β按从小到大的顺序排列出来,并说明你的排序理由.
本题作为初三后期复习考试的一次联合考试试题,第(2)小题的得分率非常低,大部分同学不知道如何下手,个别同学展开用求根公式讨论. 其实,注意题目条件:方程y=0存在两个不相等的实根α,β(α<β),为什么用这样一种表示方式?再联想方程根的定义,即y=0时x的取值,也就是函数图像与x轴的交点的横坐标,于是得解法如下:
因为y=(x-a)(x-b)-3,令y1=y+3=0,则a,b为y1=0的两根,因为y1的图像是将y的图像向上平移3个单位得到,y1和y的草图如图1所示,所以α<a<b<β.
本题的成功关键是用几何意义解题.
例3 如图2,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使DP-AP最大.
这题的第(2)小题许多考生不知道如何证明,而在一些官方给出的答案是:求出点A,B与D的坐标,然后求出直线方程,利用斜率乘积等于-1而得到垂直,得到切线的证明. 而这些都是高中数学要求的,初中都没有涉及. 为此,看着好像是超范围了,但研究以后可以发现另一种解法,如下:
其实,初中勾股定理是要求学生掌握好的,利用勾股定理及相关知识就可以轻而易举地解决. 而要证明直角,自然就是要看是不是有一边的平方是另外两边的平方和,于是计算有关三角形的边长的平方是关键.
如图2,过点D分别作x轴、y轴的垂线,交x轴、y轴于H,G两点,因为D(-6,-5),所以H(-6,0),G(0,-5),于是AH=10,DH=5,DG=6,BG=8.由勾股定理可得BD2+AB2=AD2,从而垂直得证. 这样所用到的知识点极少,也不需要用两点间距离公式,因为两点间距离公式也不是初中课程标准统一要求的,但勾股定理是必须掌握的. 至于AH,BG等长度,作为初中生来说是必须掌握的,而作为点的坐标的原始定义,就需要从各点引坐标轴的垂线,因此这种解法是每个初中生都应该掌握好的.
用定义解决一类几何计数问题
给初一学生讲解有关几何计数问题往往令许多老师为难,觉得不好讲,学生也不好接受. 下面我们从相关定义入手来解决,我们还会发现,以下系列题目的解决方法基本上是一模一样的.
例4 一直线上有n个点,以这些点为端点的线段有多少条?
分析:每条线段有两个端点,解决的突破口就在这里. 因为每个点可以和另外的一个点组成一条线段,这样,每个点都可以和另外n-1个点中的每一个组成一条线段,但对于一条线段来说,可以分别从两个端点来计算,故结果要除去重复计算的,应该是1/2n(n-1).
与此类似,平面上有n个点,以这些点为端点的线段也是1/2n(n-1)条.
例5 我们知道,两条直线被第三条直线所截,可以形成4對同位角,请问,在平面上n条直线两两相交,无三线共点,可以形成多少对同位角?
这题看似很难做,也有一些老师研究过其解法,但给出的解法学生都很难理解. 在思考之初,部分同学想归纳出来,发现n=3时,是12对,n=4时,是48对,没有办法数,更不好找规律. 其实,如果我们注意同位角的定义所指:“两条直线被第三条直线所截,可以形成4对同位角”,只要能够把这些直线这样分开,分成一个个独立不重复的“两条直线被第三条直线所截”的“三线小组”,问题就迎刃而解了:
每条直线与另外的n-1条直线中的任意一条都可以形成一个两条直线组合,剩下的n-2条中的每一条都可以用来截这个两条直线组合;而这样的两条直线组合有1/2n(n-1)个,总的就有这样的“三线组合”1/2n(n-1)(n-2)个,同位角就有4×1/2n(n-1)(n-2)=2n(n-1)(n-2)对.
当然,我们也能同时得到:在平面上n条直线两两相交,无三线共点,可以得到同旁内角和内错角都是n(n-1)(n-2)对.
用这种思考方式,我们很容易得到:n条直线交于一点共有n(n-1)对对顶角.
可见,这类计数问题都可以用这种方式来解决,突破口都是相关定义的理解并应用.
正如著名数学家、首届国家级数学名师李尚志先生在他的《数学的神韵》中所说:“人们总认为数学是烦琐的、复杂的. 数学当然有算法,算法也许是烦琐的,具体过程更是烦琐. 但是,指挥这些算法的想法一定是简单的,这才是最有威力的. ”而要达到这样的境界,就必须要真正理解有关数学概念,把用定义解题做到极致.
总之,如果我们能够真正理解有关数学概念的定义,能够真正理解数学知识、方法与数学问题之间的本质联系,学数学和做数学就会其乐无穷,学生自然能够将数学学得很好. 这样给学生讲解数学,也远比进行题海战术效果好得多.

