一类分数阶微分方程三点边值问题正解的存在性与不存在性
何健堃, 贾 梅, 陈 辉
(上海理工大学 理学院, 上海 200093)
0 引 言
分数阶微积分理论在物理、 化学和工程技术等领域应用广泛, 目前已受到广泛关注[1-3]. 关于分数阶微分方程边值问题的研究已取得了很多成果[4-16]. Su等[7]研究了非齐次边界条件分数阶微分方程两点边值问题:
正解的存在性和不存在性, 其中: 1<δ<2;J=(0,1]; 扰动参数a≥0,b≥0.
本文考虑分数阶微分方程关于含扰动参数的三点边值问题:
(1)
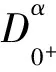
1)f(·,u)对u∈+是可测的;
2)f(t,·)对几乎处处t∈[0,1]是连续的;
3) 对每个r>0, 存在φr∈L1[0,1],φr(t)≥0, 使得|u|>≤r,t∈[0,1]时, 满足|f(t,tα-2u)|>≤φr(t).
文献[7]研究了非齐次边界条件下两点边值问题正解的存在性与不存在性, 通过假设非线性项f(t,u)是关于u的单调递增函数, 利用上下解方法、 Schauder不动点定理和不动点指数理论, 获得了该问题正解存在与不存在的充分条件. 由于非局部边值问题应用广泛, 因此本文考虑在边界条件中含有分数阶导数的三点边值问题正解的存在性与不存在性, 利用范数形式的锥拉伸与锥压缩不动点定理, 证明该问题在参数满足不同范围时正解的存在性与不存在性. 通过对扰动参数的控制, 得到了该问题正解存在性与不存在性的结果. 本文结果是在非线性项满足超线性与次线性条件下得出的, 因此不需要非线性项f(t,u)关于u单调递增的限制.
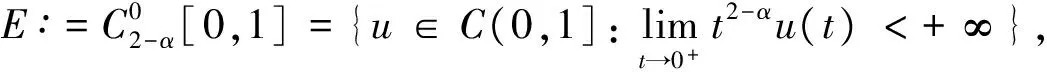
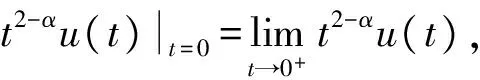
1 定义与引理
定义1[2]函数u: (0,∞)→的α阶Riemann-Liouville分数阶积分定义为
对任意的α>0, 右端积分在(0,∞)上逐点可积.
定义2[2]函数u: (0,∞)→的α阶Riemann-Liouville分数阶导数定义为
对任意的α>0, 右端积分在(0,∞)上逐点可积,n为大于或等于[α]的最小整数.
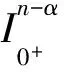
于[0,1]中几乎处处成立, 其中ci∈(i=1,2,…,n)为任意常数,n为大于或等于[α]的最小整数.
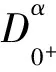
引理2记ρ=(1-λξα-β-1)-1, 对任意的y∈L1[0,1], 则边值问题
(2)
的唯一解可表示为
(3)
其中:
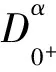
(6)
其中ci∈(i=1,2). 根据边界条件得c2=a, 则
(7)
因此, 将c1的值代入式(7), 则边值问题(2)的解为
其中G(t,s)和K(ξ,s)分别由式(4)和式(5)定义.
反之, 如果式(3)成立, 则易得u为边值问题(2)的解. 证毕.
引理3记H(t,s)=t2-αG(t,s), 则分别由式(4),(5)定义的函数G(t,s),K(ξ,s)和函数H(t,s)满足如下性质:
1) 对任意的t,s∈[0,1],G(t,s)是连续函数, 且G(t,s)≥0;

3) 对任意的t,s∈[0,1],H(t,s)是连续函数, 且H(t,s)≥0;
4) 对任意的t,s∈[0,1], 有
证明: 1) 由G(t,s)的表达式易知对任意的t,s∈[0,1],G(t,s)是连续函数, 且对任意的0≤t≤s≤1, 有G(t,s)≥0; 另一方面, 当0≤s≤t≤1, 有
因此, 结论1)成立.
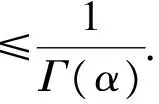
因此, 结论2)成立.
3) 由结论1)易知结论3)成立.
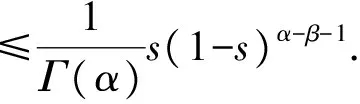
当0≤s≤t≤1时, 有
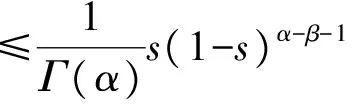
当0≤t≤s≤1时, 有
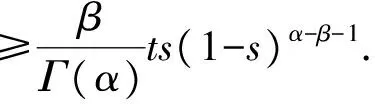
引理4(α-β-1)(λξα-β-2-1)+(α-1)ρ-1≥0.
证明: 如果λξα-β-2-1≥0, 即λ≥ξ2-α+β, 则不等式显然成立. 如果λξα-β-2-1<0, 即0≤λ<ξ2-α+β, 则有
当α-β-1-(α-1)ξ≥0时, 不等式显然成立; 当α-β-1-(α-1)ξ<0时, 有
λξα-β-2(α-β-1-(α-1)ξ)+β≥α-β-1-(α-1)ξ+β=(α-1)(1-ξ)≥0.
证毕.
定义P={u∈E:u(t)≥0,t∈(0,1]}, 显然P是E中的锥. 定义算子T:P→E, 则
令P0={u∈E:t2-αu(t)≥βt‖u‖,t∈(0,1]}, 则P0⊂P为E的一个锥.
引理5算子T:P→P0是全连续算子.
证明: 由引理3和引理4, 显然当u∈P时, 对任意的t∈(0,1], 有Tu(t)≥0, 且
另一方面, 由引理3, 有
则t2-αTu(t)≥βt‖Tu‖, 即T:P→P0.
令{un}⊂P,u0∈P, 且‖un-u0‖→0, 当n→+∞时, 存在常数l>0, 使得‖un‖≤l, ‖u0‖≤l. 则对任意的t∈[0,1], 有|t2-αun(t)|>≤l, |t2-αu0(t)|>≤l. 由f满足L1-Carathéodory条件可知, 对几乎处处s∈[0,1], 有
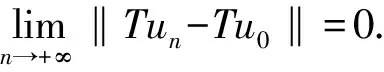
设Ω⊂P有界, 存在一个常数l>0, 使得对任意的u∈Ω, 有‖u‖≤l, 因此, 对任意的u∈Ω, 存在φl∈L1[0,1], 使得
|f(s,u(s))|>=|f(s,tα-2t2-αu(s))|>≤φl(s),s∈[0,1],
因此T(Ω)一致有界.
此外, 对任意的t,s∈[0,1], 因为G(t,s)是连续函数, 则其为一致连续函数, 因此对任意的ε>0, 存在常数
使得对所有的t1,t2,s∈[0,1], 当|t1-t2|><δ时, 有
从而
因此T(Ω)是等度连续的. 由Arzela-Ascoli定理可知,T(Ω)为相对列紧集. 从而T:P→P0是全连续的. 证毕.
由引理2, 易得:
引理6边值问题(1)存在一个正解当且仅当算子T在P中存在一个不动点. 此外, 若u是边值问题(1)的一个正解, 则u∈P0.
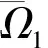
1) ‖Tu‖≤‖u‖,u∈P∩∂Ω1; ‖Tu‖≥‖u‖,u∈P∩∂Ω2;
2) ‖Tu‖≥‖u‖,u∈P∩∂Ω1; ‖Tu‖≤‖u‖,u∈P∩∂Ω2.
2 边值问题正解的存在性与不存在性
为方便, 记
定理1若f0
证明: 首先, 由于f0 故对任意的u∈∂Ω1, ‖Tu‖≤‖u‖. 根据引理3可得 故对任意的u∈∂Ω2, ‖Tu‖≥‖u‖. 定理2若f∞ f(t,tα-2u)≤φR1(t)+(M1-ε)u. 令 Ω3={u∈P0: ‖u‖ 且max{a0,b0}≤M1r3. 则对任意的u∈∂Ω3, 有‖u‖=r3, 并且 故对任意的u∈∂Ω1, ‖Tu‖≤‖u‖. 定理3若f∞>M2, 则存在a1,b1>0, 使得当a>a1,b>b1时, 边值问题(1)无正解. 令 因此 由式(5)和引理3可得 从而 即‖u‖>R. 即‖u‖>‖u‖+R, 矛盾, 假设不成立. 故存在正常数a1,b1, 使得当a>a1,b>b1时, 边值问题(1)无正解. 证毕. 例1考虑边值问题: (8) 可得以下结论: 1) 如果参数a∈[0,0.000 833 361 6),b∈[0,0.000 833 361 6), 则边值问题(8)至少存在一个正解. 2) 如果参数a∈[1.134×107,+∞),b∈[1.134×107,+∞), 则边值问题(8)不存在正解. 这里边值问题(1)中 α=5/3,β=1/2,ξ=4/5,λ=1,f(t,u)=t2/3u2arctantu+t1/2(1+sint)u3/2. 则存在φr(t)=r2arctant2/3r+(1+sint)r3/2, 使得对所有的u≤r及t∈(0,1), 有|f(t,t-1/3u)|>≤φr(t), 易见f满足L1-Carathéodory条件. 通过简单计算可得: M1=0.027 778 72,M2=264.884 7,f0=0 1) 令r1=0.03, 选取max{a0,b0} 2) 令R=3.14×106, 当u∈[3.925×105,+∞),t∈(0,1)时, 有f(t,t-1/3u)>M2u. 选取min{a1,b1}>4Γ(α)R=1.134×107. 由定理3可知, 当a,b∈[1.134×107,+∞)时, 边值问题(8)不存在正解. 例2考虑边值问题: (9) 这里边值问题(1)中α=3/2,β=1/3,ξ=3/5,λ=1,f(t,u)=etq/2uq, 0 [1] 白占兵. 分数阶微分方程边值问题理论及应用 [M]. 北京: 中国科学技术出版社, 2013. (BAI Zhanbing. Theory and Application of Fractional Differential Equation Boundary Value Problems [M]. Beijing: China Science and Technology Press, 2013.) [2] Podlubny I. Fractional Differential Equations [M]. San Diego, CA: Academic Press, 1999. [3] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations: North-Holland Mathematics Studies, Vol.204 [M]. Amsterdam: Elsevier, 2006. [4] 刘帅, 贾梅, 秦小娜. 带积分边值条件的分数阶微分方程解的存在性和唯一性 [J]. 上海理工大学学报, 2014, 36(5): 409-415. (LIU Shuai, JIA Mei, QIN Xiaona, et al. Existence and Uniqueness of Solutions of the Fractional Differential Equation with Integral Boundary Value Conditions [J]. Journal of University of Shanghai for Science and Technology, 2014, 36(5): 409-415.) [5] 窦丽霞, 刘锡平, 金京福, 等. 分数阶积分微分方程多点边值问题解的存在性和唯一性 [J]. 上海理工大学学报, 2011, 33(5): 51-55. (DOU Lixia, LIU Xiping, JIN Jingfu, et al. Existence and Uniqueness of Solutions of Multi-point Boundary Value Problems for Integro-Differential Equation of Fractional Order [J]. Journal of University of Shanghai for Science and Technology, 2011, 33(5): 51-55.) [6] 李晓晨, 刘锡平, 李燕, 等. 无穷区间上含参数分数阶微分方程积分边值问题正解的存在性 [J]. 吉林大学学报(理学版), 2017, 55(1): 13-21. (LI Xiaochen, LIU Xiping, LI Yan, et al. Existence of Positive Solutions for Integral Boundary Value Problems of Fractional Differential Equations with Parameters in Infinite Interval [J]. Journal of Jilin University (Science Edition), 2017, 55(1): 13-21.) [7] SU Xiaofeng, JIA Mei, LI Mengmeng. The Existence and Nonexistence of Positive Solutions for Fractional Differential Equations with Nonhomogeneous Boundary Conditions [J/OL]. Advances in Difference Equations, 2016-01-28. https://doi.org/10.1186/s13662-016-0750-5. [8] WANG Xiao, LIU Xiping, DENG Xuejing. Existence and Nonexistence of Positive Solutions for Fractional Integral Boundary Value Problem with Two Disturbance Parameters [J/OL]. Boundary Value Problems, 2015-10-12. doi: 10.1186/s13661-015-0450-1. [9] JIA Mei, LIU Xiping. The Existence of Positive Solutions for Fractional Differential Equations with Integral and Disturbance Parameter in Boundary Conditions [J/OL]. Abstract and Applied Analysis, 2014-03-24. http://dx.doi.org/10.1155/2014/131548. [10] Li C F, Luo X N, ZHOU Yong. Existence of Positive Solutions of the Boundary Value Problem for Nonlinear Fractional Differential Equations [J]. Computers and Mathematics with Applications, 2010, 59(3): 1363-1375. [11] Nyamoradi N, Baleanu D, Agarwal R P. Existence and Uniqueness of Positive Solutions to Fractional Boundary Value Problems with Nonlinear Boundary Conditions [J/OL]. Advances in Difference Equations, 2013-09-08. https://doi.org/10.1186/1687-1847-2013-266. [12] LI Bingxian, SUN Shurong, HAN Zhenlai. Positive Solutions for Singular Fractional Differential Equations with Three-Point Boundary Conditions [J]. Journal of Applied Mathematics and Computing, 2016, 52(1/2): 477-488. [13] ZHANG Xingqiu. Positive Solutions for a Class of Singular Fractional Differential Equation with Infinite-Point Boundary Value Conditions [J]. Applied Mathematics Letters, 2015, 39: 22-27. [14] LI Bingxian, SUN Shurong, ZHAO Ping, et al. Existence and Multiplicity of Positive Solutions for a Class of Fractional Differential Equations with Three-Point Boundary Value Conditions [J/OL]. Advances in Difference Equations, 2015-12-24. doi: 10.1186/s13662-015-0714-1. [15] ZHOU Wenxue, CHU Yandong, Băleanu D. Uniqueness and Existence of Positive Solutions for a Multi-point Boundary Value Problem of Singular Fractional Differential Equations [J/OL]. Advances in Difference Equations, 2013-04-19. https://doi.org/10.1186/1687-1847-2013-114. [16] LIU Xiping, JIA Mei, GE Weigao. The Method of Lower and Upper Solutions for Mixed Fractional Four-Point Boundary Value Problem withp-Laplacian Operator [J]. Applied Mathematics Letters, 2017, 65: 56-62. [17] 郭大钧, 孙经先, 刘兆理. 非线性常微分方程泛函方法 [M]. 2版. 济南: 山东科学技术出版社, 2006. (GUO Dajun, SUN Jingxian, LIU Zhaoli. Funtional Methods for Nonlinear Ordinary Differential Equations [M]. 2nd ed. Jinan: Shangdong Science and Technology Press, 2006.)
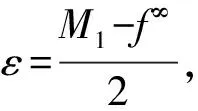

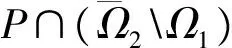
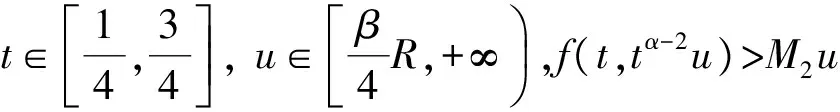
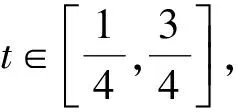
3 应用实例

