无限维量子系统上的保真度

段周波， 牛丽芳

(太原理工大学 数学学院， 山西 太原 030024)

1 研究背景

在量子力学中， 一个量子系统可描述为一个可分复希尔伯特空间H. 注意到量子态ρ∈B(H)是一个迹为1的正的迹类算子， 即ρ≥0且Trρ=1. 令S(H)表示所有H上的态的集合， 可知它是一个凸集. 保真度是量子光学和信息科学领域中非常重要的一个概念, 广泛应用于量子通信和量子计算, 它表示信息在传播过程中保持原来状态的程度. R.Jozsa等[1-2]首先提出保真度的概念， 其定义式为

当dimH=n<∞, Uhlmann[3-4]证明了F(ρ,σ)=max|〈φ|φ〉|， 其中φ,φ是ρ,σ相应的纯化， 最大值在ρ,σ的所有纯化上取得， 这个性质叫做Uhlmann定理. 另外， 在量子编码术以及信息传递过程中， 为了描述量子信息的保真度， 研究者又定义了两类重要的保真度： 纠缠保真度和系综平均保真度[5-7]. 假设R和Q是两个量子系统， dimQ=n<∞, 系统R是孤立的， 与外界没有任何形式的能量交换， 其内部的哈密顿量为0. 在初始时刻， 系统Q被制备在ρQ态， 在复合系统RQ上纯化ρQ， 得到一个纠缠纯态|ψRQ〉， 经过信道IR⊗ΦQ的作用， 最后的末态可能是复合系统RQ上的一个混合态， 用ρRQ′来描述， 而在这个信息传递过程中的保真度

Fe=Tr|ψRQ〉〈ψRQ|ρRQ′=〈ψRQ|ρRQ′|ψRQ〉,

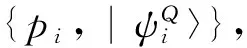
近来， 学者在无限维量子系统中对保真度展开了一定的研究. 无限维量子系统(包括连续变量系统)在量子通信与量子信息理论中起着巨大的作用[8-13].Hou等[14]将量子保真度的概念推广到无限维情形， 并证明了Uhlmann定理在无限维情形中依然成立， 并将其称之为无限维版本的Uhlmann定理. 紧接着，Wang等[15]将纠缠保真度的概念推广到了无限维情形， 并在无限维情形中对纠缠保真度和量子保真度进行了深入地探讨和比较.

本文在无限维量子系统中， 利用无限维版本的Uhlmann定理， 探讨了量子保真度的一些基本性质， 并且证明了纠缠保真度与量子态的纯化的选择无关这一重要性质， 最后研究了纠缠保真度和系综平均保真度的关系.

2 主要结论及证明

引理 1 (无限维Uhlmann定理)[14]设H和K是两个无穷维复希尔伯特空间， 对H上任意两个态ρ和σ， 有

F(ρ,σ)=max{|〈φ|ψ〉|2∶|φ〉∈Pρ,|ψ〉∈Pσ},

其中Pρ={|φ〉∈H⊗K∶|φ〉是ρ的一个纯化}.

定理 1 (无限维保真度的强凹性) 设H是一个无穷维复希尔伯特空间， {pi}和{qi}是两个概率分布， {ρi}和{σi}是H上相应的两列量子态， 则

〈φ|ψ〉|2=

利用定理1， 很容易得到下面的推论：

推论 1 (无限维保真度的联合凹性) 设H是一个无穷维复希尔伯特空间， {pi}是一个概率分布， {ρi}是H上相应的一列量子态， 则

推论 2 (无限维保真度的凹性) 设H是一个无穷维复希尔伯特空间， {pi}是一个概率分布， {ρi}是H上相应的一列量子态， 且σ是H上的一个量子态， 则

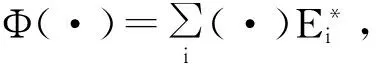
引理 2[16]设R和Q是两个无穷维量子系统， 主系统Q上有一个初始量子态ρQ和一个量子信道ΦQ. 若|φ1〉和|φ2〉是初始态ρQ的两个纯化， 它们经过动力演化IR⊗ΦQ之后相应的末态为ρ1和ρ2， 则存在辅助系统R上的一个等距算子VR， 使得ρQ的两个纯化满足下面两个公式之一： |φ1〉=(VR⊗IQ)|φ2〉 或者|φ2〉=(VR⊗IQ)|φ1〉； 它们相应的末态满足相应的公式：ρ1=(VR⊗IQ)ρ2(VR⊗IQ)*或者ρ2=(VR⊗IQ)ρ1(VR⊗IQ)*.

定理 2 设Q是一个无穷维量子系统， 其上有一个初始量子态ρQ和一个量子信道ΦQ， 则纠缠保真度Fe与ρQ的纯化的选择无关.

证明 假设|φ1〉和|φ2〉是ρQ的两个纯化， 它们经过动力演化IR⊗ΦQ之后相应的末态为ρ1和ρ2， 由引理2， 不失一般性地可假设|φ2〉=(VR⊗IQ)|φ1〉成立， 此时

ρ2=(VR⊗IQ)ρ1(VR⊗IQ)*,

这样

Fe2=〈φ2|ρ2|φ2〉=〈φ1|(VR⊗IQ)*

(VR⊗IQ〉ρ1(VR⊗IQ)*(VR⊗IQ)|φ1〉=

〈φ1|ρ1|φ1〉=Fe1,

表明纠缠保真度Fe与ρQ的纯化的选择无关.

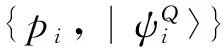
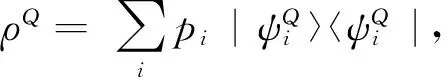
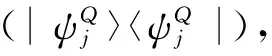
根据强算子拓扑， 可知ΘRQ收敛于HR⊗HQ的子空间上的一个投影

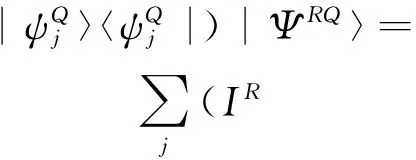
于是有算子不等式ΘRQ≥|ΨRQ〉〈ΨRQ|. 对于所有的正的迹类算子TRQ, 显然Tr[(ΘRQ-|ΨRQ〉〈ΨRQ|)TRQ]≥0, 即Tr(ΘRQTRQ)≥Tr(|ΨRQ〉〈ΨRQ|TRQ). 注意到

于是

Fe=Tr|ΨRQ〉〈ΨRQ|ρRQ′≤TrΘRQρRQ′=

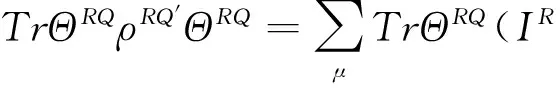
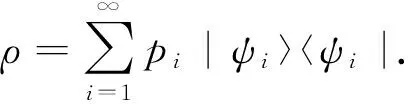
3 结 论

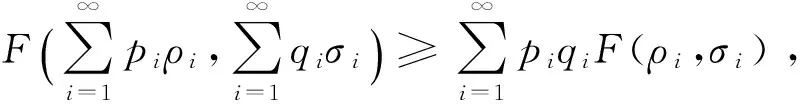
[1]NielsenMA,ChuangIL.Quantumcomputationandquantuminformation[M].Cambridge:CambridgeUniversityPress, 2000.

[2]JozsaR.Fidelityformixedquantumstates[J].JournalofModernOptics, 1995, 41(12): 2315-2324.

[3]UhlmannA.The“transitionprobability”inthestatespaceofa*-algebra[J].ReportsonMathematicalPhysics, 1976, 9(2): 273-279.

[4]UhlmannA.Transitionprobability(fidelity)anditsrelative[J].FoundationsofPhysics, 2011, 41(3): 288-299.

[5]SchumacherB.Quantumcoding[J].PhysicsReviewA, 1995, 51(4): 2738-2747.

[6]SchumacherB.Sendingentanglementthroughnoisyquantumchannels[J].PhysicsReviewA, 1996, 54(4): 2614-2628.

[7]SchumacherB,NielsenMA.Quantumdataprocessinganderrorcorrection[J].PhysicsReviewA, 1996, 54(4): 2629-2640.

[8]HolevoAS.Quantumsystems,channels,information[M].Berlin:WalterdeGruyterGmbH, 2012.

[9]郭钰. 量子关联的数学刻画[M]. 北京: 科学出版社, 2016.

[10]郭钰. 无限维两体复合系统量子态的纠缠判据[D]. 太原: 山西大学, 2011.

[11]阎思情. 无限维多体复合量子系统量子态的纠缠判据[D]. 太原: 太原理工大学, 2013.

[12]王丽. 无限维量子系统上的信道、 保真度及相关问题研究[D]. 太原: 太原理工大学, 2015.

[13]段周波. 无限维系统上的信道、 熵交换及相关问题研究[D]. 太原: 太原理工大学, 2017.

[14]HouJC,QiXF.Fidelityininfinite-dimensionalquantumsystems[J].ScienceChinaPhysicsMechanics&Astronomy, 2012, 55(10): 1820-1827.

[15]WangL,HouJC,QiXF.Fidelityandentanglementfidelityforinfinite-dimensionalquantumsystems[J].JournalofPhysicsAMathematical&Theoretical, 2014, 47(33): 33530.

[16]DuanZB,HouJC.Entropyforexchangeinfinite-dimensionalsystems[J].SciencificReports, 2017, 7: 41692.