基于动态特性的横梁结构优化设计
邝泳聪,洪海生,梁经伦 ,李家裕
(1.华南理工大学机械与汽车工程学院,广东 广州 510640) (2.东莞理工学院机械工程学院,广东 东莞 523808)
面向异型元件的异型插件机,国外的研发始于20世纪80年代,真正在国内推广是2010年左右。异型电子元器件的质量和体积都较大,在高速来回运动状态下要实现高精度准确插件,横梁的动刚度尤为关键。不同的横梁结构决定了横梁不同的质量、抗弯曲强度、固有频率和振动幅值,横梁在设计时必须避开可能的共振频率。
在相关研究方面,张森等[1]对4种常见截面形状的龙门式加工中心横梁进行对比,分别从静态特性和动态特性等角度进行了分析。姜涛等[2]通过刚柔耦合动力学分析方法,对横梁的腹板孔形状进行优化,以贴装头的时域振动曲线和加速度曲线的变化情况评价横梁结构性能。孙继斌等[3]对贴片机横梁的内外部结构参数进行对比分析,比较横梁的前三阶固有频率。王艳青等[4]对联动加工中心横梁进行静力学分析,通过设计横梁筋板结构,对比设计最优结构。关英俊等[5]对龙门加工中心横梁的加强筋进行增强,通过模态分析的固有频率比较,从而改进横梁设计。周德繁等[6]对龙门镗铣床横梁进行静力学分析,基于分析结果对横梁尺寸和结构进行了优化。
本文的优化对象为某型号异型插件机横梁,借助ANSYS有限元软件[7]和ADAMS多体动力学软件[8],以横梁固有频率和振动时域曲线的振幅来评价横梁的动态特性,从而优化横梁结构、减轻横梁质量和改善其动态特性。
1 动态特性分析
1.1 有限元模态分析
结构的固有频率直接影响到系统的动态性能。结合实验模态测试,对自由状态下的横梁进行锤击法模态测试实验,从而验证有限元模态分析的可靠性。横梁的自身动态性能的优化是研究目标,在约束状态下,通过对不同截面横梁的有限元模态分析,比较不同模态频率值,从而不断优化横梁的动态性能。
1.1.1结构固有频率和主振型
无阻尼自由振动的动力学基本方程为:

(1)
式中:M为质量矩阵;K为刚度矩阵;δ(t)为时间位移函数矩阵。
把自由振动分解为一系列简谐振动的叠加,将简谐振动方程代入式(1)中,则无阻尼自由振动方程为:
(K-ω2M)δ0=0
(2)
式中:ω为对应阶数的固有频率;δ0为相对应时刻的位移函数。求解微分方程(2)的特征值,则求得结构的固有频率。
1.1.2自由锤击法模态测试实验
使用PCB力锤对自由状态下的横梁进行激振。锤头内置的力传感器和安装在横梁上的加速度传感器同步记录下瞬态激励和被测对象的响应,经信号分析仪ZonicBook/618E采集处理;数据采集后传输到计算机进行计算分析。本文采用ME'scope模态分析软件对数据进行模态分析,获取被测对象的模态频率及阻尼,如图1所示。整个测量系统包含横梁、力锤、加速度传感器、动态信号分析仪、计算机及信号线等。

图1 测量系统体系
本文所研究的横梁材质为铝合金,通过铸造工艺而成。实验中采用“自由-自由”边界条件的方式,在横梁上布置7个压电式加速度传感器,激励方式通过SIMO的方式,使用力锤在每个激励点锤击10次。通过eZ-Analyst软件收集8个通道的数据,将FRF文件导入到ME'scope模态分析软件中,从而算出6阶模态及相应阻尼。
进行相应的测试后,进行ANSYS有限元分析,对应实验测试的固有频率见表1。

表1 有限元分析与模态测试结果对比表
表中的实验数据表明,力锤自由模态测试实验的测试结果与仿真结果较为接近,最大误差出现在第5阶模态,为20.0%;而由于某些激励点和响应点的选取不当以及敲击的力度和速度的控制等原因,出现一阶模态丢失。
1.2 横梁的刚柔耦合动力学分析
为了更好地研究横梁在运动过程中的变形,首先借助刚柔耦合动力学分析技术,在ANSYS经典界面里生成横梁的模态中性文件,其中横梁单元用solid186三维单元,刚性节点用mass21单元定义;其次在SolidWorks中建立整机局部三维模型,如图2所示,导入到ADAMS中;最后将横梁刚形体替换为横梁的模态中性文件,对模型进行相应的约束和相应驱动函数的编辑,从而实现刚柔耦合动力学模型的建立。

图2 整机局部三维模型
1.2.1ADAMS中的多刚体动力学方程
(3)
Φi=0
(4)
式中:K为系统的总动能;qi为系统的广义坐标;Φi为系统的约束方程;Fi为广义坐标上的广义力;λi为拉氏乘子。
在求系统的总动能解出K后,代入微分方程(3),由式(3)、(4)求解出刚体的位移、速度、加速度、受力等。
1.2.2ADAMS中的多柔体动力学方程
(5)
Ψ=0
(6)
式中:Ψ为约束方程;λ为对应于约束方程的拉氏乘子;ε为广义坐标;Q为投影到ε上的广义力;L为拉格朗日项;Γ为能量损耗函数。
求解L,Γ后,代入式(6)中,得到微分方程:
(7)
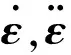
2 横梁结构优化
2.1 开孔形状优化
现有的横梁结构形状,其中心部分的截面为圆形。本文设计了其他4种常见的截面,分别为叉形截面、菱形截面、三角形截面和田字形截面,如图3所示。对比计算5种不同截面形状横梁的固有频率,同时结合异型插件机的运动特性,比较主要振型所对应固有频率的差异,从而进行相应的动态特性比较,选择更合适的截面。

图3 不同截面的横梁
在ANSYS中求出实际约束状态下5种不同截面的横梁模型的前6阶固有频率,具体见表2。

表2 5种截面的模态频率比较
横梁的实际运动情况是横梁装载着插件头做加减速运动,最大加速度为2g,横梁受到X方向惯性力的作用产生变形,对应的变形情况在工程中比较受关注。其中横梁第一阶振动频率尤为关键。对比各种截面的一阶频率,本文设计的4种截面横梁模型的一阶频率都比圆形截面横梁模型的一阶频率高,同时质量都比原横梁模型质量小。其中,田字形截面横梁的质量较圆形截面横梁减轻2%,一阶模态也提高约2%。
2.2 质量分布优化
为了提升横梁的刚性,对横梁滑轨安装面进行尺寸优化。如图4所示,在X方向,定义L1为平台板基准面到平台板滑块安装面的距离;L2为直线导轨的安装高度;L3为横梁滑轨安装面到横梁丝杆安装面的距离;L为平台板基准面到横梁丝杆安装面的距离,L=L1+L2+L3。在Z方向上,横梁的跨度约为插件头部的4倍。建立优化函数:

(8)
s.t. 0≤x≤15,且x为整数
式中:x为L3的减少量。

图4 横梁与插件头部位置关系
该优化设计问题属于整数规划,分别令x=10mm和x=15 mm,即L3分别减少10mm和15mm建立横梁的优化模型,优化模型的质量与原模型相比大大减小,其具体数值见表3。

表3 模型设计参数及质量
注:↑表示增加,↓表示减少。
在ADAMS中建立相应的刚柔耦合动力学模型,对动力学模型分别施加2.0g、2.5g和3.0g的加速度,运动周期为0.3s,进行仿真。其中3.0g加速度仿真两个运动周期的驱动函数为:
step(time,0,0,0.08,32 400d)+step(time,0.08,0,0.22,0)+step(time,0.22,0,0.3,-32 400d)+step(time,0.5,0,0.58,32 400d)+step(time,0.58,0,0.72,0)+step(time,0.72,0,0.8,-32 400d)
该横梁的主要敏感方向为X方向。分析整理仿真数据,对比在一个运行周期内,横梁在不同加速度驱动下,其在敏感方向上的动态变形情况。具体如图5所示。

图5 不同加速度下各模型的参数比较
由图可以看出,两优化模型的动态变形量与原模型相比均有所优化,不同的加速度工况下,两优化模型的动态变形都小于原模型的动态变形。例如在2g的加速度下,横梁质心在X方向的最大动态变形量为0.013 0mm,而两个优化模型的最大动态变形量分别为0.005 3mm和0.004 8mm,分别减少了59%和63%。同时优化后横梁的质量分别比原来的横梁减少12%和17%。从图中还可看出,随着加速度的增加,横梁的动态变形量也随着增大。
2.3 加强筋布置优化
对横梁结构的相关分析表明,相比于均匀分布的横梁,不均匀结构的横梁可能会有更好的质量分布和强度,能满足特定功能应用场合的需要。现根据横梁的受力情况,在横梁刚度较小的地方保持现有的加强筋,而对其他刚度较大的地方,减少相应的加强筋,实现横梁质量的减小。据此设计以下两种不同结构形式的横梁,如图6所示。运用刚柔耦合动力学,对比这两种模型与原有的横梁在不同的加速度下,其质心在X方向的最大位移量。

图6 加强筋不同布置的横梁
在ADAMS中,建立刚柔耦合动力学模型。通过施加不同的加速度2.0g、2.5g和3.0g的驱动函数,进行仿真模拟,结果如图7所示。

图7 横梁质心振动时域变形
分析比较以上两种优化模型与原有模型在X方向上横梁质心点上的变形情况。整理数据后的比较结果如图8所示。

图8 不同加速度下各模型的参数比较
两种优化模型,结构上是通过减少加强筋的数量,同时改变截面形状,从而达到减少横梁质量的目的。从图中数据可知,优化模型3和横梁原型的变形量较为接近,在2g加速度的情况下,优化模型3比横梁原型在质量上减少4%,而变形量增大了4.5%;优化模型4,在质量上减少6%,而变形量增大了28%。从对比中可以发现,加强筋对横梁的刚度起着重要的作用。随着加速度的增大,横梁的动态性能逐渐降低,横梁变形加大。
3 结论
1)自由模态测试结果与有限元分析结果较为接近,最大误差为20%。5种中心部分截面形状不同的横梁,在约束状态下,田字形横梁的质量较原横梁减轻2%,一阶模态也提高约2%。
2)对横梁的负载情况进行分析后,在保证总安装尺寸L不变的前提下,减小L3,增加L1,实现质量的优化分布。在2g的加速度下,横梁的变形量分别减少了59%和63%,其质量分别减少了12%和17%。若使用改进后的模型,横梁的运行加速度可以从2g提高到3g,插件效率可以大大提高,同时插件精度也可有所提高。
3)减少加强筋数量的同时改变截面形状对横梁进行优化,通过ADAMS和ANSYS联合仿真结果表明,其中一个优化模型的质量和横梁变形量与原横梁相差不大,可视情权衡取舍;另一个优化模型在2g的加速度下,质量减少6%,但变形量却增大了28%,选择时需要慎重考虑该优化方案。通过研究可以发现,加强筋对横梁的静刚度和动刚度有着重要的影响。
[1] 张森,杨玉萍,季彬彬,等. 龙门加工中心横梁结构设计与分析[J]. 机械设计与制造, 2013(10):32-35.
[2] 姜涛,唐火红,冯宝林. 拱架式贴片机横梁刚柔耦合动态仿真优化设计[J]. 机械设计与制造, 2014(6):31-34.
[3] 孙继斌,骆敏舟,姜涛,等. 高精度贴片机横梁结构动态优化设计[J]. 机械设计与制造, 2014(8):45-51.
[4] 王艳青,仲高艳,常永标,等. 大型五轴联动加工中心横梁结构设计[J]. 机床与液压, 2012, 40(13):114-120.
[5] 关英俊,母德强,赵扬,等. GMCU2060龙门加工中心横梁结构有限元分析[J]. 机床与液压,2011,39(11):131-134.
[6] 周德繁,高炳微,智政. 重型龙门镗铣床横梁有限元分析与结构优化[J].哈尔滨理工大学学报,2013,18(2):72-76.
[7] 商跃进. 有限元源于与ANSYS应用指南[M]. 北京:清华大学出版社, 2005.
[8] SHABANA Ahmed A. Dynamic of Multibody Systems[M].3rd ed. New York:Cambridge University Press,2005.

