基于明暗恢复形状的三维重建改进算法

刘 远，孙 进，聂庆玮

(扬州大学机械工程学院，江苏 扬州 225127)

基于单张照片进行目标物体的三维重建是计算机视觉的一个热点研究问题，目前使用较多的一种方法是明暗恢复形状(shape from shading,SFS)方法[1]，SFS在没有约束的条件下是一个病态问题，需要已知光源方向和假定朗伯反射模型。然而这些约束条件往往只能在实验室里才能实现，现实条件下根本无法解决[2-3]。本文提出一种基于球面谐波原理的改进算法，可以在未知光源方向的条件下进行三维重建。

1 基于单张照片的三维重建方法

基于单张照片的三维重建是目前机器视觉领域研究的热点，在人脸识别、虚拟现实以及颜面修复等领域都有着广阔的应用前景。当下主流的重建方法大致可归为SFS、神经网络以及形变模型3种。

SFS方法是一个欠约束问题，未知的是物体表面的两个定向自由度，已知条件只有表面亮度值这一个信息。SFS方法最大的优势是简单的重建条件(单张照片)以及快速的重建过程。但在重建过程中，需要假设朗伯反射模型以及已知的光源方向，同时待重建物体表面要求连续。

为了克服SFS方法严格的约束条件，神经网络和形变模型方法应运而生。神经网络方法的本质就是构建出一个更符合现实条件的反射模型[4]，通过神经网络训练，无需已知光源方向就可以进行三维重建，但对于较为复杂的物体，效果往往并不理想。形变模型方法一般用于人脸重建，首先利用数据库中的人脸数据信息构建一般的标准人脸模型，在之后的重建过程中利用标准人脸模型约束三维重建过程[5]。虽然形变模型方法可以达到较高的精度，但需要数据库这一先验知识，给重建带来了诸多不便。

2 三维重建改进算法

根据分析，本文选用SFS方法进行三维重建，并在原有算法的基础上进行改进。SFS方法是根据输入图像像素点的亮度来恢复图像的深度信息，由此达到2D到3D的信息扩展[6-8]。本文提出的基于球面谐波的改进算法不需要已知光源方向。朗伯模型是理想的反射模型，当一束平行光射到朗伯模型表面时，每个像素点的亮度由Lambert 余弦定理得出：

I(x,y)=ρ(x,y)⎣b(x,y)Ts」

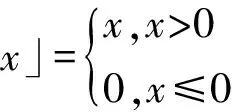
在任意光照条件下，照片中凸状朗伯物体的像素点亮度可有效地近似为：

I(x,y)≈f(x,y)Ts′

在一个4维或者9维的线性子空间，f(x,y)是4个或者9个最低的点(x,y)表面法向量的球面谐波系数，s′是光照条件的球面谐波系数。基于光沿所有方向的反射都是等可能的这一假设，在4维或者9维空间中球面谐波的近似度分别可达到87.5%和99.2%。因此，在重建过程中可利用球面谐波原理，使一般光照条件能够近似替代理想光照条件。

为了提高重建精度，将光源分为环境光与辐射光。考虑到重建对象的差异性，特别地将重建对象的反射模型分为漫反射与镜面反射，漫反射模型就是朗伯反射模型，整个三维重建过程如图1所示。

图1 三维重建过程

3 实验与结果

本文使用C++语言搭建了基于对话框的MFC应用程序，输入为待重建物体的单幅正面照片。应用程序框架的菜单栏上有照片输入和光源与反射模型的选取。图2为照片输入和光源与反射模型选取的界面。

图2 照片输入和光源与反射模型的选取

由于不同物体表面的反射特性不同，当光投向光滑物体的表面时，光会沿平行方向反射，即镜面反射；而当光投向凹凸不平的表面时，光会沿各个方向反射，即漫反射。将两类物体区分对待有利于提高物体三维重建的精度。通过实验得出的结果显示，在未知光源方向的情况下，改进的算法可以有效地重建目标物体的三维信息且在精度上有一定的保证(如图3、图4所示)。

图3 漫反射模型重建结果

图4 镜面反射模型重建结果

4 结束语

本文提出的基于明暗恢复形状的改进算法，基于球面谐波原理可用一般光照条件替代特定光照条件，解除了光照约束，可以在未知光源方向的前提下进行基于单张照片的三维重建。实验结果表明，该算法对未知光照条件物体的三维重建有着良好的适应性，并且在重建过程中针对不同的反射物体区分为漫反射模型和镜面反射模型，有效地提高了重建精度，对明暗恢复形状方法的实际应用具有重要意义。

[1] ZHANG R,TSAI P S,CRYER J E, et al．Shape from shading:a survey[J]．IEEE Transactions on Pattern Analysis & Machine Intelligence,2002,21(8):690-706.

[2] PRADOS E,FAUGERAS O．Shape from shading:a well-posed problem?[J]．IEEE Computer Society Conference on Computer Vision and Pattern,2005,2(1):870-877.

[3] NG H S,WU T P,TANG C K．Surface-from-gradients without discrete integrability enforcement:a gaussian kernel approach[J]．IEEE Transactions on Pattern Analysis & Machine Intelligence,2010,32(11):2085-2099.

[4] MALIK A S,CHOI T S．Effect of noise and source illumination on 3D shape recovery[J]．International Journal of Pattern Recognition & Artificial Intelligence,2008,22(5):945-958.

[5] OLIVEIRA-SANTOS T,BAUMBERGER C,CONSTANTINESCU M,et al．3D face reconstruction from 2D pictures: first results of a web-based computer aided system for aesthetic procedures[J]．Annals of Biomedical Engineering,2013,41(5):952-966.

[6] 仇开金．基于单幅图像明暗恢复形状算法设计[J]．计算机与现代化,2010(6):58-60.

[7] BISWAS S,AGGARWAL G,CHELLAPPA R．Robust estimation of albedo for illumination-invariant matching and shape recovery[J]．IEEE Transactions on Pattern Analysis & Machine Intelligence,2009,31(5):884-899.

[8] 吴侨．基于单张照片的三维人脸重建的研究[D]．成都：电子科技大学, 2016.

[9] LEE M,CHOI C H．Fast facial shape recovery from a single image with general, unknown lighting by using tensor representation[J]．Pattern Recognition,2011,44(7):1487-1496.