绞吸挖泥船横移过程的预测控制系统研究
魏长赟,倪福生,戴 伟,蒋 爽,陈秀静
(河海大学疏浚技术教育部工程研究中心,江苏 常州 213022)
挖泥船广泛应用于航道开挖、河湖疏浚、岛礁填筑等工程,已成为港口航道整治、江河湖库清淤、扩增土地面积的重要施工作业装备。绞吸挖泥船是主力疏浚船舶之一,用途广泛,其施工作业主要通过绞刀对水下土层进行横移切削,然后依靠安装在挖泥船上的离心泵使泥水混合物通过长距离排泥管输送到规定的抛泥区。疏浚作业时,横移切削是最为频繁的操作步骤,目前完全依赖驾驶员通过手柄进行操控[1-2]。为了使挖泥船产量相对稳定,操作人员需要根据长期疏浚作业积累的经验来操作横移手柄,调节横移速度。由于不同的环境、土质等对疏浚作业影响非常大,目前疏浚作业效率低下,经验依赖性强。
为了减少疏浚施工过程对人员的依赖,需要研制高效、精确、自动化程度高的横移过程控制系统。现阶段我国对横移过程自动控制系统的研发还处于初级阶段。唐建中等[3]以横移速度为控制输入,采用自校正方法对绞吸挖泥船的自动控制进行了初步研究。闭跃治[4]基于唐建中的控制模型提出了泥沙输送系统工况点的在线优化方法。李志刚[5]在倪福生等[6-7]对泥沙输送系统动态特性研究成果的基础上提出使用模糊PID控制方法设计横移控制系统。朱文亮等[8]提出了基于BP神经网络的横移过程状态空间建模方法,并使用二次型最优控制理论设计控制器。以上的控制系统均建立在理想的精确数学模型之上,但是横移过程动态特性非常复杂,各参数之间的关系不明确,所以使用以上模型对横移过程模型进行描述有一定的局限性。另外由于施工环境、土质、工况具备的不确定性,系统按照理想模型得到的最优控制往往不能保持最优,因此需要寻找更好的控制方案设计横移过程控制系统。
本文根据RBF-ARX(radial basis function-auto regressive exogenous)模型理论[9-11],基于挖泥船实测数据建立绞吸挖泥船横移过程模型,用以描述横移过程的全局动态特性,然后使用预测控制算法设计横移过程控制器。预测控制具备3个基本特征:预测模型、滚动优化、反馈校正[12]。预测控制所需的模型不需要精确的数学模型,只要具备预测功能即可。本文建立的挖泥船横移过程模型能够通过实船之前采集的泥浆浓度与横移速度,预测未来的泥浆浓度,满足预测控制对模型的要求;滚动优化和反馈校正能够使横移控制系统运行时不断进行优化,从而解决挖泥船施工时因外部因素影响无法保持最优的问题。
1 基于RBF-ARX的横移过程模型
在不考虑外界可测干扰的情况下,基于RBF-ARX的绞吸挖泥船横移过程模型如下:
(1)
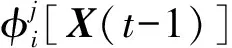
横移过程模型的结构类似线性ARX模型,不同之处是横移过程模型具有函数型系数。横移过程模型通过函数型系数将横移过程的一个个工作点的线性ARX模型进行整合,形成全局非线性模型,模型的函数型系数公式为:
(2)

横移过程模型中的函数型系数依存于状态向量X(t-1),当(t-1)时刻的状态向量确定后,可通过RBF计算获得函数型系数。只要求解出隐含层模型的参数,就能通过RBF神经网络获得函数型系数。本文使用SNPOM参数识别方法求解该函数型系数[14],该方法的核心思想就是将模型参数分为非线性参数和线性参数两类,构建非线性参数子空间和线性参数子空间。非线性参数使用LMM方法优化,线性参数使用LSM方法优化[15]。参数识别过程流程图如图1所示。

图1 横移过程参数识别流程图
从图1可以看出,在进行参数优化之前首先需要确定模型的阶次,模型的阶次通过比较最小信息准则来确定,然后对参数进行分类,分为线性参数和非线性参数,函数型公式中的比例系数与RBF网络中心值为非线性参数,线性权值为线性参数。
2 横移过程控制器设计
2.1 预测控制器结构
建立横移过程模型后,通过预测控制,能够根据控制对象的历史信息假设未来控制输入,从而预测未来信息。横移过程模型能够根据系统已知的过去的泥浆浓度和横移速度,计算出未来的泥浆浓度,然后通过预测控制策略,在浓度设定值的约束下,计算出未来的横移速度。在对未来时刻进行预测控制时,关键是要计算出未来的横移速度。在设计预测控制系统之前,需要对横移过程模型进一步处理,本文将模型转化为状态空间形式,以方便设计控制策略。图2为横移过程预测控制系统结构图,其中yd为浓度设定值,u(k)为控制输入,ym(k)为横移过程模型计算值,y(k)为输出,e(k)为反馈误差。点划线框中为横移过程控制器,通过模型输出与控制系统输出的对比得到反馈误差;将误差反馈给预测输出,再通过在线优化计算得到当前的控制率;然后将控制率输入到控制系统中。如此循环优化,最终得到最佳控制率。

图2 横移过程预测控制系统结构图
2.2 预测控制计算方法
在设计横移过程预测控制策略时,需要将式(1)进行状态空间转化,从而便于运用预测控制理论设计控制策略,简化对控制率的计算。首先,定义状态变量:
(3)
式中:x(t)为状态空间的输入向量;y(t)为输出向量;u(t)为控制向量;a,b为系数。得到横移过程模型的状态空间模型:
(4)
式中:

(5)
式中:N为预测时域;Nu为控制时域。则可以得到控制器的性能优化函数J为:
(6)
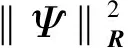
3 控制器参数整定仿真分析
横移过程控制器是否满足要求,取决于其性能指标,选择不同的参数,就可以得到完全不同的控制效果。虽然参数选择的多样性能够增加设计的自由度,但是想要获得好的控制效果,则需要充分分析各个参数对控制系统的影响。为了在设计控制器时减少参数选取的盲目性,本文将讨论参数对系统性能的影响,并使用MATLAB编程,进行仿真分析。
本文预测控制器的预测时域为1,控制时域为1。控制变量u的控制权重R1虽然能够使系统稳定,但会造成静态误差,故选取R1为0。因此主要的调节参数为输出误差权系数Q和横移速度变化量权重R2,Q反映了对不同时刻误差的重视程度,R2对横移速度的变化量加以约束。本节将分3种情况讨论参数Q与R2对系统的影响。
图3分别为无超调、1个超调、多个超调时系统输出泥浆浓度与对应控制率横移速度的对比图。从图3(a)和(b)可以看出,R2不变增大Q和Q不变增大R2均会使系统调节时间变短,而增大Q对系统调节时间的影响较大。从图3(c)和(d)可以看出,当保持R2不变增大Q时,系统的超调量与调节时间变化幅度很小;保持Q不变增大R2时系统的超调量变化明显,调节时间略微变短。从图3(e)和(f)可以看出,当R2不变增大Q时,系统的调节时间几乎不变,超调量略微变小;保持Q不变增大R2时系统的调节时间略微变短,而超调量变化明显。

图3 系统输出泥浆浓度与对应横移速度对比曲线
从上述3种情况的对比可以看出:误差权系数Q小于1时,调节Q,系统反应时间变化明显,当Q大于1时,增大Q系统变化不明显;系统的超调量与控制权系数R2有关,当R2很小时系统无超调,此时系统稳定性较高,但是系统的反应时间较长;随着R2变大,系统开始出现超调,且超调量逐渐变大,系统的输出以及控制器输出开始剧烈变化,系统变得不稳定。
绞吸挖泥船横移控制系统属于慢速变化的控制系统,横移速度变化过快或者变化太剧烈,会使得锚绳拉力变化幅度变大以及频率变化过快,可能导致锚绳寿命变短,甚至在疏浚过程中断裂,发生安全事故,所以选择适当的R2对于系统的稳定性非常重要。通过以上分析,本文选取Q=1、R2=0.5作为横移过程控制器权系数,此时系统输出泥浆浓度与对应控制率横移速度的仿真图如图4所示。

图4 参数整定后泥浆浓度与横移速度仿真图
从图可以看出,泥浆浓度能够在预测控制器的作用下快速达到稳定,且系统反应时间较快,验证了绞吸挖泥船横移过程控制器的合理性。
4 结束语
绞吸挖泥船施工时,土质、地形、船舶作业状态等都具有很大的不确定性,由于这些不确定性,导致所建立的理想模型难以描述横移过程复杂多变的动态特性,并且使得按照理想模型得到的最优控制在实际施工时往往不能保持最优,因此需要一套建模与控制方案,建立横移过程模型描述其动态特性,设计基于该模型的控制器,给出相应的控制策略。本文基于RBF-ARX理论建立横移过程模型,将复杂多变的全局特征通过挖泥船实测数据中每一个采样时刻所对应的工作点的线性ARX模型来描述,并由函数型系数将这些模型整合成一个全局模型。使用预测控制算法设计基于横移过程模型的控制器,通过预测控制的滚动优化和反馈校正的特征,使横移控制系统在疏浚作业时不断地优化校正,从而有效克服挖泥船施工时的诸多不确定性。通过仿真,不断地调节控制器的可调参数误差权系数和控制权系数,获得其对控制系统的影响规律,减少了进一步设计控制器以及应用到实际挖泥船上时在参数调节方面的盲目性。
[1] 倪福生. 国内外疏浚设备发展综述[J]. 河海大学常州分校学报, 2004(1):1-9.
[2] 王艳,谢海英,吴瑛. 国内外疏浚市场现状及发展[J]. 交通部上海船舶运输科学研究所学报, 2004,27(2):109-113.
[3] 唐建中,王庆丰,张麒,等. 绞吸式疏浚作业专家系统理论与实验研究[J]. 中国机械工程,2007(9):2218-2222.
[4] 闭治跃. 挖泥船泥浆管道输送系统效率优化与控制研究[D].杭州:浙江大学, 2008:16-18.
[5] 李志刚. 基于横移阻力的绞吸挖泥船横移自动化设计研究[D].常州:河海大学, 2015:7-8.
[6] 倪福生,赵立娟,齐帜,等. 粗砂水力输送多峰阻力特性[J]. 中国港湾建设, 2010(1):23-27.
[7] 倪福生,赵立娟,顾磊,等. 绞吸挖泥船疏浚仿真研究[J].系统仿真, 2012,24(11):2271-2274.
[8] 朱文亮,倪福生,魏长赟,等. 挖泥船疏浚横移过程线性二次型产量最优控制[J]. 船舶工程, 2016,38(2):24-32.
[9] WU J, PENG H, CHEN Q. RBF-ARX model-based modeling andcontrol of quadrotor[C]//Proceeding of the 2010 IEEE International Conference on Control Aplications (CCA). Yokohama, Japan: IEEE,2010:1731-1736.
[10] INOUSSA G, PENG H, WU J. Nonlinear time series modeling and prediction using functional weights wavelet neural network-based state-dependent AR model[J]. Neurocomputing, 2012,86(1):89-94.
[11] WU J,PENG H, OHTSU K, et al. Ship's tracking control based on nonlinear time series model[J]. Applied Ocean Research, 2012,36:1-11.
[12] 席裕庚. 预测控制[M].北京: 国防工业出版社, 2013:5-9.
[13] 刘璋温. 赤池信息量准则AIC及其意义[J].数学的实践与认识, 1980(3):65-73.
[14] 甘敏,彭辉. 不同基函数对RBF-ARX模型的影响研究[J].中南大学学报, 2010,41(6): 2231-2235.
[15] 甘敏,彭晓燕,彭辉. RBF神经网络参数估计的两种混合优化算法[J]. 控制与决策, 2009,24(8):1172-1176.

